Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

С помощью определителей удобно решать линейные системы линейных алгебраических уравнений (СЛАУ).

Рассмотрим системы линейных алгебраических уравнений с двумя неизвестными:

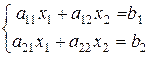                                                                           (3.1)

Решением системы (3.1) называется пара чисел ( 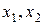), обращающая эту систему в тождество. Если существует только одна такая пара, то решение называется единственным.

Введем обозначения

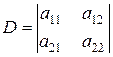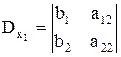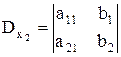, ,         (3.2)

Определитель D, составленный из коэффициентов при неизвестных системы (3.1), называется определителем этой системы. Определитель 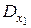получается путем замены первого столбца определителя D свободными членами системы (3.1); определитель  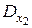получается из определителя D при помощи замены свободными членами системы (3.1) элементов его второго столбца.

Если 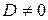, то система (3.1) имеет единственное решение; оно определяется формулами

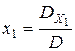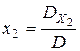,                                                             (3.3)

Такой способ нахождения неизвестных системы двух уравнений первого порядка называется методом Крамера, а формулы (3.3) - формулами Крамера.

Если D = 0 и при этом хотя бы один из определителей 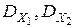отличен от нуля, то система (3.1) совсем не имеет решений (уравнения этой системы несовместны).

Если же D = 0 и также 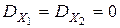, то система (3.1) имеет бесконечно много решений (в этом случае одно из уравнений является следствием другого).

Методом Крамера решаются только системы линейных уравнений, у которых число неизвестных равно числу уравнений.

Пример 1. Решить систему линейных уравнений: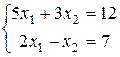

Решение.

Составим определитель системы :

     .

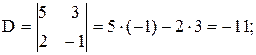
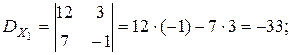
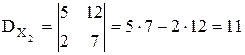D¹0 Þ система имеет единственное решение, определяемое формулами Крамера (3.3):

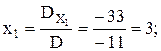
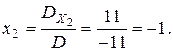
Итак, решение системы: (3; -1).

Пример 2. Решить систему линейных уравнений: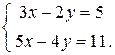

Решение.

Составим определитель системы: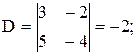

                 

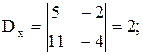
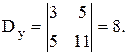
D¹0 Þ система имеет единственное решение, определяемое формулами Крамера (3.3):

                

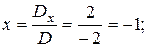
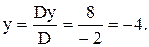
Ответ: (-1; -4).

Пример 3. Решить систему линейных уравнений: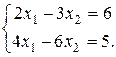

Решение.

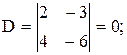
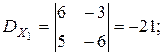
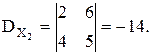
Так как 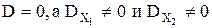, то система не имеет решений (уравнения противоречивы).

Пример 4. Решить систему линейных уравнений: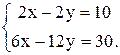

Решение.

             .

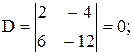
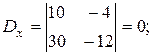
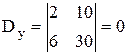Эта система имеет бесконечно много решений (коэффициенты при неизвестных пропорциональны).

С помощью определителей третьего порядка решаются линейные системы трех уравнений с тремя неизвестными:

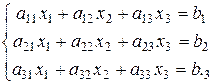                                                           (3.4)

Решением системы (3.4) называется тройка чисел (x₁, x₂, x₃), которая обращает эту систему в тождество.

Решение этой системы можно найти методом Крамера.

Пример 5. Решить систему уравнений методом Крамера.

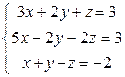
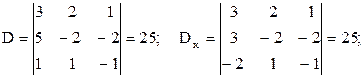Решение.

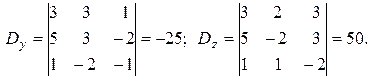
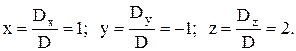
Итак, решением системы является тройка чисел (1; -1; 2).

Замечание: Аналогично методом Крамера решаются линейные системы n-уравнений с n-неизвестными.

Метод Гаусса (метод последовательного исключения неизвестных) состоит в следующем: систему уравнений приводят к эквивалентной ей системе с треугольной матрицей. Эти действия называются прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).

Замечание: системы являются эквивалентными, если множество их решений совпадают.

Рассмотрим метод Гаусса на примере системы трех линейных уравнений с тремя неизвестными.

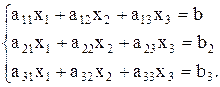                                                          (16.1)

Выпишем матрицу А, составленную из коэффициентов при неизвестных системы:

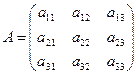                                                                   (16.2)

и расширенную матрицу системы

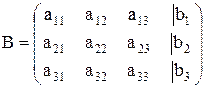.                                                            (16.3)

Теорема Кронекера – Капелли. Cистема линейных уравнений (16.1) совместна тогда и только тогда, если ранг матрицы A равен рангу расширенной матрицы B.

Если этот ранг равен числу неизвестных, то система будет определенной (иметь единственное решение), а если этот ранг меньше числа неизвестных, то система будет неопределенной (иметь бесконечное множество решений).

Пример 1. Решить систему уравнений 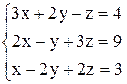 методом Гаусса.

Решение.

Перепишем систему уравнений в таком виде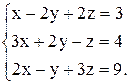

Преобразуем расширенную матрицу системы

~

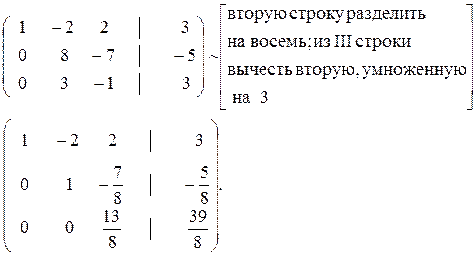
Ранги равны:

rang A = rang B = 3 = количеству неизвестных (по теореме Кронекера- Капелли система совместна и имеет единственное решение).

Запишем новую эквивалентную систему, которой соответствует расширенная матрица системы.

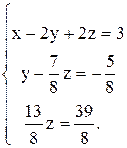
Выполняя обратный ход, с помощью последовательных подстановок находим неизвестные:

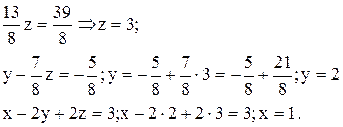
Итак, получаем ответ: (1; 2; 3).

Правильность полученного ответа подтверждается тождеством, которое получается при подстановке полученных результатов в любое из уравнений системы.

Пример 2. Решить систему уравнений методом Гаусса.

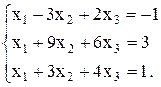
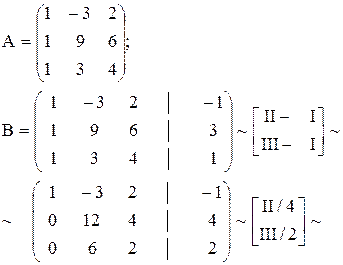Решение. Выпишем матрицу системы, состоящую их коэффициентов при неизвестных

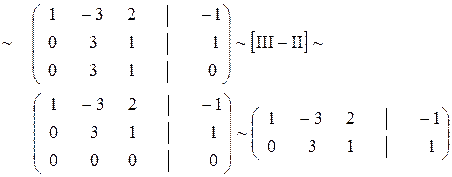
rang A = rang B = 2 < 3 ( количества неизвестных) и по теореме Кронекера-Капелли система совместна и имеет бесконечное множество решений.

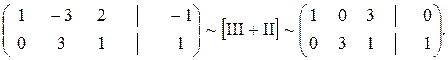
Запишем новую эквивалентную систему, которой соответствует расширенная матрица:

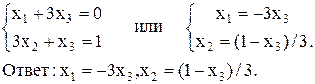
Пример 3. Решить систему уравнений методом Гаусса.

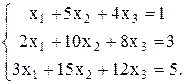
Решение.

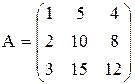
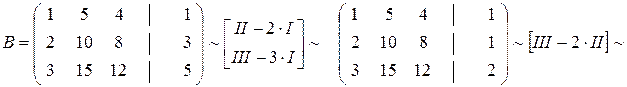
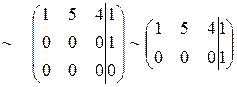      rang B = 2

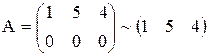rang A=1

rang A¹ rang B - система несовместна, т.е. не имеет решений.