Определители 2-го и 3-го порядка. Правила вычисления определителей.
Определение. Определителем (детерминантом) второго порядка называется выражение
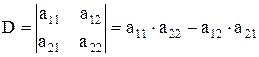
Числа 
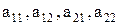 называются элементами определителя; они расположены в двух строках и в двух столбцах (ряды определителя).
называются элементами определителя; они расположены в двух строках и в двух столбцах (ряды определителя).
Говорят, что элементы 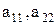 лежат на главной диагонали определителя,
лежат на главной диагонали определителя, 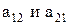 - на побочной.
- на побочной.
Таким образом, определитель второго порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях.
Пример 1. Вычислить 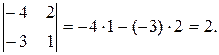
Определение. Определителем (детерминантом) третьего порядка называется выражение
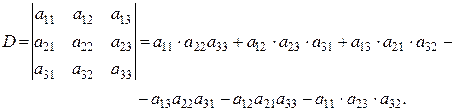
Числа 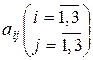 называются элементами определителя; они расположены в его трех строках и трех столбцах. Элементы
называются элементами определителя; они расположены в его трех строках и трех столбцах. Элементы 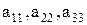 расположены на диагонали определителя, называемой главной; элементы
расположены на диагонали определителя, называемой главной; элементы 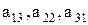 составляют его побочную диагональ.
составляют его побочную диагональ.
Замечание. Первые три слагаемые в правой части равенства (1.2) представляют собой произведения элементов определителя, взятых по три так, как показано различными пунктирами на схеме, приведенной ниже слева.
Чтобы получить следующие три члена правой части равенства (1.2), нужно перемножить элементы определителя по три так, как показано различными пунктирами на этой же схеме справа, после чего у каждого из найденных произведений изменить знак.
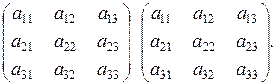
Такой способ вычисления определителей третьего порядка называется правилом "треугольников".
Пример 2. Вычислить определитель третьего порядка.
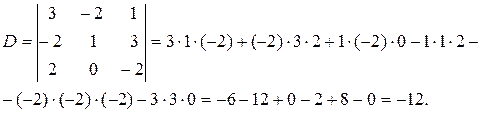
Проиллюстрируем основные свойства определителей, вычисляя определители третьего порядка. Определитель не меняет своего значения, если строки заменить соответствующими столбцами. Такая операция называется транспонированием, т.е.
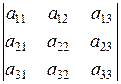 =
= 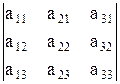
Пример 3. Показать, что 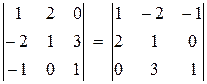 .
.
Посчитаем каждый из определителей.
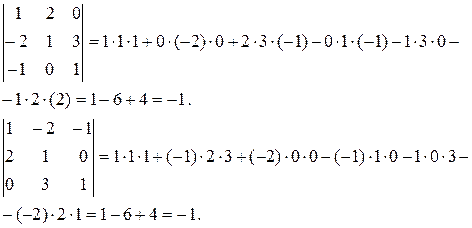
Итак, -1=-1, т.е. определители равны.
II. Определитель, у которого две строки или два столбца одинаковы, равен нулю (D=0).
Пример 4:
а)
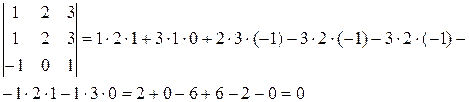
б)
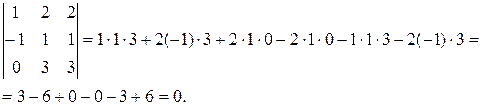
III. При перестановке двух строк (или двух столбцов) определителя его абсолютная величина не изменится, а знак меняется на противоположный.
Пример 5:
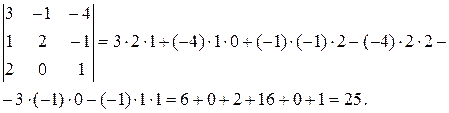
Поменяем местами, например, вторую и третью строки, и посчитаем полученный определитель.
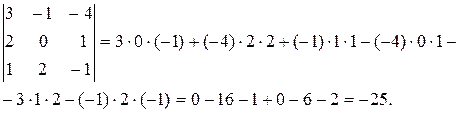
IY. Общий множитель элементов любой строки (столбца) можно выносить за знак определителя.
Пример 6:
Показать, что 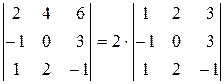
Находим
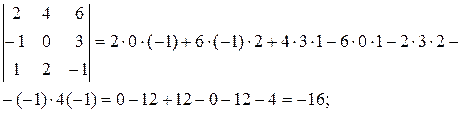
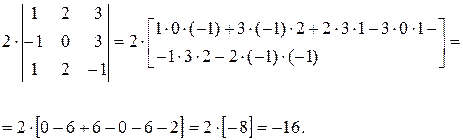
Y. Определитель, у которого две строки (столбца) пропорциональны, равен нулю (следует из IY свойства).
Например, имеем
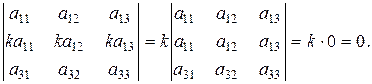
Пример 7:
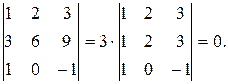
YI. Если все элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель равен сумме двух соответствующих определителей.
Например,
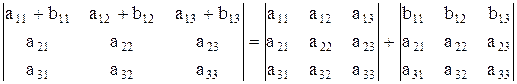 .
.
Пример 8.
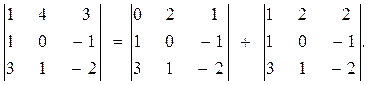 |
Показать, что выполняется данное равенство.
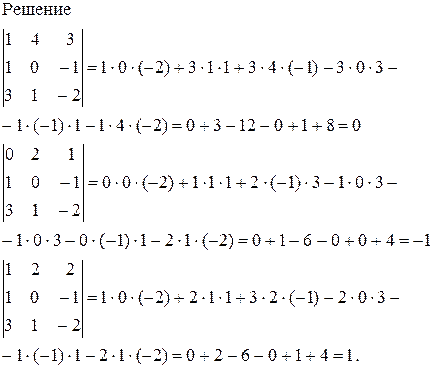
Итак, 0 = -1 + 1
YII. Значение определителя не изменится, если ко всем элементам одной строки (столбца) прибавить (или отнять) соответствующие элементы другой строки (столбца), умноженные на одно и то же число (следует из св-ва YI).
YIII. Треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали - нули, равен произведению элементов главной диагонали
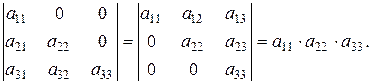
Замечание. Порядок определителей не указывается, так как эти свойства справедливы для определителей любого порядка.
Пример 9.
Вычислить 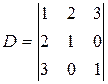 .
.
Решение. Приведем определитель к треугольному виду и вычислим его.
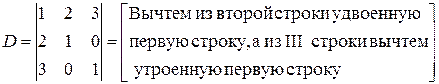
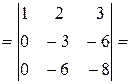 [добавим к 3-й строке вторую строку, умноженную на (-2)]
[добавим к 3-й строке вторую строку, умноженную на (-2)]
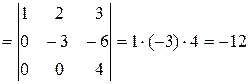 .
.
Дата: 2018-12-28, просмотров: 344.