ДОНЕЦКАЯ НАРОДНАЯ РЕСПУБЛИКА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
КОНСПЕКТ ЛЕКЦИЙ ПО УЧЕБНОЙ
ДИСЦИПЛИНЕ
«ВЫСШАЯ МАТЕМАТИКА»
Специальность: 21.05.04 «Горное дело»
Квалификация: «Горный инженер» (специалист)
Донецк, 2017 г.
СОДЕРЖАНИЕ
Лекция 1. Определители, их свойства и вычисление .............................................
Лекция 2. Решение систем линейных уравнений
(методы Крамера, Гаусса) .......................................................................................
Лекция 3. Матрицы, действия над ними. Матричный метод решения
систем линейных уравнений ...................................................................................
Лекция 4. Векторы, линейные операции над ними, способы задания .................
Лекция 5. Скалярное произведение векторов и его свойства ..............................
Лекция 6. Векторное и смешанное произведение векторов, их
свойства, применение ...............................................................................................
Лекция 7. Линии и их уравнения. Преобразование координат на
плоскости. Полярная система координат ...............................................................
Лекция 8. Уравнение прямой. Основные задачи на прямую .................................
Лекция 9. Линии второго порядка и их свойства ...................................................
Лекция 10. Уравнение плоскости. Основные задачи на плоскость .....................
Лекция 11. Уравнение прямой в пространстве. Взаимное расположение ...........
Лекция 12. Основные задачи на прямую и плоскость ............................................
Лекция 13. Понятие функции, классификация и графики функций ....................
Лекция 14. Последовательности, предел последовательности и
функции, раскрытие неопределенностей ................................................................
Лекция 15. Стандартные пределы. Непрерывность функции ..............................
Лекция 16. Производная, ее вычисление. Касательная и нормаль .......................
Лекция 17. Основные правила дифференцирования .............................................
Лекция 18. Дифференциал функции. Свойства ......................................................
Лекция 19. Основные теоремы дифференциального исчисления .......................
Лекция 20. Возрастание (убывание), экстремумы функций. Необходимые
и достаточные условия экстремума ........................................................................
Лекция 21. Выпуклость, вогнутость. Асимптоты ..................................................
Лекция 22. Полное исследование функций .............................................................
Лекция 23. Функции нескольких переменных (ФНП). Частные
производные, дифференциал ФНП .........................................................................
Лекция 24. Производная по направлению. Градиент. Касательная
плоскость и нормаль .................................................................................................
Лекция 25. Экстремумы ФНП. Наибольшее (наименьшее) значение
ФНП ...........................................................................................................................
Лекция 26. Условный экстремум ФНП ..................................................................
Лекция 26. Первообразная, неопределенный интеграл, его свойства.
Таблица интегралов ..................................................................................................
Лекция 27. Методы интегрирования .......................................................................
Лекция 28. Интегрирование рациональных, иррациональных
и тригонометрических функций ..............................................................................
Лекция 29. Определенный интеграл и его свойства. Формула
Ньютона-Лейбница ...................................................................................................
Лекция 30. Методы интегрирования определенного интеграла ..........................
Лекция 31. Несобственные интегралы. Применение определенного
интеграла ...................................................................................................................
Лекция 32. Двойные интегралы, их свойства и вычисления ................................
Лекция 33. Применение двойных интегралов .......................................................
Лекция 34. Криволинейные интегралы, их вычисления и применение ..............
Лекция 35. Дифференциальные уравнения (ДУ), задача Коши. ДУ
первого порядка ........................................................................................................
Лекция 36. ДУ второго порядка, допускающие понижение .................................
Лекция 37. Определитель Вронского. Формула Лиувиля.
Линейные однородные дифференциальные уравнения второго
порядка с постоянными коэффициентами .............................................................
Лекция 38. Линейные неоднородные дифференциальные уравнения
второго порядка со специальной правой частью. Метод
вариации произвольных констант ...........................................................................
Лекция 39. Числовые ряды, их сходимость. Необходимый и
достаточные признаки сходимости рядов ...............................................................
Лекция 40. Достаточный признаки сходимости знакочередующихся
и знакопеременных рядов ........................................................................................
Лекция 41. Функциональные и степенные ряды. Применение
степенных рядов ........................................................................................................
Лекция 42. Ряды Фурье для периодических и непериодических функций .........
Лекция 43. Ряды Фурье для четных и нечетных функций ...................................
Условия параллельности и перпендикулярности прямых
В пространстве.
Пусть даны две прямые
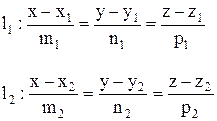 (15.4)
(15.4)
с направляющими векторами 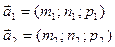 .
.
Если прямые параллельны l1ïïl2, то их направляющие векторы коллинеарны Þ
 . (15.5)
. (15.5)
Если прямые перпендикулярны l1^l2, то их направляющие векторы перпендикулярны, и их скалярное произведение равно нулю:
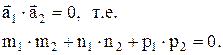 (15.6)
(15.6)
Пример. Через точку А(1; -1; 2) провести прямую, параллельную прямой
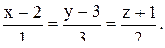
Решение. Напишем уравнения прямой, проходящей через точку А:
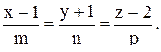
Из условия параллельности двух прямых (15.5) следует, что координаты направляющего вектора этой прямой m, n и p должны быть пропорциональны координатам направляющего вектора данной прямой (1, 3, 2):
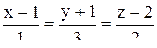 - уравнение искомой прямой.
- уравнение искомой прямой.
Прямая и плоскость.
Лекция 26. Первообразная, неопределенный интеграл, его свойства. Таблица интегралов.
Первообразная функция и неопределенный интеграл
Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Различные вопросы математики, естествознания и техники приводят к решению обратной задачи – восстановлению функции по заданным производной или дифференциалу.
Определение 1. Функция F( x) называется первообразной для функции f(х) на промежутке [a; b], если её производная F'[x) равна f(x) во всех точках этого промежутка, т.е. F'(x) = f(x)
Отыскание по данной функции f(х) её первообразной составляет одну из основных задач интегрального исчисления. Естественно, возникают вопросы: у всякой ли функции существует первообразная и, если существует, то одна или их много?
Ответ на первый вопрос вытекает из утверждения, что всякая непрерывная на [a; b] функция f(x) имеет первообразную.
В дальнейшем изложении, функции, для которых ищутся первообразные, будем считать непрерывными на [a; b], а данные конкретные элементарные функции будем рассматривать только на отрезке их непрерывности.
Ответ на второй вопрос исчерпывается утверждением: если функция f(х) имеет одну первообразную F( x), то она имеет их бесчисленное множество:
Лемма. Функция, производная которой на данном промежутке тождественно равна нулю, постоянна на этом промежутке.
Действительно, пусть для функции 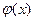 во всех точках
во всех точках  . Тогда для любых х1 и х2: по теореме Лагранжа
. Тогда для любых х1 и х2: по теореме Лагранжа 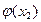 –
–  =
= 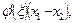 где
где 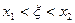 . Так как
. Так как  , то
, то 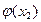 –
–  =0 и
=0 и 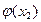 =
=  , т. е. функция, значения которой во всех точках одинаковы, постоянна:
, т. е. функция, значения которой во всех точках одинаковы, постоянна: 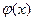 = const.
= const.
Теорема. Если F( x) – первообразная для f(х), то любая другая первообразная для f(х) (на том же промежутке) может быть записана в виде F( x) + С, где С - произвольная константа.
Доказательство.
Пусть Ф(х) произвольная первообразная для f(х) т. к. Ф'(х)= f(х), то для всех точек рассматриваемого промежутка
(Ф(х) – F( x))' =0 (на основании леммы), т. е.
(Ф(х) – F( x))' = Ф'(х) – F'( x) = f(х) – f(х) = 0
Значит, функция Ф(х) – F( x) постоянна на этом промежутке, т. е. |
Ф(х) – F( x) = С
или Ф(х) = F (х) + С.
Определение 2. Если функция F( x) является первообразной для f(х), то совокупность всех первообразных F( x) + С называется неопределенным интегралом от функции f(х):
 ,
,
где 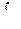 –- знак интеграла;
–- знак интеграла;
f(х) – подынтегральная функция,
f(х) dx – подынтегральное выражение
 Геометрически: если у =
Геометрически: если у = 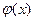 и у = F( x)
и у = F( x)
первообразные для f(х), то касательные
к их графикам в точках с общей
абсциссой х параллельны между собой
tg(α) = F'{x) = Ф'(х)
В таком случае расстояние между этими
кривыми, считая вдоль оси ОУ, остается
постоянным: Ф(х) – F( x))= С, т. е. эти кривые идут в некотором смысле "параллельно" друг другу.
Отыскание первообразной и отыскание неопределенного интеграла от функции называется интегрированием этой функция. Чтобы проверить правильность интегрирования достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Основные свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
3. Неопределенный интеграл от производной равен самой функции плюс произвольная константа

4. Неопределенный интеграл от дифференциала равен дифференцируемой функции плюс константа

5. Постоянный множитель можно выносить за знак интеграла

6. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен сумме интегралов от этих функций (если они существуют)

При вычислении неопределенных интегралов полезно иметь в виду следующие правила:
1. Если  , то
, то 
2. Если  , то
, то 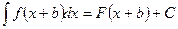
3.  Если
Если  , то
, то 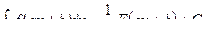
Основная таблица интегралов
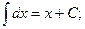
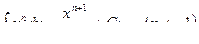
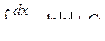




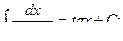

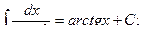

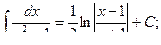
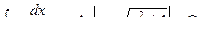

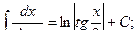
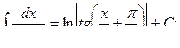

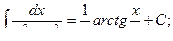
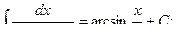
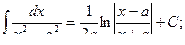
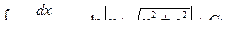
Пример 1

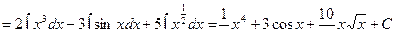
Здесь применили основные свойства интегралов и таблицу интегралов, выполнили непосредственное интегрирование.
Теорема 4.
 ( * )
( * )
где Q( x) – многочлен с неопределенными коэффициентами, степень которого ниже степени многочлена P( x);
λ– произвольная константа;
При вычислении указанного вида интегралов применяется
метод неопределенных коэффициентов
Для нахождения неопределенных коэффициентов
дифференцируют обе части равенства (*), затем умножают на 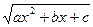 и, сравнивая коэффициенты при одинаковых степенях х, определяют λ и коэффициенты многочлена Q(x).
и, сравнивая коэффициенты при одинаковых степенях х, определяют λ и коэффициенты многочлена Q(x).
Замечание. Формулу (*) применяют тогда, когда степень многочлена Р(х)больше единицы.
 Пример 27.
Пример 27.
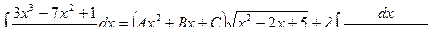
Продифференцируем это равенство:

Приведем к общему знаменателю и перемножим:
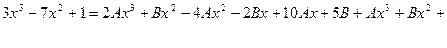
Найдем коэффициенты с помощью метода неопределенных коэффициентов:
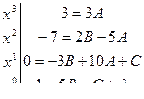
A = 1, B = -1, C = -13, λ = -7
Подставим найденные значения коэффициентов и получим интеграл от элементарной функции

Пример 28
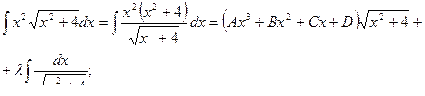
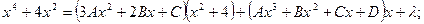

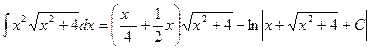
Пример 29
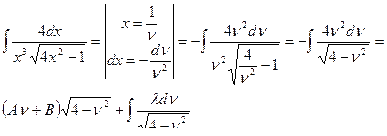
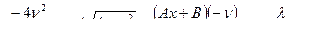

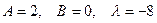

Теорема 5. Интеграл вида 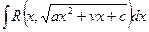 с помощью
с помощью
подстановок Эйлера приводится к интегралу от рациональной
функции.
Подстановка Эйлера:
1. Если а > 0 , то используется подстановка
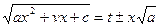
2. Если а < 0, с>0, то используется подстановка
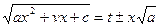
3. Если а < 0, а. подкоренное выражение раскладывается на действительные множители 
 , то используется подстановка
, то используется подстановка 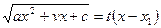
Пример 30
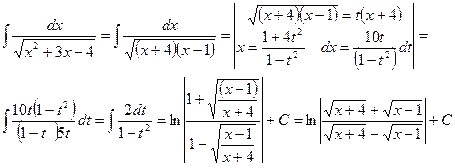
Интегрирование дифференциальных биномов.
Дифференциальным биномом называется выражение xm (а + bх n) p dx, где m, n, p – рациональные числа.
Теорема. Интеграл от дифференциального бинома 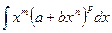 приводится к интегралу от рациональной функции лишь в трех случаях:
приводится к интегралу от рациональной функции лишь в трех случаях:
1) р – целое число, то с помощью подстановки 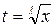 ,
,
где λ – общий знаменатель m и n
2)  целое число, то с помощью подстановки
целое число, то с помощью подстановки
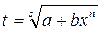 , где s - знаменатель р;
, где s - знаменатель р;
3) 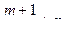 – целое число, то с помощью подстановки
– целое число, то с помощью подстановки
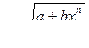 , где s – знаменатель р.
, где s – знаменатель р.
Академик П.Л.Чебышев (1821-1894) доказал: что во всех остальных случаях интеграл от дифференциального бинома через элементарные функции не выражается.
Пример 31.
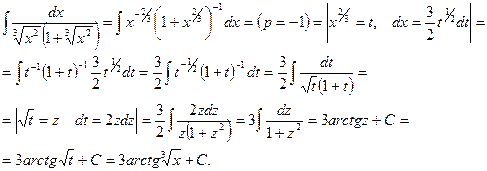
Пример 32
 .
.
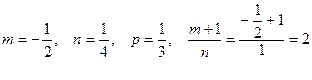
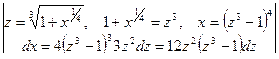 – подстановка
– подстановка
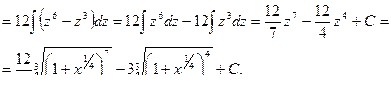
Интегрирование тригонометрических функций.
Переходя к рассмотрению приемов интегрирования тригонометрических выражений, предварительно заметим, что любая тригонометрическая функция рационально выражается через тангенс половинного угла:
 ( 1 )
( 1 )
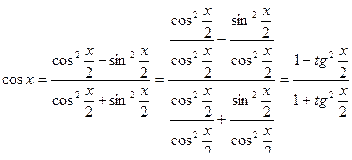 ( 2 )
( 2 )
а так как tgx, ctgx, secx, cosecx рационально выражаются через
sinx и cosx , то они рационально будут выражаться и через 
Теорема 1. Интеграл вида 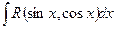 подстановкой
подстановкой 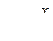
приводится к интегралу от рациональной функции t, который, как было указано выше, всегда выражается в элементарных функциях.
Действительно, пусть 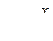 , тогда на основании (1), (2)
, тогда на основании (1), (2)
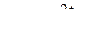
Определим x и dx, найдем, что 
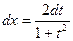
В подынтегральное выражение вместо sinx, cosx и dx подставим их значения
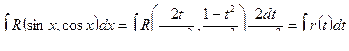 ,
,
где r(t) - рациональная функция t.
Так как подстановкой  интеграл от любой рациональной
интеграл от любой рациональной
относительно sinx и cosx, тригонометрической функции приводится к
интегралу от рациональной функции , то подстановка  называется универсальной.
называется универсальной.
Пример 33.

Замечание. Универсальная подстановка всегда приводит к цели, однако часто она приводит к громоздким выкладкам
Рассмотрим другие подстановки, которые в частных случаях быстрее приводят к цели.
Теорема 2. Если функция R(sinx, cosx) нечетна относительно cosx , то интеграл  подстановкой t = sinx приводится к интегралу от рациональной функции.
подстановкой t = sinx приводится к интегралу от рациональной функции.
Действительно, преобразуем интеграл
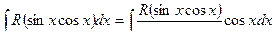
Так как R(sinx,cosx) нечетна относительно cosx и может содержать cosx лишь в четных степенях. Следовательно, это выражение является рациональной функцией относительно sinx:
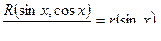 то есть
то есть
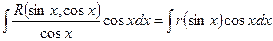
К последнему интегралу применим подстановку t = sinx, тогда dt=cosxdx:
 =
= 
Таким образом, указанная подстановка привела данный интеграл к интегралу от рациональной функции относительно t.
Пример 34.
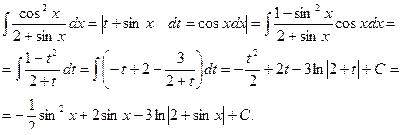
Теорема 3. Если функция R(sinx,cosx) нечетна относительно sinx ,то подстановкой t = cosx интеграл  риводится к интегралу от рациональной функции.
риводится к интегралу от рациональной функции.
Пример 35.
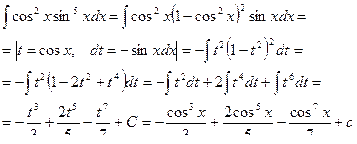
Пример 36.
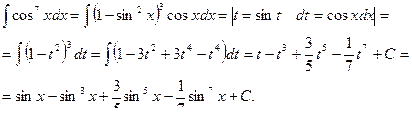
Замечание. Теоремы 2 и 3 применяются при интегрировании произведения sinm cos n x натуральных степеней cosx и sinx, когда хотя бы одно из чисел m и n - нечетное.
Теорема 4. Если функция R(sinx,cosx) имеет четный характер
относительно sinx и cosx . то интеграл 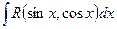
подстановкой t = tgx приводится к интегралу от рациональной функции.
Преобразуем подынтегральную функцию:
R(sinx,cosx) = R(tgx cosx, cosx)
Правая часть этого равенства имея четный характер относительно cosx, может содержать лишь четные степени cosx , а т. к.
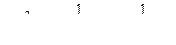
то вся подынтегральная функция является некоторой рациональной функцией от tgx, т.е. R(sinx,cosx)=r(tgx).
Умножим и разделим r(tgx) на sec2x и затем применим подстановку
t = tgx, dt = sec2xdx
Получим

Заметим также, что cos2 x и sin 2 x могут быть рационально выражены через tg2x:
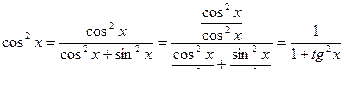
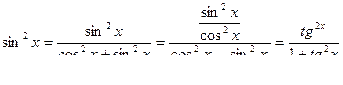
Пример 37.
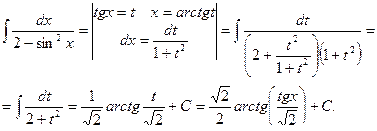
Теорема 5. Если подынтегральная функция представлена в виде произведения неотрицательных степеней sinx и cosx, то интегрирование таких функций производят заменяя четные степени sinx и cosx синусами и косинусами кратных аргументов, используя при этом известные формулы тригонометрии
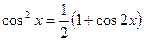
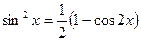

Пример 38.
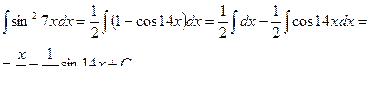
Пример 39.

Пример 40.
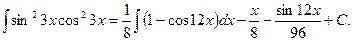
Примечание 1. Для интегралов от целых, больших единицы, степеней tgx, сtgx и от положительных четных степеней secx и cosecx
удобнее использовать соотношения:


Пример 41.

Пример 42.
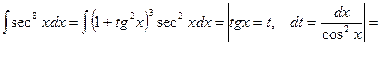
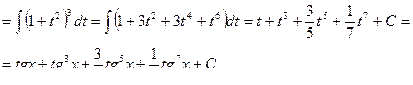
Примечание 2. Интегралы произведения синусов и косинусов различных аргументов приводятся к табличным интегралам с помощью тригонометрических формул:
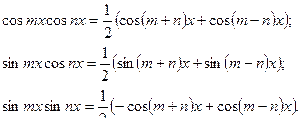
То есть

Пример 43.
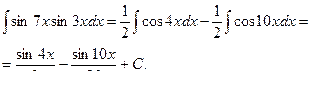
Пример 44.

Интегрирование иррациональных функций с помощью тригонометрических подстановок
Квадратный трехчлен, стоящий под знаком интеграла, путем выделения полного квадрата и замены переменных может быть представлен в форме двучлена 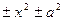 и тогда интеграл вида
и тогда интеграл вида
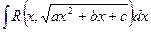
где R(...) – рациональная функция, всегда можно свести к одному из интегралов следующих типов:
1. 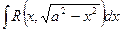
2. 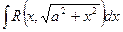
3. 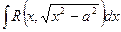
. 4. Четвертая комбинация знаков (- x2-а2) приводит нас к
подынтегральной функции, которая не существует в действительной области.
Теорема 1. Интеграл вида 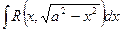 подстановкой х=а sint (х=а cost) сводится к интегралу от рациональной функции относительно sint и cost.
подстановкой х=а sint (х=а cost) сводится к интегралу от рациональной функции относительно sint и cost.
. Действительно, пусть х=а sint, тогда dx = a cost dt, 
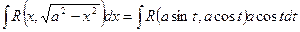
Пример 45.

Теорема 2. Интеграл вида 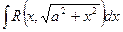 подстановкой
подстановкой
x=a tgt сводится к интегралу от рациональной функции относительно tgt и sect.
Действительно, пусть x=a tgt, тогда dx=a sec2tdt, 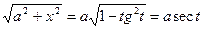
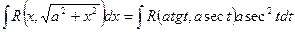
Пример 46.
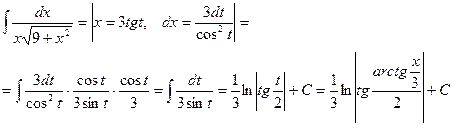
Теорема 3. Интеграл вида 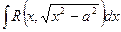 подстановкой
подстановкой
x=a seсt сводится к интегралу от рациональной функции относительно tgt и sect.
Действительно, пусть x=a sect, тогда dx=a tgt sect dt, 
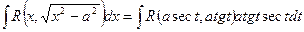
Пример 47.


Пример 48
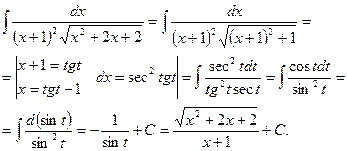
Понятие о “неберущихся” интегралах
Теорема существования неопределенного интеграла утверждает, что всякая непрерывная на интервале (а, b) функция f(x) имеет на этом интервале первообразную F(x). Эта теорема вовсе не утверждает: что первообразную данной функции можно фактически отыскать с помощью конечного числа известных операций и выразить ответ в элементарных функциях (алгебраических, показательных, тригонометрических и т.п.). Более того, имеются такие элементарные функции, интегралы от которых не выражаются через элементарные функции.
Так, например, мы уже указывали, что первообразные от дифференциальных биномов, не принадлежащие к трем рассмотренным видам (условия Чебышева), не выражаются через элементарные функции в конечном виде.
Такие интегралы называют “неберущимися”, подразумевая под этим, что такого рода интегралы не могут быть выражены с помощью конечного числа элементарных функций.
Интегралы вида
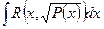 ,
,
где Р(х) – многочлен степени выше второй, в общем случае не выражается через элементарные функции. При этом, если Р(х) - многочлен третьей или четвертой степени, то такие интегралы
называются эллиптическими, если же степени выше четвертой, то ультраэллиптическими.
В некоторых случаях 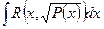 могут выражаться и через элементарные функции, имеющие большое прикладное значение; следует. указать интеграл Пуассона:
могут выражаться и через элементарные функции, имеющие большое прикладное значение; следует. указать интеграл Пуассона: 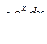 ; интегральный синус
; интегральный синус 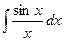 ; интегральный косинус
; интегральный косинус 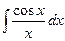 ; интегралы Френеля
; интегралы Френеля 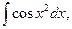
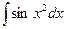 .Указанные интегралы существуют, но наших средств недостаточно, чтобы составить из них конечные выражения для этих интегралов.
.Указанные интегралы существуют, но наших средств недостаточно, чтобы составить из них конечные выражения для этих интегралов.
Свойства двойного интеграла
1.  не зависит от обозначения переменных интегрирования
не зависит от обозначения переменных интегрирования
2. Постоянный множитель k можно выносить за знак двойного интеграла:
или
если k – произвольное число , и f( x, y) интегрируема в области s, то kf( x, y) также интегрируема.
3. Двойной интеграл суммы (разности) конечного числа слагаемых равен сумме (разности) двойных интегралов:
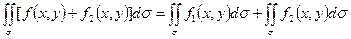
или
если f1( x, y) и f2( x, y) в области s, то их сумма (разность) также интегрируема в области s.
Совокупность свойств 2 и 3 называется линейностью интеграла.
4. Если область s разбита на любое число областей D s1, D s2 … D sт, не имеющих общих внутренних точек и в каждой из этих областей функция f( x, y) интегрируема, то
 |
Это свойство называется аддитивностью интеграла
5. Если всюду в области s функция ¦(x,y) положительная, то и двойной интеграл этой функции по области s будет положительным
6. Если всюду в области s функции ¦1 (x,y) и ¦2 (x,y) интегрируемы и
¦1 (x,y) 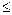 ¦2 (x,y), то:
¦2 (x,y), то:
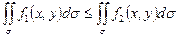
Это свойство называется монотонностью интеграла.
7. Если ¦ (x,y) интегрируема в области s, то функция |¦ (x,y)| также интегрируема и
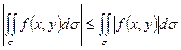
Оценка интеграла по модулю.
8. Если ¦ (x,y)  1, то
1, то
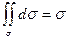
Доказательство:
Так как в данном случае ¦(x,y,z)=1 в области s, то для любого разбиения
области s на части Ds1,Ds2 …Dsn получим:


 |
9. Теорема о среднем
Если функция непрерывна в замкнутой области s, то в этой области существует точка P( x, h) такая, что

|
|
Пусть m – наименьшее значение функции f( x, y) в замкнутой области s;
М – наибольшее значение функции f( x, y) в замкнутой области s;
тогда для любой точки (x,y) этой области, значения функции удовлетворяют неравенствам:
m £ ¦(x,y) £M
Проинтегрируем это неравенство и применим свойства 6, 2, 8:
 |
То есть
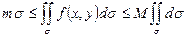 или
или
Функция ¦(x,y) непрерывна в замкнутой области s, принимает все промежуточные значения между своими наименьшим и наибольшим значениями. Следовательно, существует в области s точка Р(x,h) такая, что
 |
или, что то же
 |
ДОНЕЦКАЯ НАРОДНАЯ РЕСПУБЛИКА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
КОНСПЕКТ ЛЕКЦИЙ ПО УЧЕБНОЙ
ДИСЦИПЛИНЕ
«ВЫСШАЯ МАТЕМАТИКА»
Дата: 2018-12-28, просмотров: 395.