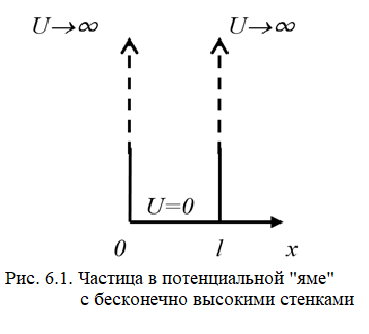
Рассмотрим поведение частицы, в потенциальном поле, показанном на рис.6.1.

 Для простоты рассмотрим одномерный случай, когда частица движется вдоль оси Ox. Такая «яма» описывается потенциальной энергией:

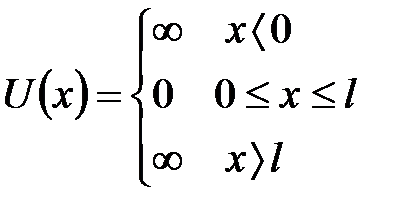
где l – ширина ямы, а энергия отсчитывается от ее дна.

Запишем уравнение Шредингера для стационарных состояний в случае одномерной задачи:

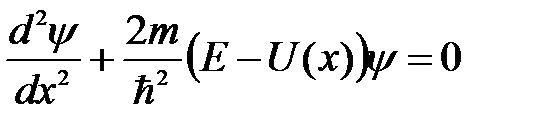                         (6.16)

По условию задачи (яма имеет бесконечно высокие «стенки») частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения, а, следовательно, и волновая функция, за пределами ямы равны нулю. На границах «ямы» (x = l и x = 0) волновая функция, вследствие непрерывности, также должна обращаться в нуль. Следовательно, граничные условия принимают вид:

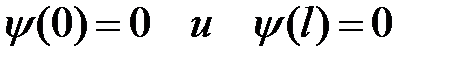.                                              (6.17)

Тогда в пределах ямы уравнение (6.16) сведется к уравнению

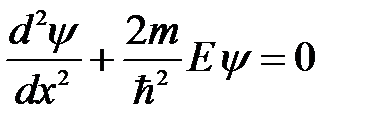,                                                                        (6.18)

или

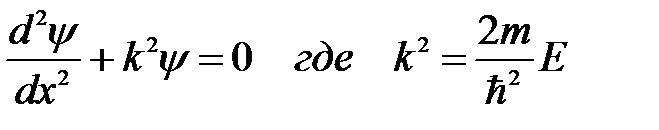.                       (6.19)

Общее решение уравнения (6.19) запишем в виде:

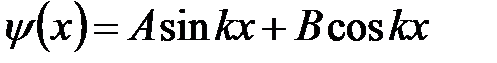.           (6.20)

Используя первое граничное условие из (6.17), получим В = 0, тогда решение (6.20) принимает вид:

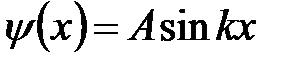.                                                                (6.21)

Используя второе граничное условие из (6.17), получаем, что kl = n p , где n – целое число, следовательно,

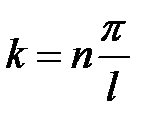.                                                                                (6.22)

Условие (6.22) имеет простой физический смысл. Так как волновое число связано с длиной волны

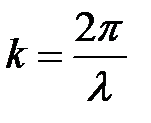,                                            (6.23)

где l – длина волны де Бройля для микрочастицы, то приравняв правые части (6.22) и (6.23), получим:

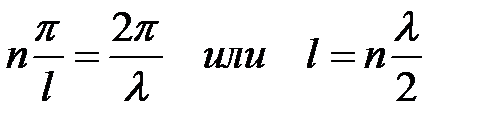.                   (6.24)

Следовательно, на длине ямы ( l ) должно укладываться целое число длин полуволн ( l /2 ), т.е., образуется стоячая волна, причем возможные длины волн l _n принимают дискретный ряд значений. Из уравнений (6.14) и (6.23) следует, что энергия частицы в потенциальной «яме» равна:

.               (6.25)

Из уравнения (6.25) следует, что энергия частицы в потенциальной яме не может быть любой. Она принимает лишь ряд дискретных собственных значений Е _n . Другие значения энергии невозможны. Физические величины, которые могут принимать лишь определенные дискретные значения, называются квантованными. Следовательно, энергия частицы в потенциальной яме квантована.

Квантованные значения энергии называются уровнями энергии, а числа n, которые определяют энергетические уровни частицы, называются квантовыми числами. Таким образом, частица в потенциальной яме может находиться на определенном энергетическом уровне, иногда говорят, в определенном квантовом состоянии n.

Интервал между соседними энергетическими уровнями равен

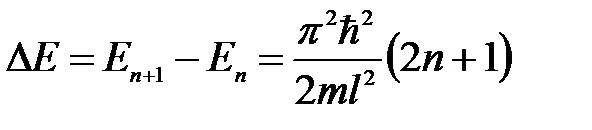.                            (6.26)

Для «ямы», размеры которой соизмеримы с размерами атома (l = 10^{-9 м),}

,

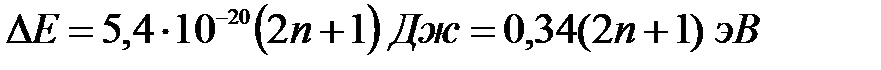Для «ямы» макроскопических размеров (l = 10² м)

.

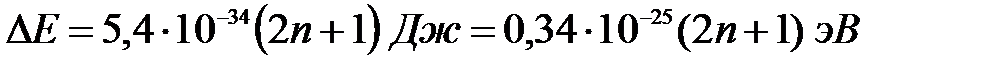В последнем случае энергетические уровни расположены так тесно, что их можно считать квазинепрерывными. Для такой потенциальной «ямы» квантование энергии дает результаты, мало отличающиеся от результатов классической физики. Отметим, что D Е → 0 при l ® ¥ , т.е., энергетический спектр свободной частицы будет непрерывным.

Квантово-механическое решение данной задачи приводит к выводу, что частица в потенциальной «яме» не может иметь энергию, меньшую, чем минимальная энергия, равная

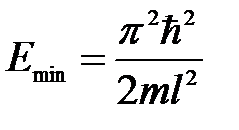.                                          (6.27)

Рассмотрим влияние квантового числа n на характер расположения энергетических уровней частицы в потенциальном «ящике». Сравним интервал между соседними энергетическими уровнями с энергией частицы, находящейся на n-м уровне, используя соотношения (6.26) и (6.27):

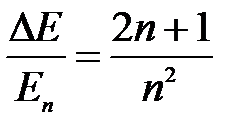.                                                  (6.28)

Тогда для больших квантовых чисел n >> 1 (т.е. 2 n +1 ≈ 2 n ) получим:

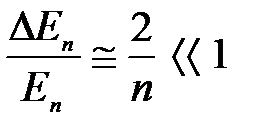,                                                   (6.29)

т.е., соседние уровни расположены тем теснее, чем больше n. Этот результат является частным случаем принципа соответствия Бора – при больших значениях квантовых чисел законы квантовой механики должны переходить в законы классической физики. Например, согласно гипотезе де Бройля, волновые свойства присущи всем телам, однако в случае макроскопического тела волновыми свойствами можно пренебречь, т.е., применять классическую механику Ньютона.

Запишем собственные y -функции, подставив в уравнение (6.21) значения k (6.23):

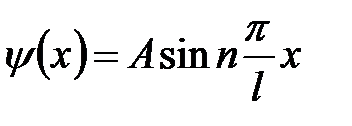.                                             (6.30)

Постоянную A найдем из условия нормировки:

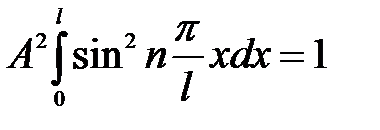.                                           (6.31)

Решая уравнение (6.31) относительно A , получим:

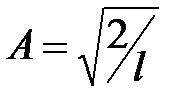.                                                           (6.32)

Окончательно, собственные y -функции будут иметь вид:

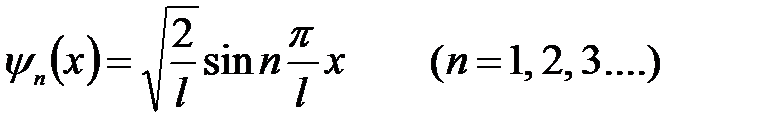.                                   (6.33)

На рис.6.2 представлено поведение собственных функций y _n ( x ) и плотности вероятности обнаружения частицы | y _n ( x ) | ² в различных точках “ямы” для трех энергетических уровней при n = 1, 2, 3:

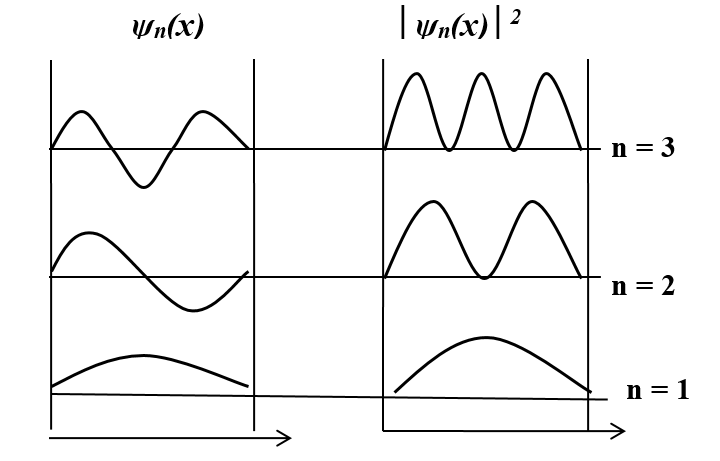
Рис.6.2. Собственные функции y _n ( x ) и плотность вероятности обнаружения частицы | y _n ( x ) | ² в различных точках “ямы”

Из рис.6.2 следует, что в квантовом состоянии при n = 2 частица не может находиться в середине ямы, но одинаково часто может встретиться в точках с координатами 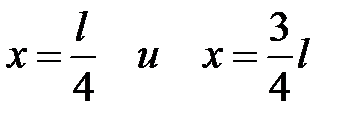, что еще раз свидетельствует, о несостоятельности представлений о траекториях частицы в квантовой механике.