Волны де Бройля, связанные с движущимися частицами, имеют специфическую квантовую природу, не имеющую аналогии в классической физике.

Из опытов по дифракции электронов обнаруживается неодинаковое распределение пучков электронов, отраженных или рассеянных по различным направлениям – в некоторых направлениях наблюдается большее количество электронов, т.е. вероятность попадания электронов в различные точки экрана наблюдения неодинакова. С волновой точки зрения это соответствует большей интенсивности волн де Бройля в этих направлениях. Другими словами, интенсивность волн в данной точке пространства определяет число электронов, попавших в эту точку за 1 с. Это послужило основанием для статистического, вероятностного истолкования волн де Бройля.

Квадрат модуля амплитуды волны де Бройля в данной точке пространства является мерой вероятности того, что частица обнаруживается в этой точке

ê A ê ² ~ W .                                                (6.1)

Для описания распределения вероятности нахождения частицы в данный момент времени в некоторой области пространства вводится волновая функция y ( x , y , z , t ), определяемая следующим образом: вероятность (dW) того, что частица находится в элементе объема (dV) пропорциональна квадрату модуля волновой функции | y | ² и элементу объема (dV):

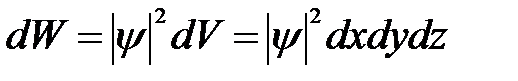                          (6.2)

где 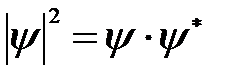, y^* - функция, комплексно сопряженная с y .

Величина | y | ²  имеет смысл плотности вероятности:

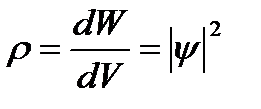,                                           (6.3)

то есть, определяет вероятность нахождения частицы в данной точке пространства. Иными словами | y | ²  определяет интенсивность волн де Бройля. Таким образом, физический смысл имеет не сама y - функция, а квадрат ее модуля | y | ² .

Вероятность обнаружения микрочастицы в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна:

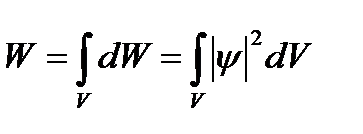                        (6.4)

Волновая функция должна удовлетворять условию нормировки:

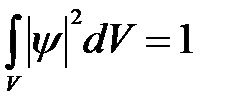.                                                  (6.5)

Уравнение (6.5) означает, что нормировать y - функцию следует таким образом, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это условие говорит об объективном существовании частицы во времени и пространстве. Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять ряду требований, а именно:

y - функция должна быть:

1) конечной, так как вероятность не может быть больше единицы;

2) однозначной, так как вероятность не может быть многозначной величиной;

3) непрерывной, так как вероятность не может изменяться скачками.

Волновая функция удовлетворяет суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями y ₁, y _2, y _3,….. y _{n ,}  то она может находиться в состоянии y , описываемом линейной комбинацией этих функций

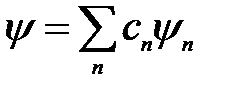.                                                 (6.6)

Знание волновой y - функции позволяет в квантовой механике вычислять средние значения физических величин.

Уравнение Шредингера

В классической физике второй закон Ньютона позволяет решать основную задачу – по заданным силам, действующим на тело, и по начальным условиям определить в любой момент времени координаты тела, его скорость, т.е., описать движение тела в пространстве и во времени. В квантовой механике необходимо учесть двойственную природу микрочастиц, которая ограничивает возможность применения к таким частицам классических понятий о координате и скорости. Это уравнение должно быть таким, чтобы позволяло учесть волновые свойства частиц. Поскольку положение частицы в пространстве задается в квантовой механике через волновую функцию y (x , y . z . t), то основное уравнение квантовой механики должно быть уравнением относительно функции y (x,y.z.t). Это уравнение должно быть волновым, ибо из него должны получить свое объяснение опыты по дифракции микрочастиц.

Основное уравнение квантовой механики было найдено в 1926 году Э.Шредингером. Как и законы Ньютоны, уравнение Шредингера не выводится, а постулируется. Справедливость данного уравнения подтверждается тем, что выводы квантовой механики, полученные с его помощью в атомной и ядерной физике, находятся в хорошем согласии с опытом. Уравнение Шредингера имеет вид:

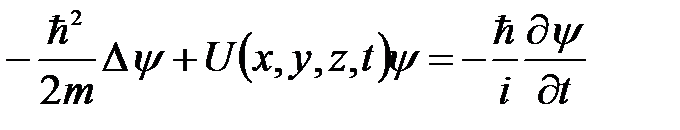,                     (6.7)

где m – масса частицы; U ( x , y , z , t ) – потенциальная энергия частицы в силовом поле, где она движется; 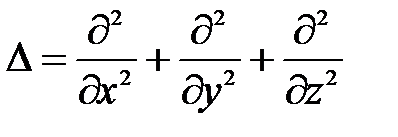 - оператор Лапласа, y = y ( x , y , z , t ) - искомая волновая функция.

Уравнение (6.7) называют временным или общим уравнением Шредингера. Оно справедливо для любой частицы с массой m, которая движется со скоростью V << c. Решение уравнения (6.7) можно представить в виде:

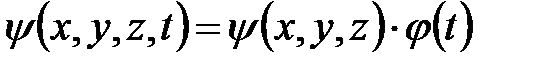,                     (6.8)

где y (x,y,z) - координатная или амплитудная часть волновой функции; j ( t ) - временная часть волновой функции.

При решении ряда физических задач микромира необходимо уметь находить стационарные, т.е., не содержащие времени, решения уравнения Шредингера. Это имеет смысл в тех случаях, когда потенциальная энергия частицы не зависит от времени U = U ( x , y , z ). Решением в этом случае будет волновая функция вида y =y(x, y, z), т.е. ее амплитудная часть. Уравнение Шредингера, соответствующее этому решению, принимает вид

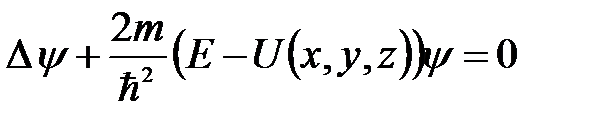,                                                        (6.9)

где m – масса частицы; Е –полная энергия частицы; D - оператор Лапласа.

Это уравнение называется стационарным уравнением Шредингера.

Волновые функции y =y(x,y,z,t), удовлетворяющие уравнению Шредингера при данном U = U ( x , y , z ), называют собственными функциями. Значения полной энергии (Е), при которых существуют решения уравнения Шредингера (6.9), называются собственными значениями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае будет присутствовать сплошной спектр энергий, а во втором – дискретный.

Движение свободной частицы

Свободная частица – это частица, движущаяся в отсутствие внешних полей. Рассмотрим частицу, которая движется вдоль оси Ох, то есть, будем решать одномерную задачу. Поскольку частица свободная, на нее не действуют силы и ее потенциальная энергия U ( x ) = const. Положим U ( x ) равной нулю. Тогда полная энергия этой частицы совпадает с кинетической и стационарное уравнение Шредингера (6.9) принимает вид:

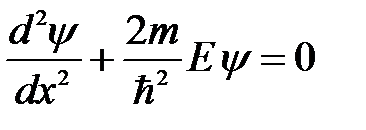;                                       (6.10)

если ввести обозначение

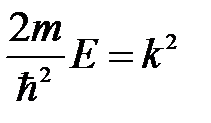,                                               (6.11)

то уравнение (6.10) можно записать в виде:

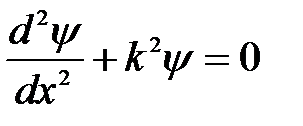.                                           (6.12)

Решение уравнения (6.12) имеет вид

y ( x ) = A × e^ikx,                                             (6.13)

где A = const и k = с onst .

Собственные значения энергии получим из (6.11):

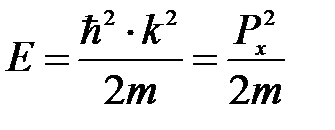.                                                                         (6.14)

Зависимость энергии от импульса частицы имеет вид, типичный для нерелятивистской частицы. Следовательно, энергия свободной частицы (Е), как и волновое число (k), может принимать любые значения, т.е., ее энергетический спектр является непрерывным. Таким образом, свободная микрочастица описывается плоской монохроматической волной де Бройля. Этому соответствует плотность вероятности обнаружения частицы в данной точке пространства, которая не зависит от времени:

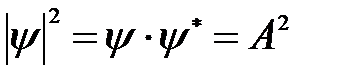,                                       (6.15)

т.е. все положения частицы в пространстве равновероятны.