Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера
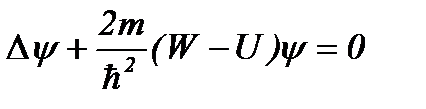, (8.1)
где D - оператор Лапласа (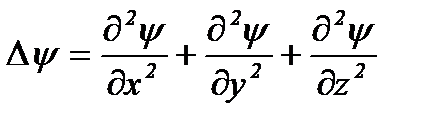 
), m – масса электрона, 
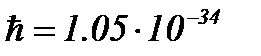Дж∙с – постоянная Планка, Е – полная энергия электрона, U – потенциальная энергия частицы в силовом поле, в котором она движется.
Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze ( Z = 1 для атома водорода), равна:
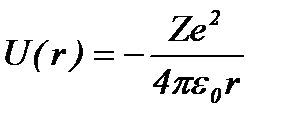, (8.2)
где r – расстояние между электроном и ядром.
Таким образом, стационарное уравнение Шредингера для электрона в атоме водорода записывается следующим образом:
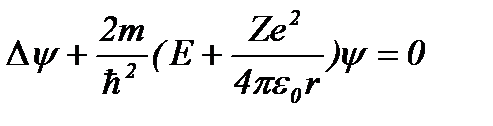. (8.3)
Это уравнение имеет решение, удовлетворяющее требованиям однозначности, конечности и непрерывности волновой функции y , только при собственных значениях энергии
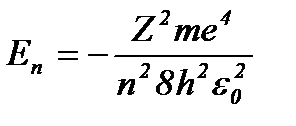, ( n = 1, 2, 3,... (8.4)
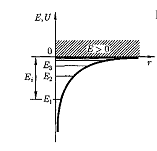Таким образом, решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Уравнение (8.4) совпадает с формулой, полученной Бором для энергии атома водорода. Возможные значения Е1, Е2, Е3… представлены на рис.8.1. в виде горизонтальных прямых.
Как и в теории Бора, самый нижний уровень Е1, соответствующий минимально возможной энергии, называется основным, все остальные - возбужденными. При Е < 0 электрон находится внутри гиперболической «потенциальной ямы», движение электрона является связанным. При n ® ∞ En ® 0, а при Е > 0 движение электрона является свободным. Область непрерывного спектра E > 0 соответствует ионизированному атому.
Рис.8.1. Энергетические уровни
в атоме водорода
Энергия ионизации атома водорода равна:
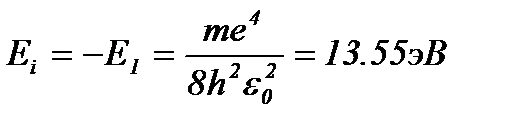. (8.5)
В отличие от теории Бора, в квантовой механике уравнению Шредингера удовлетворяют собственные функции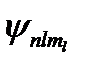 
, определяемые тремя квантовыми числами: главным n, орбитальным l и магнитным ml.
Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы: n = 1, 2, 3,…
Орбитальное квантовое число l определяет момент импульса электрона в атоме:
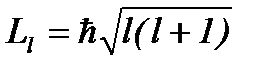(8.6)
При заданном значении главного квантового числа n орбитальное квантовое число принимает значения l = 0, 1, 2, …, ( n -1), т.е., всего n значений.
Магнитное квантовое число определяет проекцию момента импульса электрона на направление z внешнего магнитного поля:
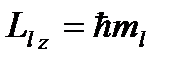. (8.7)
При заданном значении l магнитное квантовое число может принимать значения: ml = ± 1, ± 2, ….., ± l , то есть, всего (2 l + 1) значений. Это означает, что вектор момента импульса может иметь в пространстве 2 l +1 ориентаций.
Таким образом, число различных состояний, соответствующих данному n, равно:
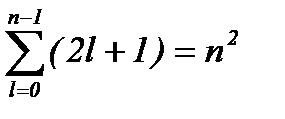(8.8)
Каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема, которая неодинакова в различных частях атома. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в разных точках объема атома. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml – ориентацию электронного облака в пространстве.
Состояние электрона, характеризующееся квантовыми числами l = 0, называют s – состоянием, l = 1 – p – состоянием, l = 2 – d- состоянием, l = 3 – f -состоянием, l = 4 – g-состоянием и т.д.
Квантовые числа n , l и ml позволяют более полно описать спектр поглощения и испускания атома водорода, полученный в теории Бора
В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света:
1. Изменение орбитального квантового числа l удовлетворяет условию: D l = ± 1.
2. Изменение орбитального квантового числа l удовлетворяет условию: D ml = 0, ± 1.
Экспериментальные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) дополнительной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме, наряду с указанными выше тремя квантовыми числами, необходимо задавать еще одно – магнитное спиновое квантовое число, которое характеризует спин электрона.
Спин – собственный неуничтожимый механический момент импульса, не связанный с движением электрона в пространстве. Спин является квантовой величиной, это внутреннее, неотъемлемое свойство электрона, подобное его заряду и массе.
Спин квантуется по закону:
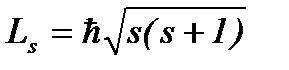, (8.9)
где s – спиновое квантовое число.
По аналогии с орбитальным моментом импульса, проекция спина Lsz квантуется так, что вектор Ls может принимать 2 s +1 ориентаций:
Lsz = ħ ms , (8.10)
где ms – магнитное спиновое квантовое число. Для электрона оно может принимать только два значения: ms = ± 1/2.
Для электронов в многоэлектронных атомах точное решение уравнения Шредингера невозможно. Применение приближенных методов показывает, что и в этом случае спектр энергии и других характеристик электрона является дискретным. Расселение электронов атома по разрешенным значениям энергии диктуется двумя основными принципами: стремлением каждого электрона занять состояние с наименьшей энергией и так называемым принципом запрета Паули, согласно которому в атоме не может быть двух электронов с одинаковым набором всех четырех квантовых чисел n , l , m и ms. Энергия электрона в многоэлектронном атоме зависит от двух первых квантовых чисел n и l, а при данном l возможны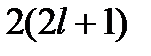 
разрешенных состояний, отличающихся проекциями орбитальных и спиновых моментов на направление внешнего поля. Поэтому на уровне 1s (n =1, l =0) могут находиться до 2-х электронов, на уровне 2s (n =2, l =0) – тоже 2 электрона, на уровне 2р (n =2, l =1) – до 6 электронов и т.д. В такой последовательности и застраиваются энергетические уровни (электронные оболочки) многоэлектронных атомов, входящих в Периодическую систему элементов. В результате в каждом атоме имеется одна или несколько заполненных электронами оболочек и одна, последняя, - незаполненная (она называется валентной оболочкой и от ее строения зависят химические свойства элемента). Выше валентного уровня энергии в спектре атома имеется еще очень много так называемых возбужденных уровней, на которые электроны атома могут переходить под влиянием внешних воздействий.
Примеры решения задач
Задача 1. Электрон в атоме находится в f-состоянии. Определите: 1) момент импульса электрона; 2) максимальное значение проекции момента импульса на направление внешнего магнитного поля.
| Дано: f -состояние |
| 1) Ll -? 2) ( Llz ) max -? |
Решение.
Состояние электрона характеризуется орбитальным квантовым числом l =3, а момент импульса (механический орбитальный момент) электрона равен:
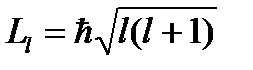(1)
где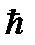 
— постоянная Планка.
Проекция момента импульса на направление внешнего магнитного поля
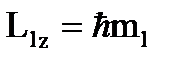, (2)
где ml = 0, ± 1, ± 2, ± 3, ….. ± l - магнитное квантовое число. Выражение (2) максимально при ml = ( ml ) max:
( Llz ) max = 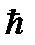( ml ) max (3)
где, по условию задачи, ( ml ) max = 3.
Подставив числовые значения, получаем:
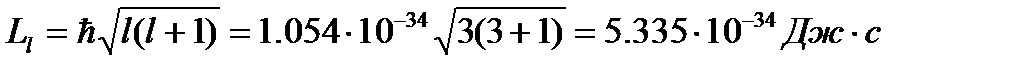
( Llz ) max = 1.054 × 10-34 × 3 = 3.162 × 10-34 Дж × с
Ответ: Ll = 5.335 × 10-34 Дж × с; ( Llz ) max = 3.162 × 10-34 Дж × с.
Задача 2. Сколько различных состояний может иметь электрон с главным квантовым числом n = 4?
| Дано: n = 4 |
| N - ? |
Решение.
При n=4 орбитальное квантовое число l может принимать значения 0, 1, 2, 3.
При l = 0 магнитное квантовое число ml может принимать только одно значение: ml = 0. Спиновое квантовое число ms может иметь два значения: ms = ½, -½. Cледовательно, в этом случае электрон может находиться в двух состояниях.
При l = 1 магнитное квантовое число ml может принимать значения: ml = 0, 1, -1, а магнитное квантовое число: ms = ½, -½. Поэтому общее число состояний электрона равно 6.
При l = 2 магнитное квантовое число ml может принимать значения: ml = 0, 1, -1, 2, -2, магнитное квантовое число: ms = ½, -½. Поэтому общее число состояний электрона на этом подуровне равно 10.
При l = 3 магнитное квантовое число ml может принимать значения: ml = 0, 1, -1, 2, -2, 3, -3, магнитное квантовое число: ms = ½, -½. Поэтому общее число состояний электрона на этом подуровне равно 14.
Общее число состояний, которые может иметь электрон с главным квантовым числом n = 4 равно: N = 2+6+10+14 = 32
Ответ: N = 32
Задача 3. Электрон в возбужденном атоме водорода находится в 3-d состоянии. Определите изменение орбитального магнитного момента электрона при переходе атома в основное состояние.
| Дано: l1 = 2 l2 = 0 |
| D pm - ? |
Решение.
Изменение орбитального магнитного момента равно:
D pm = pm 2 – pm 1 ,
где pm 1 и pm 2 – орбитальные магнитные моменты электрона в начальном (возбужденном) и конечном (основном) состояниях.
Модуль магнитного момента, обусловленного орбитальным движением электрона, равен:
,
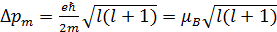где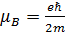 
–магнетон Бора, l – орбитальное квантовое число.
Учитывая значения l 1 и l 2 в возбужденном и основном состояниях, получаем:
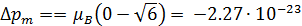Дж/Тл.
Знак «минус» показывает, что орбитальный магнитный момент уменьшается.
Ответ: Dpm = -2.27×10-23 Дж/Тл.
Задача 4. Пользуясь Периодической системой элементов, запишите электронную конфигурацию (распределение электронов по состояниям) атома брома, находящегося в основном состоянии.
Решение.
Согласно Периодической системе элементов, бром имеет порядковый номер 35, следовательно, электронная оболочка атома брома содержит 35 электронов.
Распределение электронов в атоме подчиняется принципу запрета Паули, в соответствии с которым два электрона, находящиеся в одном и том же атоме, не могут иметь одинаковый набор квантовых чисел.
Электронная конфигурация для атома брома запишется следующим образом:
1s22s22p63s23p63d104s24p5.
В данной записи цифры 1, 2, 3, 4 - главные квантовые числа, определяющие символ оболочки (соответственно K, L, M, N). Максимально возможное число электронов в K-оболочке 2, в L-оболочке – 8, в M-оболочке – 18, в N-оболочке – 32.
Обозначения 1s, 2s, 2p, 3s, 3p, 3d,... определяют символ подоболочки, при этом в s-состоянии может находиться 2 электрона, в р-состоянии – 6 электронов, в d-состоянии – 10 электронов.
К-оболочка (n =1, l = 0, ml = 0, ms = ± 1/2 )заполнена полностью и записывается, как 1s2 (то есть, на этой оболочке находятся два s - электрона).
Также полностью заполнены L- оболочка (2s22p6 – два 2s- электрона и шесть 2p-электронов) и M-оболочка (3s23p63d10 - два 3s-электрона, шесть 3p-электронов и десять 3d-электронов).
Оставшиеся семь электронов образуют незаполненную N – оболочку (4s24p5 – два 4s-электрона и пять 4р-электронов).
Ответ: 1s22s22p63s23p63d104s24p5.
Задачи для самостоятельного решения
1. Электрон в атоме находится в f-состоянии. Найти орбитальный момент импульса L ℓ электрона и максимальное значение проекции момента импульса (Ll , z)max на направление внешнего магнитного поля.
2. Момент импульса L ℓ орбитального движения электрона в атоме водорода равен 1,83∙10-34 Дж∙с. Определить магнитный момент Мℓ электрона, находящегося в 2р-состоянии в атоме водорода.
3. Используя принцип Паули, указать, какое максимальное число Nmax электронов в атоме могут иметь одинаковые следующие квантовые числа: 1) n, ℓ, m ℓ, ms; 2) n, ℓ, m ℓ; 3) n, ℓ; 4) n.
4. Найти число N электронов в атомах, у которых в основном состоянии заполнены: 1) K- и L-слои, 3s-оболочка и наполовину 3р-оболочка; 2) K-, L- и М- слои и 4s-, 4р- и 4d-оболочки. Что это за атомы?
5. Вычислить момент импульса L ℓ орбитального движения электрона, находящегося в атоме: 1) в s-состоянии; 2) в р-состоянии.
6. Определить возможные значения проекции момента импульса L ℓ z орбитального движения электрона в атоме на направление внешнего магнитного поля. Электрон находится в d –состоянии.
7. В атоме K, L и M оболочки заполнены полностью. Определите общее число электронов в атоме.
8. Найти число N электронов в атомах, у которых в основном состоянии заполнены: 1) K- и L-слои, 3s-оболочка и наполовину 3р-оболочка; 2) K-, L- и М- слои и 4s-, 4р- и 4d-оболочки. Что это за атомы?
9. Заполненной электронной оболочке соответствует главное квантовое число n= 4. Определите число электронов на этой оболочке, которые имеют одинаковое магнитное квантовое число ml = 0.
10. Определить возможные значения проекции момента импульса L ℓ z орбитального движения электрона в атоме на направление внешнего магнитного поля. Электрон находится в d –состоянии
Практические занятия 10-12
Дата: 2018-12-28, просмотров: 708.
