Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Внешний фотоэффект. Эффект Комптона»
2. Привитие навыков решения задач по данной теме.
Краткая теория
Фотоэлектрический эффект (фотоэффект) - явление взаимодействия электромагнитного излучения с веществом, в результате которого энергия излучения передаётся электронам вещества. Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом, если не сопровождается – внутренним. С елективный фотоэффект ‑ явление, которое наблюдается у ряда металлов, особенно щелочных, и проявляющееся в том, что кривая зависимости  имеет максимум на частоте собственных колебаний электронов металла (плазмонов). Величина фототока чувствительна к поляризации падающего свет.
имеет максимум на частоте собственных колебаний электронов металла (плазмонов). Величина фототока чувствительна к поляризации падающего свет.
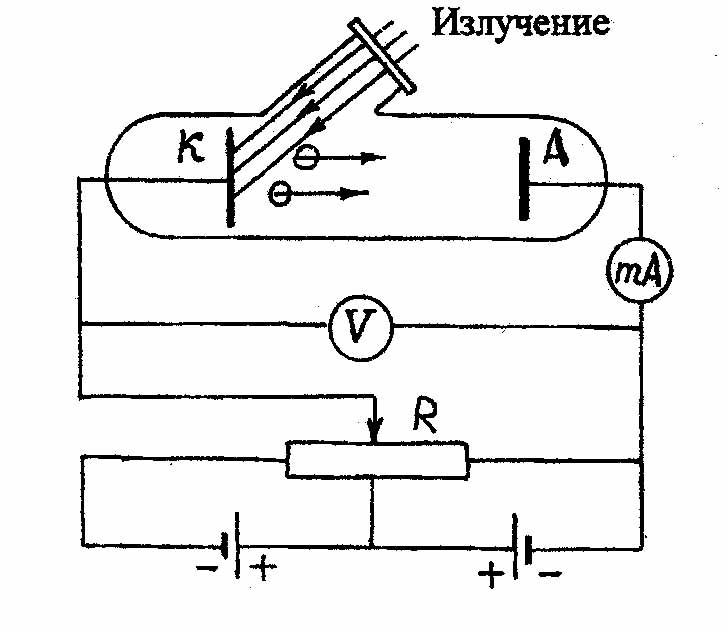
Впервые подробно фотоэффект был исследован русским ученым Столетовым. Схема его экспериментальной установки представлена на рис.3.1.
| 
|
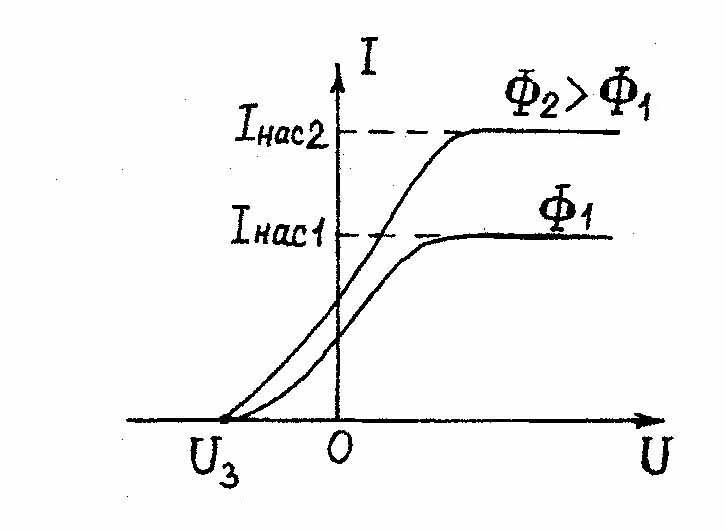
| Рис.3.1. Схема установки для изучения фотоэффекта | Рис.3.2. Вольтамперная характеристика внешнего фотоэффекта. |
Варьируя интенсивность и частоту излучения, а также материал катода, Столетов исследовал зависимость анодного тока от напряжения между катодом и анодом. Типичная вольтамперная кривая показана на рис.3.2.
При изучении вольт - амперных характеристик разнообразных материалов при различных частотах падающего на катод излучения и различных энергетических освещенностях катода в результате обобщения полученных данных были установлены следующие три закона внешнего фотоэффекта (законы Столетова для внешнего фотоэффекта):
1. Сила тока насыщения 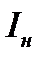 не зависит от длины волны падающего света, а определяется только интенсивностью освещения катода.
не зависит от длины волны падающего света, а определяется только интенсивностью освещения катода.
2. Максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
3. Для каждого вещества существует граничная частота νmin такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения.
Эти законы невозможно объяснить с точки зрения волновой теории света.
А. Эйнштейн в 1905 г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе предложенной им квантовой теории фотоэффекта. Согласно Эйнштейну, свет частотой v не только испускается, как это предполагал Планк, но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых Е = hv. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью с распространения света в вакууме. Кванты электромагнитного излучения получили название фотонов.
По Эйнштейну, каждый квант поглощается только одним электроном.
Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности света (I закон фотоэффекта). Энергия падающего фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии. По закону сохранения энергии:
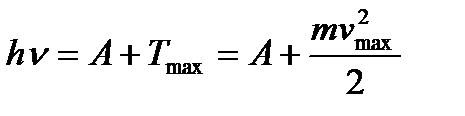 , (3.1)
, (3.1)
где h n - энергия фотона, падающего на поверхность металла; А - работа выхода электрона с поверхности металла; Т max - максимальная кинетическая энергия фотоэлектрона. Для практических целей это уравнения часто записывают в виде
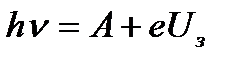 , (3.2)
, (3.2)
где 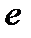 - заряд электрона,
- заряд электрона, 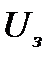 - задерживающее напряжение – напряжение, при котором фототок становится равным нулю.
- задерживающее напряжение – напряжение, при котором фототок становится равным нулю.
Красная граница фотоэффекта наблюдается тогда, когда энергия фотона равна работе выхода, т.е.
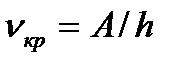 или
или 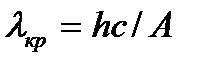 , (3.3)
, (3.3)
где nкр — минимальная частота света, при которой еще возможен фотоэффект; lкр — максимальная длина волны света, при которой еще возможен фотоэффект; h — постоянная Планка; с — скорость света в вакууме. Работа выхода 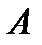 зависит от материала катода и чистоты его поверхности.
зависит от материала катода и чистоты его поверхности.
При высоких частотах используемого излучения на смену фотоэффекту приходит эффект Комптона: при падении на образец рентгеновского излучения с длиной волны 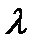 , после образца регистрируется излучение с двумя длинами волн
, после образца регистрируется излучение с двумя длинами волн 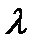 и
и 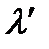 , причем
, причем 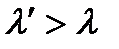 .
.
Экспериментально были установлено, что разность длин волн 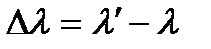 не зависит от материала образца, а определяется лишь углом наблюдения
не зависит от материала образца, а определяется лишь углом наблюдения 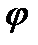 :
:
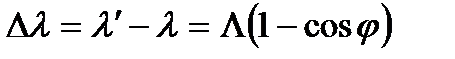 , (3.4)
, (3.4)
где 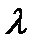 - длина волны фотона, встретившегося со свободным или слабосвязанным электроном;
- длина волны фотона, встретившегося со свободным или слабосвязанным электроном; 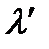 - длина волны фотона, рассеянного на угол j после столкновения с электроном;
- длина волны фотона, рассеянного на угол j после столкновения с электроном; 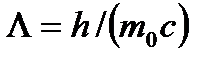 - комптоновская длина волны. Для электрона масса покоя
- комптоновская длина волны. Для электрона масса покоя 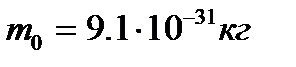 и L=2,436 пм.
и L=2,436 пм.
При увеличении угла 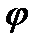 интенсивность излучения с длиной волны
интенсивность излучения с длиной волны 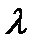 убывает, а с длиной волны
убывает, а с длиной волны 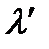 - возрастает. Аналогичная картина наблюдается и при уменьшении порядкового номера исследуемого элемента.
- возрастает. Аналогичная картина наблюдается и при уменьшении порядкового номера исследуемого элемента.
Правильное объяснение эффект Комптона получил лишь в квантовой физике. Здесь считается, что взаимодействие фотона рентгеновского излучения с электроном имеет характер упругого удара и поэтому выполняются законы сохранения импульса и энергии.
Комптоновская длина волны является естественным ограничением в точности определения координаты частицы с помощью электромагнитного излучения.
Излучение черного тела, фотоэффект, эффект Комптона служат доказательством квантовых (корпускулярных) представлений о свете, как о потоке фотонов. С другой стороны, такие явления, как интерференция, дифракция и поляризация света подтверждают волновую (электромагнитную) природу света. Наконец, давление и преломление света объясняются как волновой, так и квантовой теориями. Таким образом, электромагнитное излучение обнаруживает единство, непрерывных (волны) и дискретных (фотоны) свойств, которые взаимно дополняют друг друга.
Примеры решения задач.
Задача 1. Какая доля энергии фотона израсходована на работу вырывания фотоэлектрона, если красная граница фотоэффекта l0 = 307 нм, а максимальная кинетическая энергия 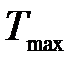 фотоэлектрона равна 1 эВ?
фотоэлектрона равна 1 эВ?
Дано:
l0 = 307 нм
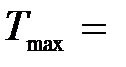 1 эВ
h = 6,63·10-34 Дж·с
с = 3·108 м/с 1 эВ
h = 6,63·10-34 Дж·с
с = 3·108 м/с
| СИ: 307·10-9 м 1,6·10-19 Дж |
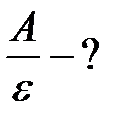
|
Решение:
Уравнение Эйнштейна для фотоэффекта – энергия кванта света e расходуется на работу выхода А электрона из вещества и на сообщение кинетической энергии Tmax (скорости) электрону:
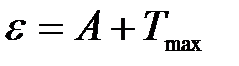 .
.
Работа выхода : 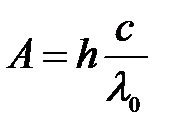 ,
,
где h – постоянная Планка; с – скорость света в вакууме.
Тогда отношение работы выхода к энергии фотона:
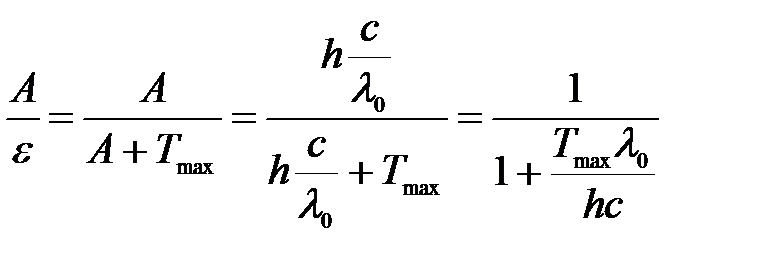 .
.
Вычислим:
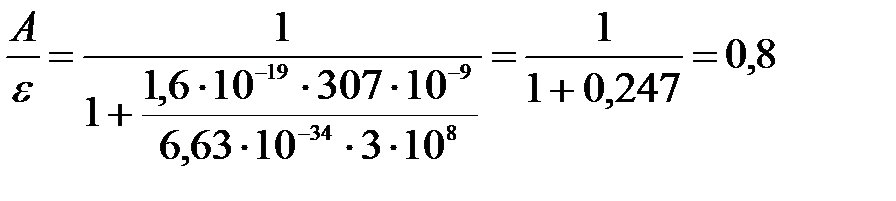 .
.
Ответ: 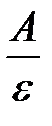 = 0,8.
= 0,8.
Задача 2. Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым светом платиновой пластинки, нужно приложить задерживающую разность потенциалов 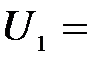 3,7 В; если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придётся увеличить до 6 В. Определить работу А выхода электронов с поверхности этой пластинки.
3,7 В; если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придётся увеличить до 6 В. Определить работу А выхода электронов с поверхности этой пластинки.
| Дано: U1 = 3,7 В U2 = 6 В А1 = 6,3 эВ | СИ: 10,08×10-19 Дж |
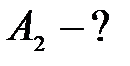
|
Решение:
Согласно уравнению Эйнштейна, при фотоэффекте энергия кванта света (e=h·v) расходуется на работу выхода электрона из вещества А и на сообщение кинетической энергии Т электрону:
e = А + Т.
Кинетическая энергия Т «гасится» работой сил электрического поля Аэл:
Т = Аэл. Учтём, что Аэл = еU. Тогда: 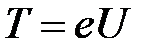 .
.
Тогда для первой и второй пластинки:
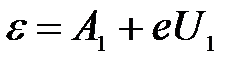 , ,
| |
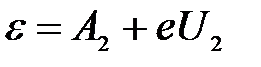 . .
|
Приравняем правые части уравнений:
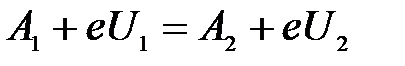 .
.
Выразим интересующую нас работу выхода для второй пластинки:
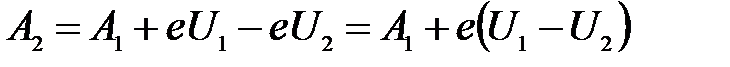 .
.
Подставим числа:
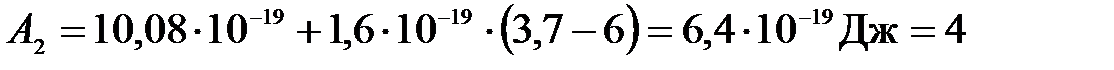 (эВ),
(эВ),
или сразу в электрон-вольтах:
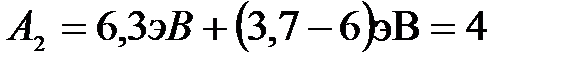 .
.
Ответ: А2 = 4 эВ.
Задача 3. “Красная граница” фотоэффекта для некоторого металла равна 500 нм. Определить: 1) работу выхода электронов из этого металла; 2) максимальную скорость электронов, вырываемых из этого металла светом, с длиной волны 400 нм.
| Дано: λ0 = 500 нм λ = 400 нм h = 6,63·10-34 Дж·с m = 9,11·10-31 кг с = 3·108 м/с | СИ: 5×10-7 м 4×10-7 м |
| 1) Авых = ? 2) υmax = ? |
Решение:
1) Уравнение Эйнштейна для «красной границы» при фотоэффекте:
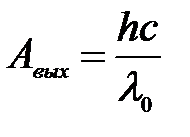 ,
,
где с – скорость света в вакууме, h – постоянная Планка.
Подставим числа:
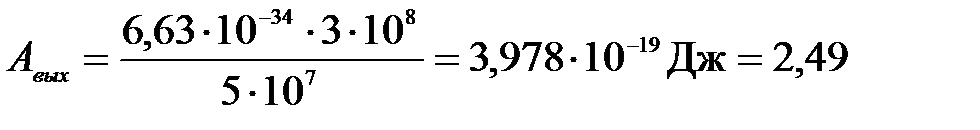 (эВ)
(эВ)
Следует напомнить, что 1 эВ = 1,6·10-19 Дж.
2) Согласно уравнению Эйнштейна, при фотоэффекте энергия кванта света ε расходуется на работу выхода электрона Авых из металла и на сообщение кинетической энергии Т электрону:
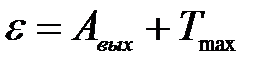 .
.
Энергия фотона: 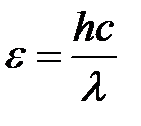 .
.
Кинетическая энергия: 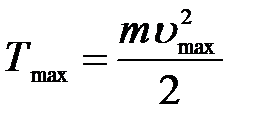 .
.
С учетом всех формул:
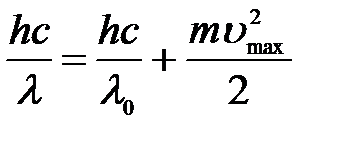 =>
=> 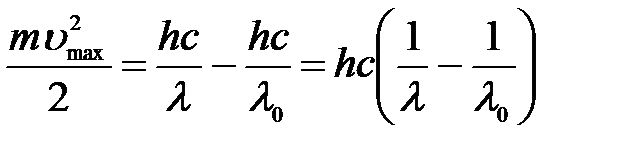 .
.
Откуда максимальная скорость электронов:
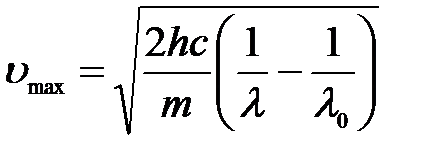 ,
,
где m – это масса электрона.
Подставим числа:
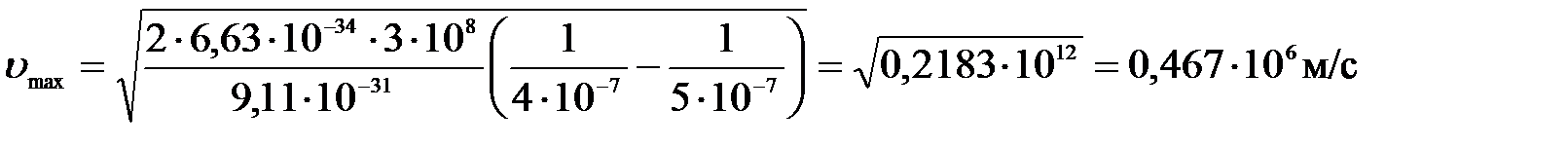 .
.
Ответ: 1) Авых = 2,49 эВ; 2) υmax = 467 км/с.
Задача 4. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпел рассеяние на угол 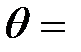 180°? Энергия (
180°? Энергия ( 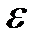 ) фотона до рассеяния равна 0,255 МэВ.
) фотона до рассеяния равна 0,255 МэВ.
Дано:
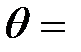 180° 180°
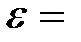 0,255 МэВ
Е0 = 0,511 МэВ 0,255 МэВ
Е0 = 0,511 МэВ
|
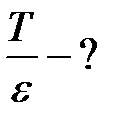
|
Решение:
Закон сохранения энергии:
e = 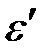 + Т,
+ Т,
где e – энергия падающего фотона, ε/ – энергия рассеянного (отразившегося) фотона, Т – кинетическая энергия электрона.
Выразим кинетическую энергию электрона отдачи Т:
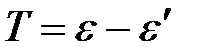 .
.
Тогда отношение кинетической энергии электрона отдачи к энергии падающего фотона:
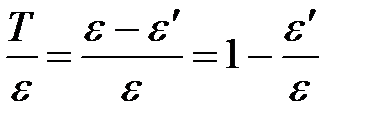 . .
|
Энергия рассеянного фотона: 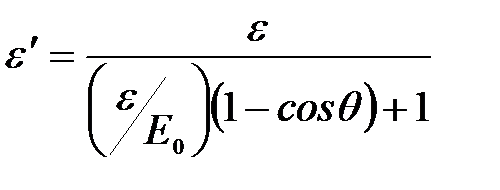 .
.
Откуда: 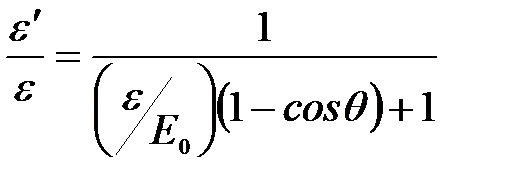 .
.
Следовательно, 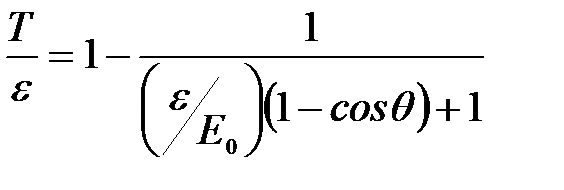 .
.
Произведём вычисления: 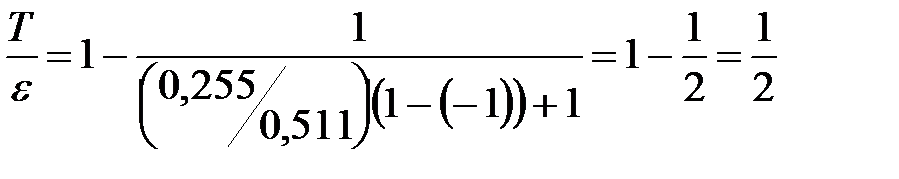 .
.
Ответ: 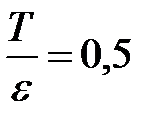 .
.
Задачи для самостоятельного решения
1. При освещении катода вакуумного фотоэлемента монохроматическим светом с длиной волны 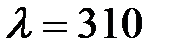 нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25%, задерживающее напряжение оказывается меньше на 0,8В. Определить по этим экспериментальным данным постоянную Планка.
нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25%, задерживающее напряжение оказывается меньше на 0,8В. Определить по этим экспериментальным данным постоянную Планка.
2. Плоский серебряный электрод освещается монохроматическим излучением с длиной волны 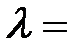 83 нм. Определить, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряжённостью Е = 10 В/см? «Красная граница» фотоэффекта для серебра
83 нм. Определить, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряжённостью Е = 10 В/см? «Красная граница» фотоэффекта для серебра 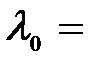 264 нм.
264 нм.
3. При освещении вакуумного фотоэлемента монохроматическим светом с длиной волны 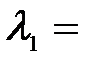 0,4 мкм он заряжается до разности потенциалов φ1 = 2 В. Определить, до какой разности потенциалов зарядится фотоэлемент при освещении его монохроматическим светом с длиной волны
0,4 мкм он заряжается до разности потенциалов φ1 = 2 В. Определить, до какой разности потенциалов зарядится фотоэлемент при освещении его монохроматическим светом с длиной волны 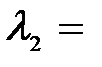 0,3 мкм?
0,3 мкм?
4. Выбиваемые светом при фотоэффекте электроны при облучении фотокатода видимым светом полностью задерживаются обратным напряжением 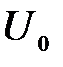 = 1,2 В. Специальные измерения показали, что длина волны падающего света
= 1,2 В. Специальные измерения показали, что длина волны падающего света 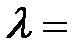 400 нм. Определить «красную границу» фотоэффекта.
400 нм. Определить «красную границу» фотоэффекта.
5. На цинковую пластину падает монохроматический свет с длиной волны 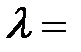 220 нм. Определить максимальную скорость
220 нм. Определить максимальную скорость 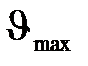 фотоэлектронов.
фотоэлектронов.
6. Определить длину волны l ультрафиолетового излучения, падающего на поверхность некоторого металла, при максимальной скорости фотоэлектронов равной 10 Мм/с. Работой выхода электронов из металла пренебречь.
7. Фотон ( 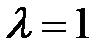 пм) рассеялся на свободном электроне под углом
пм) рассеялся на свободном электроне под углом 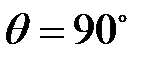 . Какую долю своей энергии фотон передал электрону?
. Какую долю своей энергии фотон передал электрону?
8. При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния 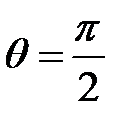 . Найти энергию (
. Найти энергию ( 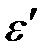 ) и импульс (
) и импульс ( 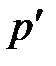 ) рассеянного фотона.
) рассеянного фотона.
9. Энергия 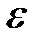 падающего фотона равна энергии покоя электрона. Определить долю
падающего фотона равна энергии покоя электрона. Определить долю 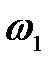 энергии падающего фотона, которую сохранит рассеянный фотон, и долю
энергии падающего фотона, которую сохранит рассеянный фотон, и долю 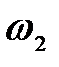 этой энергии, полученную электроном отдачи, если угол рассеяния
этой энергии, полученную электроном отдачи, если угол рассеяния 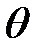 равен: 1) 60°; 2) 90°; 3) 180°.
равен: 1) 60°; 2) 90°; 3) 180°.
10. Определить, с какой скоростью должен двигаться электрон, чтобы его импульс ре был равен импульсу фотона рγ, длина волны которого l = 2 пм?
Практическое занятие 4
Тема: «Планетарная модель атома. Строение атома водорода по Бору. Спектры излучения атомов»
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Планетарная модель атома. Строение атома водорода по Бору. Спектры излучения атомов»
2. Привитие навыков решения задач по данной теме.
Краткая теория
В 19 веке впервые были открыты явления, обнаруживающие сложность строения и свойств атомов, которые до этого рассматривались как мельчайшие частицы вещества. Так в 1833 году М. Фарадей установил, что ток в растворе электролита – это упорядоченное движение заряженных частиц (ионов), минимальный заряд которых примерно равный е = 1,60∙10-19 Кл был назван элементарным электрическим зарядом. В 1896 году французский ученый Беккерель обнаружил явление естественной радиоактивности солей урана. Это явление исследовали Пьер и Мария Кюри, доказав, что из атомов вылетают и электроны, и положительно заряженные частицы (впоследствии названные α-частицами). На сложную структуру атомов указывали спектроскопические исследования, которые привели к открытию линейчатых спектров атомов. В начале XIX века были открыты дискретные спектральные линии в излучении атомов водорода в видимой части спектра, и впоследствии были установлены математические закономерности, связывающие длины волн этих линий (И. Бальмер, 1885 г.). В 1897 году Дж. Томсон открыл электрон и измерил отношение e/m заряда электрона к массе. Опыты Томсона подтвердили вывод о том, что электроны входят в состав атомов, причем носителями отрицательного заряда атомов являются легкие электроны, масса которых составляет лишь малую долю массы атомов. Основная часть массы атомов связана с положительным зарядом.
В первой модели атома Дж. Томсона (1903 г.) атом рассматривался как заполненный положительным электричеством шар, внутри которого находились электроны. Атом в целом был электронейтрален. Однако в дальнейшем выяснилась несостоятельность этой модели.
В начале ХХ века английский физик Э. Резерфорд, анализируя данные по рассеянию 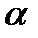 -частиц тонкими металлическими образцами, выдвинул так называемую «планетарную» модель строения атома.
-частиц тонкими металлическими образцами, выдвинул так называемую «планетарную» модель строения атома.
Рассеяние α-частиц при прохождении через фольгу вызывается кулоновскими силами, т.е. электрическим взаимодействием частицы и заряда атома. Гравитационное взаимодействие в 1033 раз меньше, поэтому фактически роли не играет.
Какие же заряды в атоме вызывают рассеяние α-частиц? Электроны не могут этого сделать, так как их масса много меньше массы частицы: ma=7350me. При взаимодействии с электронами быстро движущаяся частица не изменяет направление своего движения.
|
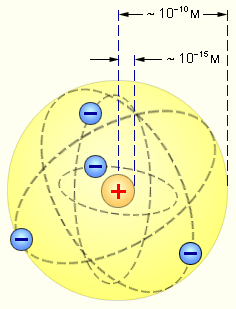
| Рис. 4.1. Планетарная модель атома |
Причиной рассеяния a-частиц является их взаимодействие с положительно заряженными частицами атома, занимающими очень малую область атома. Резерфорд назвал эту область ядром. В ядре сосредоточена почти вся масса атома и весь положительный заряд. Обобщив результаты опытов, Резерфорд предложил следующую модель строения атома, в рамках которой предполагается, что в центре атома находится тяжелое положительно заряженное ядро, вокруг которого, подобно планетам вокруг Солнца, вращаются легкие отрицательно заряженные электроны. Атомы имеют размеры порядка 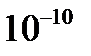 м, а ядра – порядка
м, а ядра – порядка 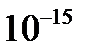 м, т.е. атом на 99.9% пустой (рис.4.1). Практически вся масса атома сосредоточена в ядре, поэтому ядерная материя обладает огромной плотностью:
м, т.е. атом на 99.9% пустой (рис.4.1). Практически вся масса атома сосредоточена в ядре, поэтому ядерная материя обладает огромной плотностью: 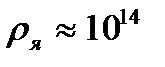 г/cм3.
г/cм3.
Однако планетарная модель атома является внутренне противоречивой. Движущийся с ускорением заряд излучает электромагнитную волну. При этом энергия атома уменьшается: электрон должен упасть на ядро, а атом прекратить свое существование.
На самом деле атомы химических элементов представляют собой устойчивые структуры, существующие десятки тысяч лет без изменения. Поэтому модель атома Резерфорда была дополнена рядом положений, автором которых является датский физик Бор.
В 1913 году Бор показал, что несовпадение с экспериментом выводов, основанных на модели Резерфорда, возникло потому, что поведение микрочастиц нельзя описывать теми же законами, что и макроскопических тел.
Бор предположил, что величины характеризующие микромир, должны квантоваться, т.е. они могут принимать только определенные дискретные значения.
Законы микромира - квантовые законы. Эти законы в начале 20 столетия еще не были установлены наукой. Бор сформулировал их в виде трех постулатов, дополняющих ( и "спасающих") атом Резерфорда.
Первый постулат (постулат стационарных состояний) :
Атомы имеют ряд стационарных состояний соответствующих определенным значениям энергий: Е1, Е2...En. Находясь в стационарном состоянии, атом энергии не излучает и не поглощает энергию, несмотря на движение электронов. Энергии стационарных состояний образуют дискретный спектр.
Второй постулат (правило квантования орбит):
В стационарном состоянии атома электроны движутся по стационарным орбитам, для которых выполняется квантовое соотношение:
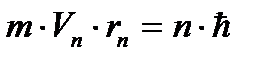 (4.1)
(4.1)
где m - масса электрона, rn- радиус орбиты с номером n (n=1,2,3...), 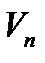 - скорость электрона на этой орбите, ħ - постоянная Планка.
- скорость электрона на этой орбите, ħ - постоянная Планка.
Третий постулат (правило частот):
Излучение или поглощение энергии атомом происходит при переходе его из одного стационарного состояния в другое. При этом излучается или поглощается порция энергии (квант), равная разности энергий стационарных состояний, между которыми происходит переход:
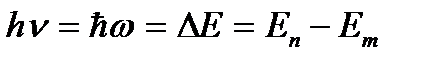 (4.2)
(4.2)
Постулаты Бора противоречат законам классической физики. Они выражают характерную особенность микромира - квантовый характер происходящих там явлений. Выводы, основанные на постулатах Бора, хорошо согласуются с экспериментом. Например, объясняют закономерности в спектре атома водорода, происхождение характеристических спектров рентгеновских лучей и т.д. На рис. 4.2 показана часть энергетической диаграммы стационарных состояний атома водорода.
Планетарная модель продемонстрировала прекрасное согласие с экспериментом при описании атома водорода, однако для описания свойств многоэлектронных атомов она оказалась не пригодна. Основной недостаток этой модели заключается в отсутствии учета взаимодействия электронов между собой.
Постулаты Бора нашли своё экспериментальное подтверждение в опытах Д.Франка и Г.Герца (1913), в которых изучались столкновения электронов с атомами газов.
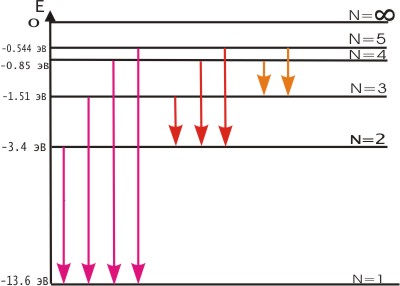
Рис. 4.2. Энергетическая диаграмма стационарных состояний атома водорода
Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем - систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не+, Li2+), а также теоретически вычислить постоянную Ридберга. 
Выражение для радиуса n-й стационарной орбиты:
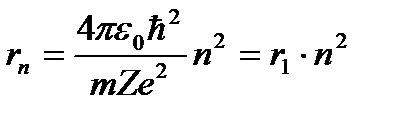 , ( n = 1, 2, 3, …). (4.3)
, ( n = 1, 2, 3, …). (4.3)
Для атома водорода (Z = 1) радиус первой орбиты электрона при n = 1, называемый первым боровским радиусом (rB), равен
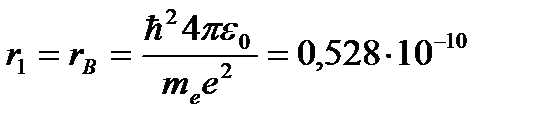 (4.4)
(4.4)
Полная энергия электрона в водородоподобной системе складывается из его кинетической энергии 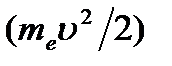 и потенциальной энергии в электростатическом поле ядра
и потенциальной энергии в электростатическом поле ядра 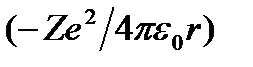 :
:
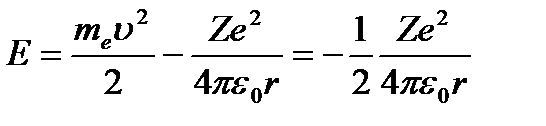 (4.5)
(4.5)
Учитывая квантованные для радиуса n-й стационарной орбиты значения (4.4), получим, что энергия электрона может принимать только следующие дозволенные дискретные значения:
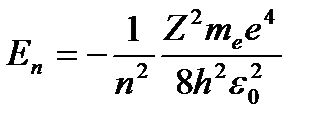 (n = 1, 2, 3, …), (4.6)
(n = 1, 2, 3, …), (4.6)
где m - масса электрона, e = 1.610-19 Кл - и заряд электрона; 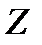 – порядковый номер элемента в таблице Менделеева. Знак « - » означает, что электрон находится в связанном состоянии.
– порядковый номер элемента в таблице Менделеева. Знак « - » означает, что электрон находится в связанном состоянии.
Из формулы (4.6) следует, что энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения n. Целое число n в выражении (3.6), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n = 1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.
Придавая n различные целочисленные значения, получим для атома водорода (Z = 1) возможные уровни энергии, схематически представленные на рис.4.2 и 4.3. На рис.4.2 изображена диаграмма энергетических уровней атома водорода и указаны переходы, соответствующие различным спектральным сериям. Рис.4.3 иллюстрирует образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.
Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n = ∞. Атом водорода обладает, таким образом, минимальной энергией (Е1=-13,6 эВ) при п = 1 и максимальной (Е∞ = 0) при n = ∞. Следовательно, значение Е∞ = 0 соответствует ионизации атома (отрыву от него электрона). Согласно третьму постулату Бора, при переходе атома водорода ( Z = 1) из стационарного состояния n в стационарное состояние т с меньшей энергией испускается квант
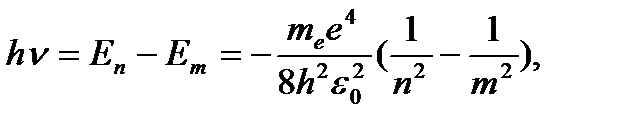 (4.7)
(4.7)
Откуда частота излучения
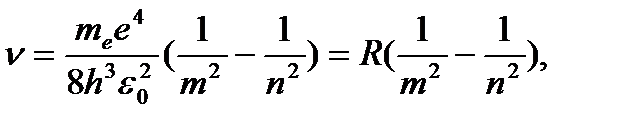 (4.8)
(4.8)
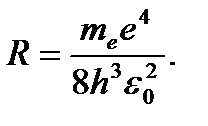 (4.9)
(4.9)
R – постоянная Ридберга.
Прекрасное согласие боровской теории атома водорода с экспериментом служило веским аргументом в пользу ее справедливости. Стало ясно, что атомы – это квантовые системы. Энергетические уровни стационарных состояний атомов дискретны.
Однако попытки применить теорию Бора к более сложным атомам (даже для атома гелия) не увенчались успехом. Эта теория обладает внутренними противоречиями: с одной стороны, применяет законы классической физики, а с другой - основывается на квантовых постулатах. Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано де Бройлем (1923) на основе представлений о волновых свойствах частиц.
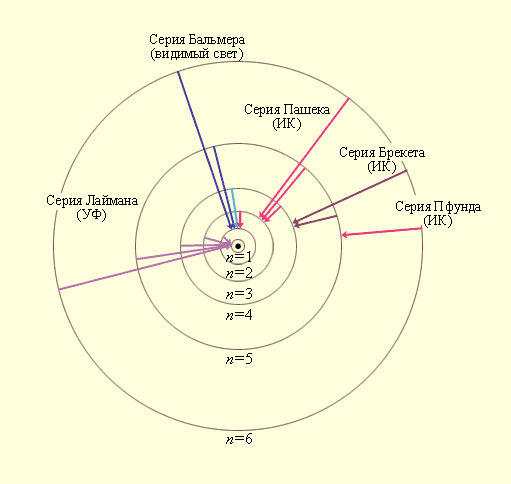
Рис.4.3. Стационарные орбиты атома водорода и образование
спектральных серий.
Примеры решения задач
Задача 1. Определить потенциальную П, кинетическую Т и полную Е энергии электрона, находящегося на первой орбите атома водорода (основное состояние).
| Дано: Z = 1 n = 1 mе = 9,11·10-31 кг е = 1,6·10-19 Кл h = 6,626·10-34 Дж·с ε0 = 8,85·10-12 Ф/м |
| 1) П = ? 2) Т = ? 3) Е = ? |
Решение:
Потенциальная энергия электрона в электростатическом поле ядра и радиус орбиты rn электрона:
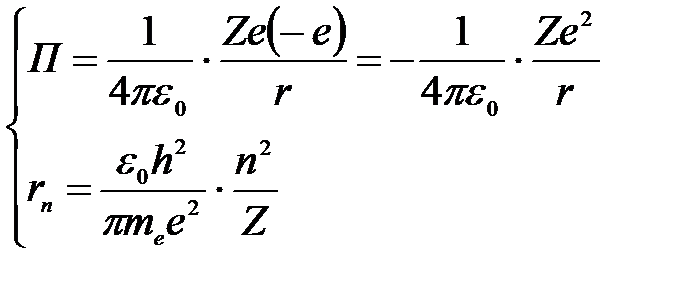 .
.
Тогда потенциальная энергия электрона на любой орбите водородоподобного атома (считаем энергию электрона в бесконечности равной нулю):
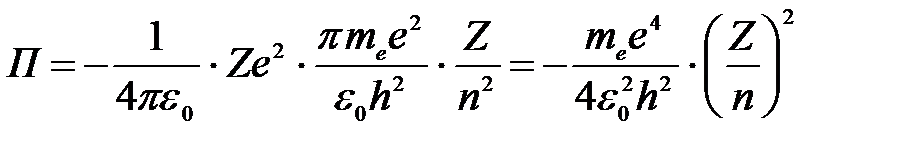 . .
|
Потенциальная энергия для основного состояния атома водорода Z = 1, n = 1:
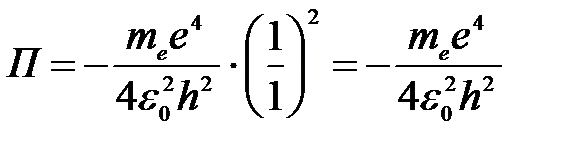 .
.
Вычислим:
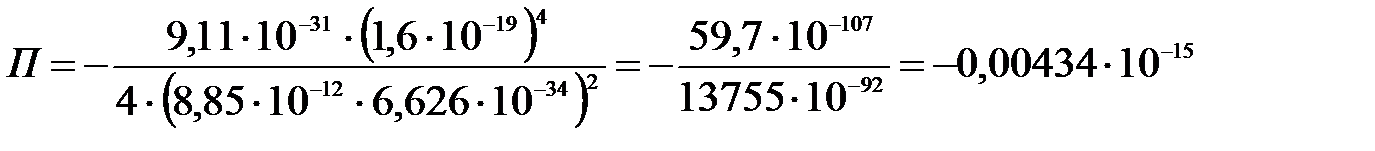 ;
;
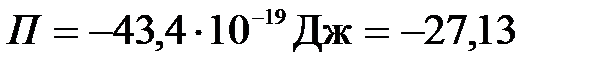 эВ.
эВ.
2) Кинетическая энергия электрона при движении по окружности и скорость электрона на этой орбите :
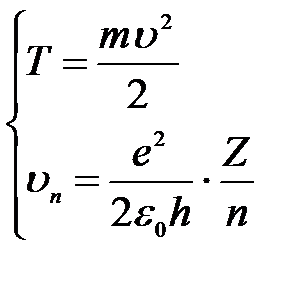 .
.
Тогда кинетическая энергия электрона на любой орбите водородоподобного атома:
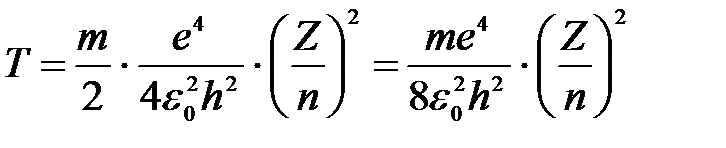 . .
|
Кинетическая энергия для основного состояния атома водорода Z=1, n=1:
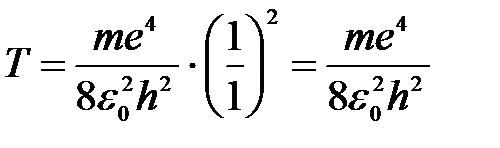 .
.
Вычислим:
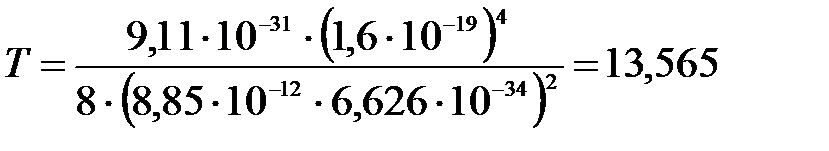 эВ.
эВ.
3) Полная энергия электрона на любой орбите водородоподобного атома:
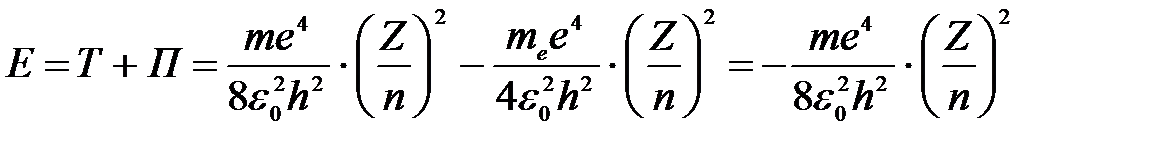 . .
| (3) |
Полная энергия для основного состояния атома водорода Z = 1, n = 1:
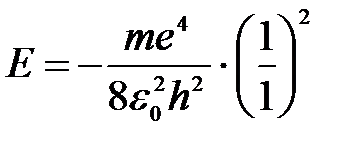 .
.
Вычислим:
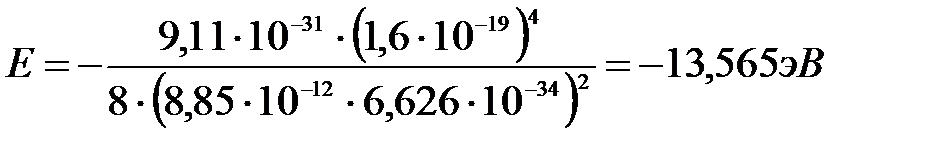 .
.
Задача 2. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.
| Дано: Z = 1 m = 2 n = 3 h=6,626·10-34 Дж·с с = 3·108 м/с R = 3,29 1015 c-1 R/ = 1,097 107 м-1 Е i = 13,6 эВ mе = 9,11·10-31 кг е = 1,6·10-19 Кл |
| ε3,2 =? |
Решение:
Способ 1. Энергия фотона:
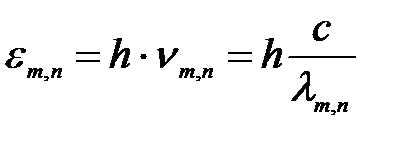 , (1)
, (1)
где h – постоянная Планка, с – скорость света в вакууме, ν – частота излучения, λ – длина волны излучения m, n – стационарные орбиты; m = 1, 2, 3, 4, 5, 6 (определяет серию), n = m + 1, m + 2, m + 3…(определяет отдельные линии этой серии), n = ∞ определяет границу серии.
Обобщённая формула Бальмера (сериальная формула):
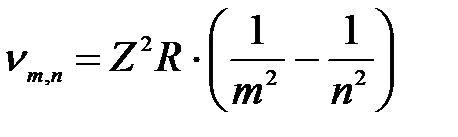 (2)
(2)
или 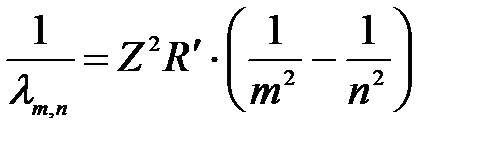 , (2-а) , (2-а)
|
где R = R/с = 3,28805∙1015 1/с – постоянная Ридберга,
R/ = 1,097373177∙107 м-1 – штриховая постоянная Ридберга,
Z – зарядовое число (порядковый номер в таблице Менделеева).
Подставим формулу (2) частоты в (1):
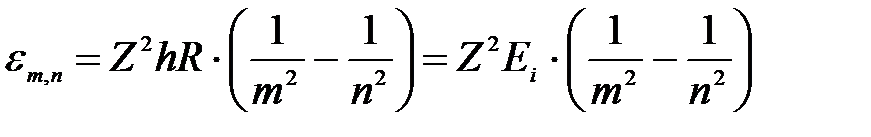 , ,
| (3а) |
или через длину волны:
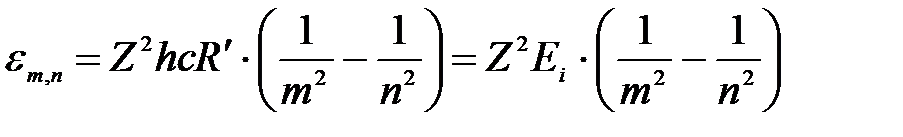 , ,
| (3б) |
где Е i – энергия ионизации водорода. Получили одинаковую формулу.
Произведем вычисления во внесистемных единицах:
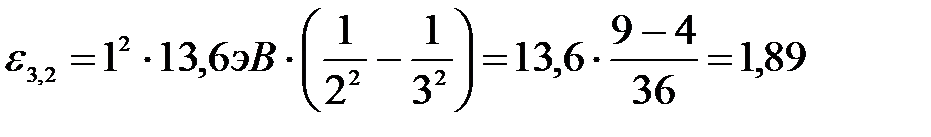 (эВ).
(эВ).
Способ 2. Второй постулат Бора (правило частот):
| εn,m = ΔЕ = Еn – Em = Eдо – Eпосле, | (4) |
где ε n,m – энергия испускаемого (поглощаемого) атомом фотона при переходе атома из одного стационарного состояния в другое; Еn и Em – энергии стационарных состояний, характеризуемые квантовыми числами n и m, определяемые по формуле:
 , ,
| (5) |
где е – элементарный заряд, ε0 – электрическая постоянная, Z – атомный номер (зарядовое число, порядковый номер атома в таблице Д.И. Менделеева).
При Em < En происходит излучение фотона, при Em > En – его поглощение.
Тогда энергия испускаемого фотона:
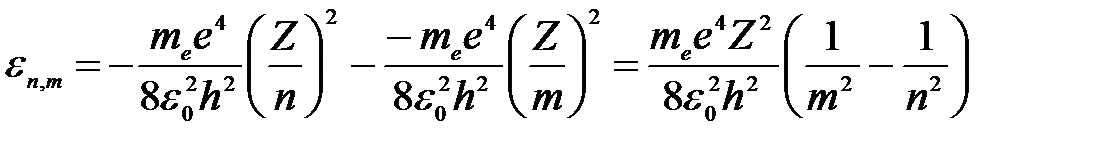 .
.
Подставим числа:
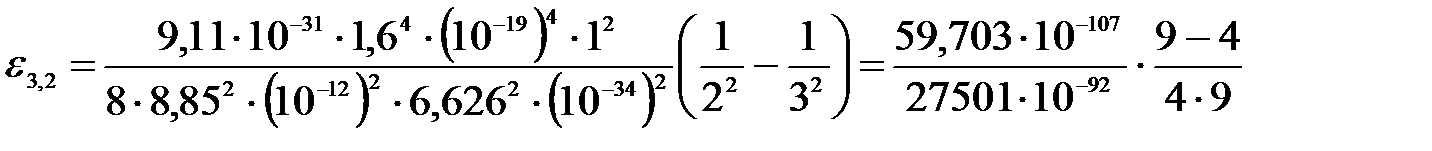 ;
;
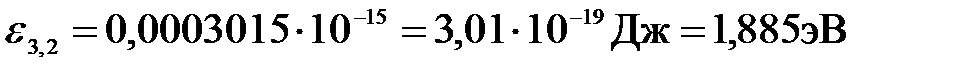 .
.
Ответ: ε3,2 = 1,89 эВ, относится к серии Бальмера.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| орбита |
| e |
| Рис. 4.4 |
Задача 3. Определить длину волны спектральной линии, соответствующую переходу электрона в атоме водорода с шестой боровской орбиты на вторую (рис.4.4) К какой серии относится эта линия? Которая она по счёту?
Дано:
m = 2
n = 6
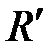 = 1,097 107 м-1 = 1,097 107 м-1
|
| l =? |
Решение:
Запишем обобщенную формулу Бальмера:
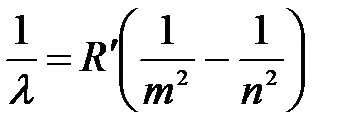 ,
,
где l – длина волны спектральных линий в спектре атома Бора; m – определяет серию; n – определяет отдельные линии этой серии (m < n); 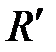 – штриховая постоянная Ридберга.
– штриховая постоянная Ридберга.
Отсюда длина волны:
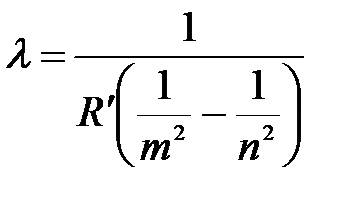 .
.
Произведем вычисления:
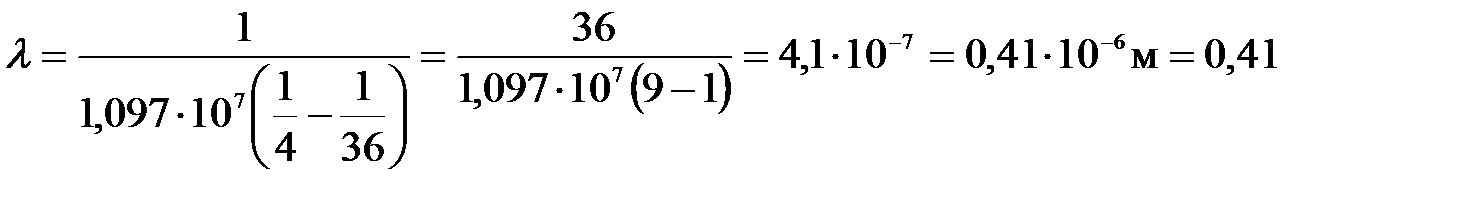 мкм.
мкм.
Это – серия Бальмера, т.к. m = 2. По счёту она 4я, т.к. n – m = 6 – 2 =4.
Ответ: l = 0,41 мкм, серия Бальмера, по счёту № 4.
Задача 4. Насколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны l = 486 нм?
| Дано: Z = 1 l = 486 нм | СИ: 486∙10-9 м |
| DЕк -? |
Решение:
Из закона сохранения энергии: разность полных энергий электрона соответствующих орбит равна энергии излучения:
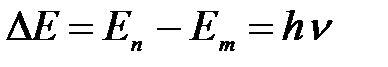 .
.
Частота это есть отношение скорости света к длине волны:
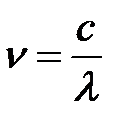 .
.
Полная энергия электрона по модулю равна кинетической энергии:
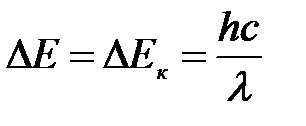 .
.
Подставим численные значения:
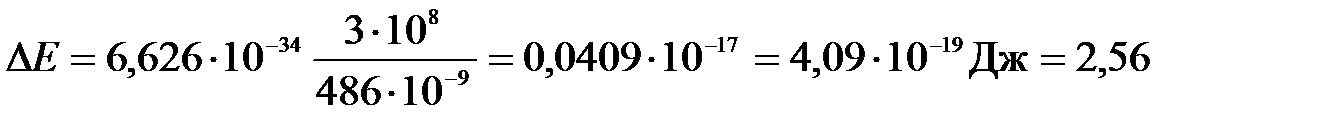 (эВ).
(эВ).
Ответ: DЕк = 2,56 эВ.
Задачи для самостоятельного решения
1. Рассмотрите стационарное состояние атома водорода с n = 50 в рамках боровской модели. Вычислите: а) энергию связи электрона в эВ; б) радиус орбиты электрона; в) частоту обращения электрона на орбите; г) длину волны излучения, испущенного при переходе между стационарными состояниями с n =50 и n = 49 .
2. Спутник с массой 10 кг обращается вокруг Земли за 2 часа по орбите радиусом 8000 км. а) Считая, что постулат Бора о моменте количества движения применим к спутнику в той же мере, как и к электрону атома водорода, определите квантовые числа орбиты спутника; б) покажите, исходя из первого постулата Бора и закона тяготения Ньютона, что радиус орбиты спутника прямо пропорционален квадрату квантового числа: r = kn2, где k – коэффициент пропорциональности; в) используя результат (б), определите расстояние между орбитой спутника, данной в условии задачи и следующей «разрешенной» орбитой; г) подумайте над возможностью наблюдения разделения двух соседних орбит; д) совпадают ли квантовая и классическая орбиты спутника? Какой из методов вычисления орбит «правильный»?
3. В каких пределах должна быть энергия бомбардирующих электронов, чтобы при возбуждении атома водорода ударами этих электронов спектр излучения водорода имел лишь одну спектральную линию? Энергия атома водорода в основном состоянии E1 = – 13,6 эВ.
4. Найдите скорость электронов, вырываемых электромагнитным излучением с длиной волны 18 нм из иона Не+, находящегося в основном состоянии. Энергия ионизации атома водорода 13,6 эВ.
5. Вычислить радиус второй орбиты r2 электрона в ионе гелия He+.
6. Вычислить скорость υ4 электрона на четвёртой орбите для иона лития Li++.
7. Найти энергию Е i и потенциал Ui ионизации иона He+.
8. Найти первую энергию возбуждения Е1 и первый потенциал возбуждения U1 иона Li++.
9. Определить длину волны l, соответствующую второй спектральной линии в серии Пашена.
10. Определить максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера).
Практическое занятие 5
Дата: 2018-12-28, просмотров: 1500.