Двойственная природа микрочастиц математически выражается в так называемых соотношениях неопределенностей, сформулированных в 1927 г. В. Гейзенбергом. Соотношения неопределенностей для координат и импульсов имеют вид:
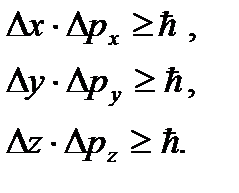(5.2)
для энергии и времени:
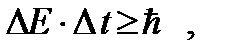(5.3)
Соотношение (5.3) логически вытекает из хорошо известной в теории колебаний связи, существующей между длительностью сигнала Dt и полосой частот Dw:
(5.4)
Поскольку для микрочастиц справедлива формула
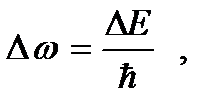(5.5)
то, очевидно, можно написать, что
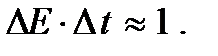(5.6)
Соотношения неопределенностей для координат и импульсов также вытекают из известной классической формулы, связывающей ширину волнового пакета Dx с разбросом волновых чисел Dkx:
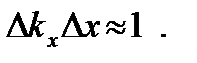(5.7)
Таким образом, если признать справедливыми приведенные выше классические закономерности, а также два фундаментальных постулата квантовой теории ( 
), то соотношения неопределенностей получаются из них, как прямое следствие.
Сущность соотношения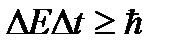 
может быть определена следующим образом: погрешность измерения энергии 
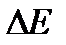определяется интервалом времени 
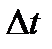, в течение которого может быть произведено данное измерение.
Сущность соотношений неопределенностей состоит в том, что невозможно одновременно точно определить координаты (x , y , z) и соответствующие проекции импульса (px , py , pz). Причем, это не связано с несовершенством методов измерения, а определяется двойственной корпускулярно-волновой природой микрообъектов.
Примеры решения задач
Задача 1. Электрон прошел ускоряющую разность потенциалов 51 В. Найти длину волны де Бройля для электрона.
| Дано: U = 51 В |
| l Б - ? |
Решение:
Запишем формулу де Бройля:
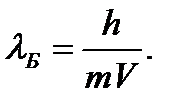
Пройдя ускоряющую разность потенциалов, электрон приобрел кинетическую энергию (нерелятивистский случай):
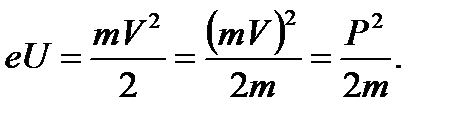
Отсюда выразим импульс электрона и запишем выражение для длины волны де Бройля:
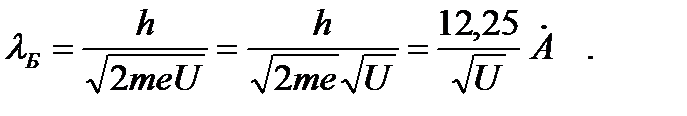
Вычислим длину волны де Бройля:
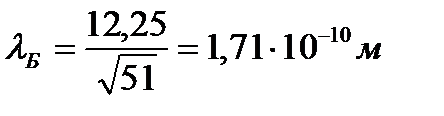
Ответ: λБ = 1,71 Å
Задача 2. Вычислите дебройлевские длины волн электрона, протона и атома урана, имеющих одинаковую кинетическую энергию 100 эВ.
| Дано: Wk = 100 эВ | СИ: 1.6 × 10-17 Дж |
| l Б - ? |
Решение
Кинетическая энергия нерелятивистских частиц определяется выражением
.
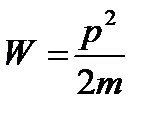Откуда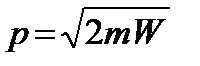 
.
Дебройлевская длина волны электрона
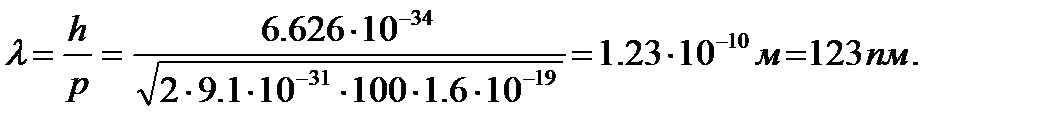
Дебройлевская длина волны протона
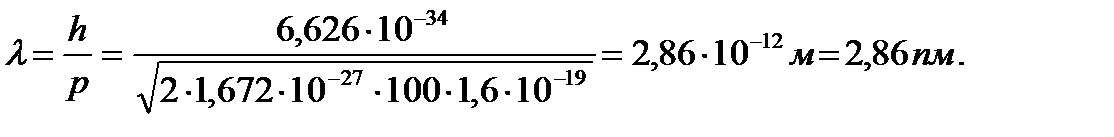
Дебройлевская длина волны атома урана:
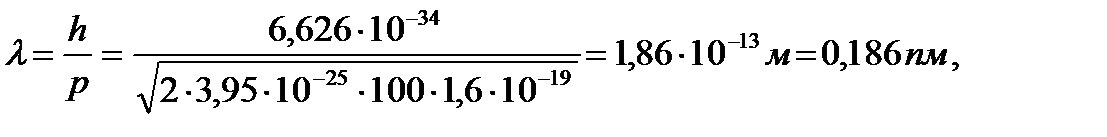
где масса атома урана
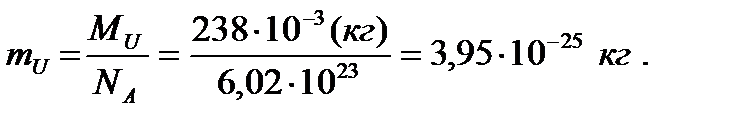
Задача 3. Кинетическая энергия электрона в атоме (К) составляет величину 10 эВ. Оценить минимальные размеры атома, используя соотношение неопределенностей.
| Дано: К = 10 эВ me = 9.11 × 10-31 кг | СИ: 1.6 × 10-18 Дж |
| lmin - ? |
Решение
Электрон находится в атоме, линейные размеры которого l. Следовательно, неопределенность координаты равна:
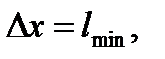
Запишем соотношение неопределенностей, подставив величину Δх:
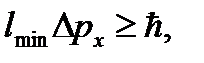
где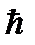 
= 1.054 × 10-34 Дж × с – постоянная Планка.
Поскольку надо найти минимальные размеры атома, то Dpx не должно превышать px, т.е. Dpx = px. Импульс связан с кинетической энергией электрона соотношением:
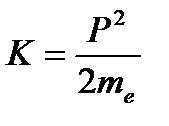
Из последнего уравнения выразим импульс электрона, подставим его в соотношение неопределенностей и решим полученное уравнение относительно минимально линейного размера атома:
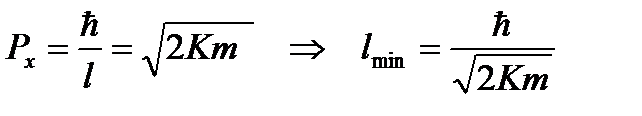
Подставив числовые значения, рассчитаем минимальный размер атома:
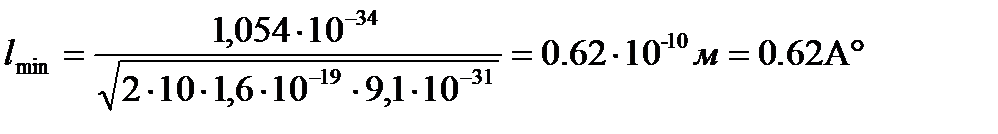
Ответ: lmin = 0.62 Å.
Задача 4. Атом излучает фотон с длиной волны 550 нм. Время излучения 10-8 с. Определить неточность в определении указанной длины волны и с какой точностью может быть определено местонахождение данного фотона в направлении его движения.
| Дано: l = 550 нм D t = 10-8 с c = 3 × 108 м/ c | СИ 5.5 × 10-7 м |
| D l - ? D x - ? |
Решение
Запишем уравнение для расчета энергии кванта (фотона):
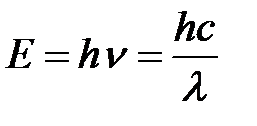
Для нахождения неточности в определении указанной длины волны (Δλ) возьмем производную от энергии по длине волны и выразим неточность в определении энергии кванта ΔЕ:
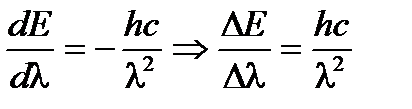
Запишем соотношение неопределенностей для энергии и выразим из него неточность в определении энергии излученного кванта (фотона) ΔЕ:
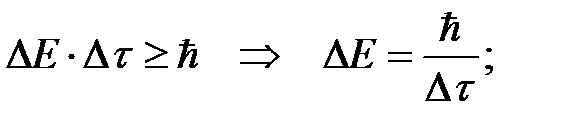
Приравняем выражения для величины ΔЕ, полученные выше. Решим последнее уравнение относительно искомой величины Δλ:
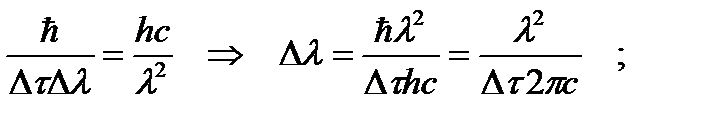
Запишем уравнение де Бройля относительно импульса фотона. Возьмем производную от импульса по λ и выразим неточность в определении его импульса ΔР:
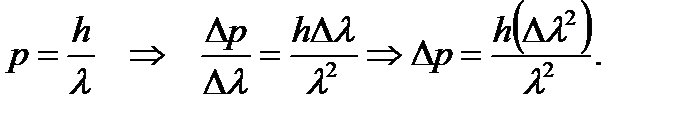
Используем соотношение неопределенностей для расчета величины неточности в определении координаты фотона ΔХ:
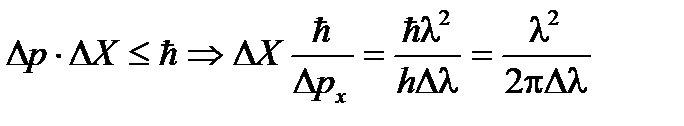
Произведем вычисления заданных величин:
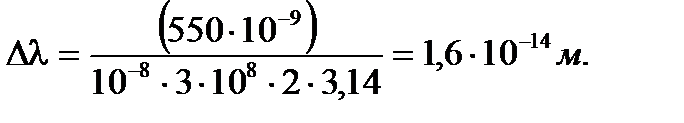
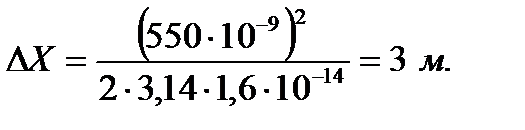
Ответ: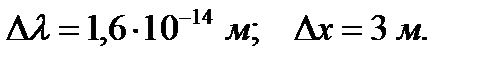 
Задачи для самостоятельного решения
1. Электрон движется по окружности радиусом R = 0,5 см в однородном магнитном поле с индукцией В = 8 мТл. Определить длину его волны де Бройля.
2. Определить длину волны де Бройля для нейтрона, движущегося со наиболее вероятной скоростью при комнатной температуре.
3. Найти длину волны де Бройля lБ для электрона, движущегося по круговой орбите атома водорода, находящегося в основном состоянии.
4. Найти длину волны де Бройля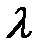 
для атома водорода, движущегося при температуре 
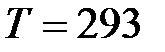К со: 1) средней квадратичной скоростью; 2) наиболее вероятной скоростью; 3) средней арифметической скоростью.
5. Найти длину волны де Бройля λ протона, прошедшего ускоряющую разность потенциалов U: 1) 1кВ; 2) 1ГВ.
6. Время жизни атома в возбужденном состоянии t=10 нс. Учитывая, что постоянная Планка ћ = 6,6×10-16 эВ×с, определите ширину энергетического уровня (в эB).
7. Среднее время жизни возбуждённого состояния атома равно τ = 12 нс. Определите минимальную неопределённость длины волны Δλ = 0,12 мкм излучения при переходе атома в основное состояние.
8. Оцените наименьшие ошибки, с которыми можно определить скорость шарика массой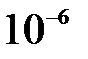 
кг и электрона, если положение центра шарика и положение электрона установлены с точностью 
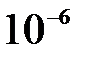м. Постоянная Планка 
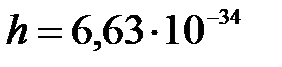Дж·с.
9. Определить неопределенность в определении координаты электрона, движущегося в атоме водорода со скоростью v=1,5 Мм/с, если допускаемая неопределенность скорости составляет 10% от её величины. Сравнить полученный результат с диаметром атома водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.
10. Используя соотношение неопределённостей энергии и времени, определить естественную ширину спектральной линии излучения атома при переходе его из возбуждённого состояния в основное. Среднее время жизни атома в возбуждённом состоянии принять равным 10нс, а длину волны излучения - равной 600 нм.
Практические занятия 6-7
Дата: 2018-12-28, просмотров: 689.
