Цель:

1. Закрепление теоретических знаний дисциплины по теме: «Элементы квантовой статистики. Зонная структура твердых тел. Электропроводность полупроводников. Контактные явления».

2. Привитие навыков решения задач по данной теме.

Краткая теория

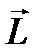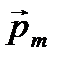Применение квантовомеханического подхода к анализу поведения электрона в атоме водорода показало, что не только его энергия, но и связанный с движением вокруг ядра его момент импульса L, обусловленный этим же движением магнитный момент p_m, а также проекции векторов   и  на направление внешнего магнитного поля могут принимать лишь вполне определенные дискретные значения, т.е. квантуются. Разрешенные значения этих величин определяются целочисленными параметрами n , l и m, называемыми квантовыми числами. Позднее к ним было добавлено еще одно квантовое число m_s, которое определяет разрешенные значения проекции на направление внешнего магнитного поля так называемых спиновых момента импульса и магнитного момента, не связанных с движением электрона вокруг ядра, а присущих большинству элементарных частиц по самой их природе.

Для электронов в многоэлектронных атомах точное решение уравнения Шредингера невозможно. Применение приближенных методов показывает, что и в этом случае спектр энергии и других характеристик электрона является дискретным. Расселение электронов атома по разрешенным значениям энергии диктуется двумя основными принципами: стремлением каждого электрона занять состояние с наименьшей энергией и так называемым принципом запрета Паули, согласно которому в атоме не может быть двух электронов с одинаковым набором всех четырех квантовых чисел n , l , m и m_s. Энергия электрона в многоэлектронном атоме зависит от двух первых квантовых чисел n и l, а при данном l возможны 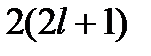разрешенных состояний, отличающихся проекциями орбитальных и спиновых моментов на направление внешнего поля. Поэтому на уровне 1s (n =1, l =0) могут находиться до 2-х электронов, на уровне 2s (n =2, l =0) – тоже 2 электрона, на уровне 2р (n =2, l =1) – до 6 электронов и т.д. В такой последовательности и застраиваются энергетические уровни (электронные оболочки) многоэлектронных атомов, входящих в Периодическую систему элементов. В результате в каждом атоме имеется одна или несколько заполненных электронами оболочек и одна, последняя, - незаполненная (она называется валентной оболочкой и от ее строения зависят химические свойства элемента). Выше валентного уровня энергии в спектре атома имеется еще очень много так называемых возбужденных уровней, на которые электроны атома могут переходить под влиянием внешних воздействий. Схема расселения электронов по энергетическим уровням в атоме представлена на рис.10.1.

Если перейти от рассмотрения движения одной микрочастицы (одного электрона) к многоэлектронным системам, то проявляются особые свойства, не имеющие аналогов в классической физике. Пусть квантово-механическая система состоит из одинаковых частиц, например электронов. Все электроны имеют одинаковые физические свойства – массу, электрический заряд, спин и другие внутренние характеристики (например квантовые числа). Такие частицы называют тождественными.

Необходимые свойства системы одинаковых тождественных частиц проявляются в фундаментальном принципе квантовой механики – принципе неразличимости тождественных частиц, согласно которому невозможно экспериментально различить тождественные частицы.

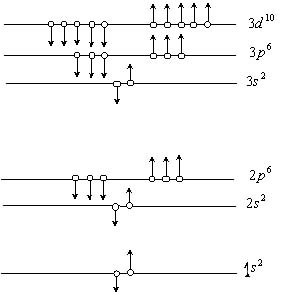Рис. 10.1. Схема расселения электронов по энергетическим уровням в атоме

В классической механике даже одинаковые частицы можно различить по положению в пространстве и импульсам. В квантовой механике положение иное. Из соотношения неопределенности вытекает, что для микрочастиц вообще неприменимо понятие траектории; состояние микрочастицы описывается волновой функцией, позволяющей лишь вычислять вероятность нахождения микрочастицы в окрестностях той или иной точки пространства. Если же волновые функции двух тождественных частиц в пространстве перекрываются, то разговор о том, какая частица находится в данной области, вообще лишен смысла: можно говорить лишь о вероятности нахождения в данной области одной из тождественных частиц. Таким образом, в квантовой механике тождественные частицы полностью теряют свою индивидуальность и становятся неразличимыми.

Если при перемене частиц местами волновая функция не меняет знака, то она называется симметричной, если меняет – антисимметричной. Изменение знака волновой функции не означает изменения состояния, т.к. физический смысл имеет лишь квадрат модуля волновой функции.

Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса: частицы с полуцелым спином (например электроны, нейтроны и протоны) описываются антисимметричными волновыми функциями и подчиняются статистике Ферми–Дирака; эти частицы называются фермионами. Частицы с нулевым, или целочисленным, спином (например фотоны, мезоны) описываются симметричными функциями (волновыми) и подчиняются статистике Бозе–Эйнштейна; эти частицы называются бозонами.

Сложные частицы (например атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спин – полуцелый), а из четного – бозонами (суммарный спин – целый).

Распределение электронов по различным квантовым состояниям подчиняется принципу Паули, согласно которому в одном состоянии не может быть двух одинаковых (с одинаковым набором четырех квантовых чисел) электронов, они должны отличаться какой-то характеристикой, например направлением спина. Следовательно, по квантовой теории, электроны в металле не могут располагаться на самом низшем энергетическом уровне даже при 0 К. Согласно принципу Паули, электроны вынуждены взбираться вверх «по энергетической лестнице».

Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энергия Ферми E_F, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно отсчитывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых электронами энергетических уровней.

Для металлов при не слишком высоких температурах выполняется неравенство kT < Е_F. Это означает, что электронный газ в металлах практически всегда находится в состоянии сильного вырождения. Температура Т₀ вырождения находится из условия kT₀ = E_F. Она определяет границу, выше которой квантовые эффекты перестают быть существенными. Соответствующие расчеты показывают, что для электронов в металле Т₀ = 10⁴ К, т. е. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден.