Линейный гармонический осциллятор – это система, совершающая одномерное движение под действием квазиупругой силы. Данная модель часто используется во многих задачах классической и квантовой теории. Так, примерами классических гармонических осцилляторов являются пружинный, физический и математический маятники. Потенциальная энергия гармонического осциллятора равна:
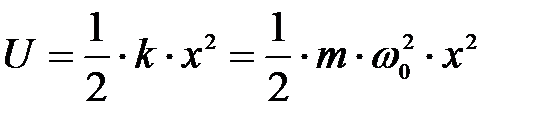, (6.37)
где k – коэффициент жесткости системы; x – отклонение от положения равновесия; w 0 – собственная частота колебаний осциллятора; m – масса колеблющейся системы.
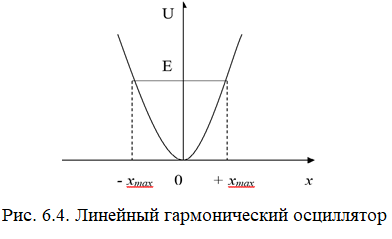Зависимость потенциальной энергии осциллятора от координаты U ( x ) имеет вид «ямы» с параболическими стенками (рис.6.4).
Амплитуда колебаний осциллятора определяется его полной энергией. В точках ± xmax полная энергия равна потенциальной, поэтому с классической точки зрения частица не может выйти за пределы области (от - xmax до + xmax ).
Гармонический осциллятор в квантовой механике описывается стационарным уравнением Шредингера, с учетом вида потенциального поля (6.37):
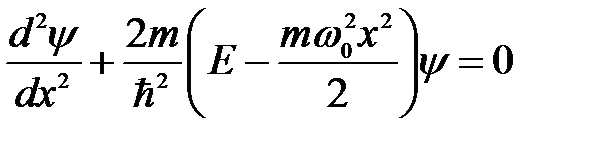. (6.38)
Уравнение (6.38) имеет решение только при собственных значениях энергии:
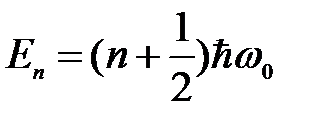( n = 1, 2, 3….). (6.39)
Выражение (6.39) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т.е. энергия квантуется, причем существует минимальная энергия квантового гармонического осциллятора
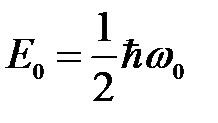. (6.40)
Энергия (6.40) называется энергией нулевых колебаний. Она определяется только собственной частотой осциллятора, ее невозможно отнять у осциллятора никаким охлаждением, она сохранилась бы и при Т = 0 К. Нулевой энергии соответствуют нулевые колебания гармонического осциллятора. Это значит, что частица не может находится на дне «потенциальной ямы». Из соотношения (6.40) следует, что уровни энергии линейного гармонического осциллятора расположены равномерно, то есть, расстояния между соседними уровнями одинаковы и равны:
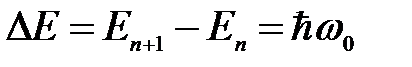. (6.41)
То, что минимальная энергия квантового осциллятора не равна нулю (частица не может находиться на дне потенциальной ямы) связано с принципом неопределенности. Если бы энергия частицы была равна нулю, то частица покоилась бы, и ее импульс и координаты имели бы одновременно определенные значения, что противоречит принципу неопределенности. Наличие нулевой энергии квантового осциллятора подтверждается экспериментально.
Расчеты, выходящие за рамки уравнения Шредингера, показывают, что для квантового осциллятора возможны переходы лишь между соседними стационарными уровнями, при которых квантовое число изменяется на единицу: ∆ n = ± 1. При каждом из этих переходов испускается или поглощается квант энергии ћν.
Примеры решения задач
Задача 1. Показать, что ограничение частицы в пространстве вызывает квантование ее энергии.
Решение
Рассмотрим частицу в одномерной потенциальной яме с бесконечно высокими стенками (см. рис.6.5).
|
| Рис. 6.5 |
Найдем волновую функцию частицы. Для нее мы ожидаем:
·Y (х) = 0 вне ямы;
· Y (0) = Y ( L ) = 0 на стенках ямы;
· Y (х) должна быть волной или суммой волн, т.к. представляет частицу и должна быть связана с деБройлевской волной.
Пусть волновая функция имеет вид:
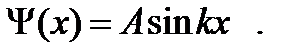
Она должна вписываться в «ящик» (рис.6.6):
|
| Рис.6.6. |
Это означает, что целое число полуволн должно укладываться на длине L
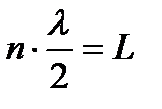
или возможные длины волн равны:
,
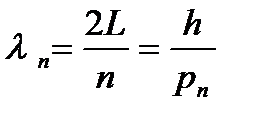где n = 1, 2, 3, …..
Отсюда получаем возможные значения импульсов частицы в яме:
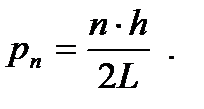
Полная энергия частицы в пределах ямы равна кинетической энергии, т.к. потенциальная энергия в яме U = 0 и частица является свободной:
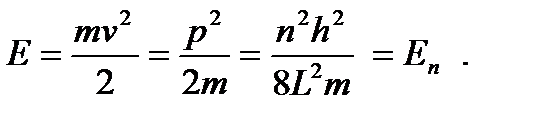
Итак, частица обладает не любой энергией, а вполне конкретной, зависящей от целого числа n
,
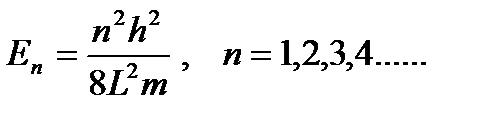где n – главное квантовое число.
Таким образом, действительно ограничение движения частицы в пространстве приводит к квантованию ее энергии. Это же должно быть справедливо и для электрона в атоме водорода.
Отметим, что энергия частицы с Е = 0 отсутствует, т.к. соответствующая ей волна не существует. Таким образом, минимальная энергии частицы в потенциальной яме соответствует состоянию с квантовым числом n=1:
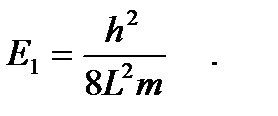
Задача 2. Частица находится в одномерном потенциальном ящике шириной L. Найти среднее положение частицы в основном состоянии.
Решение
По определению средняя координата частицы определяется из соотношения
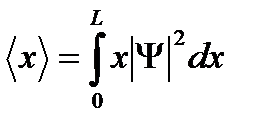
Волновая функция частицы в потенциальной яме (см. предыдущую задачу)
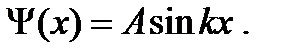
Из требования
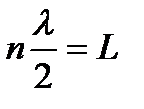
длина волны основного состояния, для которого n = 1, равна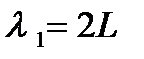 
, а волновой вектор
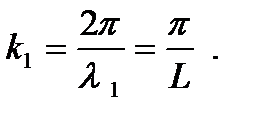
Волновая функция основного состояния имеет вид: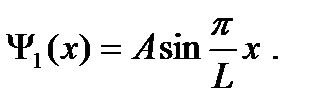 
Волновая функция должна быть нормирована: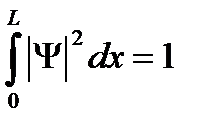 
.
Из условия нормировки находим амплитуду волновой функции А:
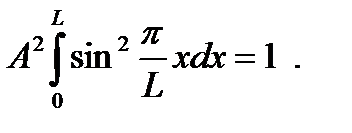
Вычислим интеграл:
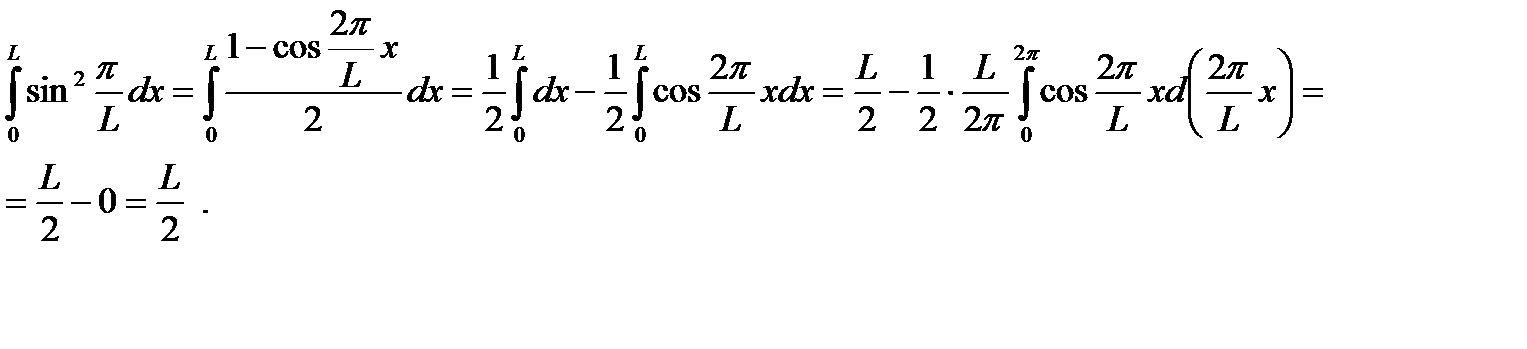
Получаем: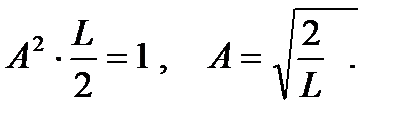 
Итак, волновая функция основного состояния имеет вид:
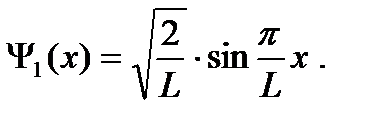
Находим среднюю координату частицы:
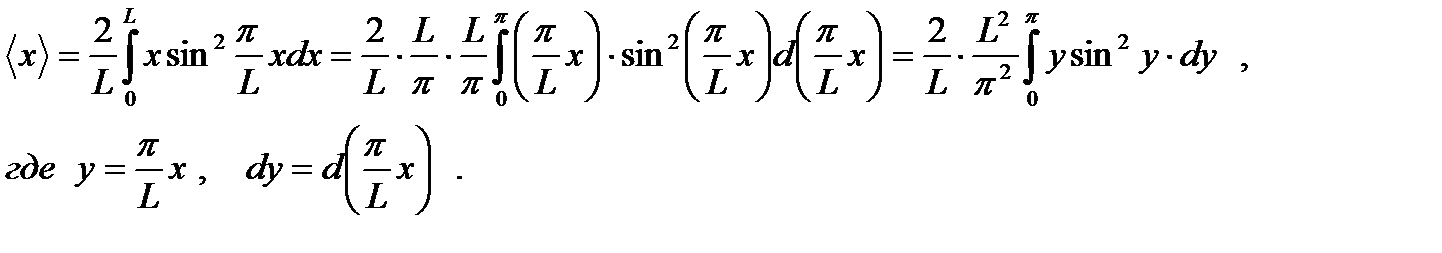
Вычислим интеграл:
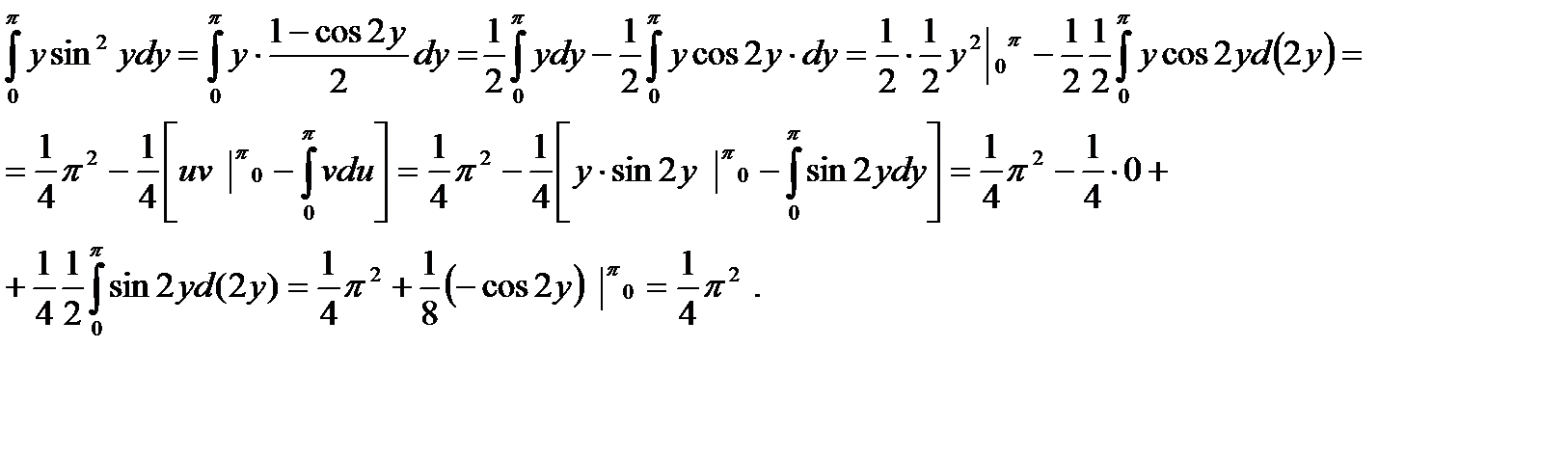
В результате получаем: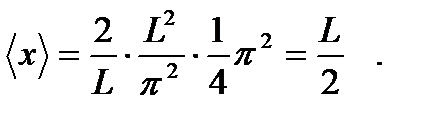 
Видно, что частица находится в середине ящика, что и следует из плотности вероятности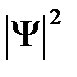 
:
Рис. 6.7.
Задача 3. Какова ширина (l) одномерной потенциальной ямы с бесконечно высокими стенками, если при переходе электрона со второго квантового уровня (n1 = 2) на первый (n2 = 1) излучается фотон с энергией Е = 1 эВ?
| Дано: n1 = 2 n2 = 1 Е = 1 эВ | СИ: 1.6×10-19 Дж |
| l - ? |
Решение
Запишем уравнение для энергии электрона на заданных стационарных уровнях:
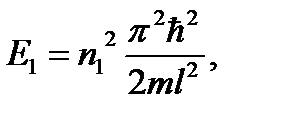
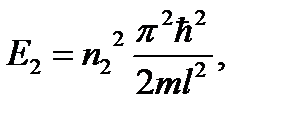
По условию задачи при указанном переходе выделяется квант энергии:
ΔЕ = Е1 – Е2.
Подставим значения соответствующих энергий и получим уравнение:
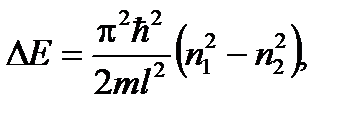
Из последнего уравнения выразим искомую величину – ширину ямы (l):
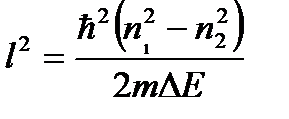
Подставим численные значения и сделаем расчет:
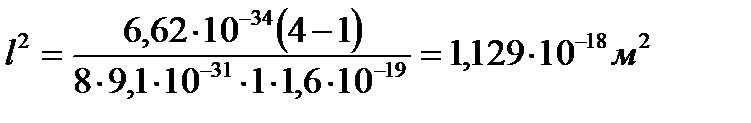
Ответ: l = 1,062 10-9 м.
Задача 4. При какой ширине (l) потенциальной ямы дискретность энергии микрочастицы, находящейся в ней, сравнима с энергией теплового движения при температуре Т.
Решение
Запишем уравнение для собственных энергий электрона в атоме для стационарных уровней с номерами n и (n + 1):
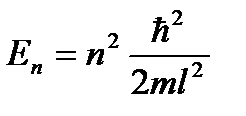и 
Запишем дискретность энергии микрочастицы для указанных состояний с номерами n и (n + 1):
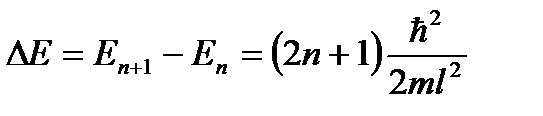
По условию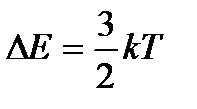 
, поэтому можно записать:
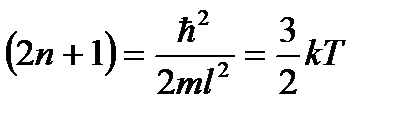
Решаем полученное уравнение относительно ширины ямы – l
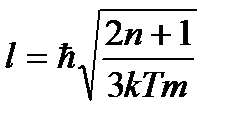
Ответ: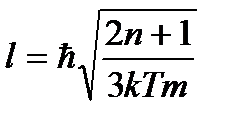 
Задачи для самостоятельного решения
1. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность W нахождения частицы: 1) в средней трети ящика; 2) в крайней трети ящика?
2. Частица в потенциальном ящике шириной L находится в возбуждённом состоянии (n = 2). Определить, в каких точках интервала (0 < x < L) плотность вероятности |ψ n(x)|² нахождения частицы максимальна и минимальна?
3. Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины L с абсолютно непроницаемыми стенками (0<x<L). Найти вероятность пребывания частицы в области 1/3L £x£2/3L.
4. Электрон с длиной волны де Бройля l1 = 100 пм, двигаясь в положительном направлении оси X, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определите длину волны де Бройля после прохождения барьера.
5. Электрон находится в одномерной прямоугольной потенциальной «яме» шириной L с бесконечно высокими стенками. Определите вероятность обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 3).
6. Частица находится в основном состоянии одномерной прямоугольной ямы ширины L с абсолютно непроницаемыми стенками ( 0 < x > L ). Найти вероятность нахождения частицы в области 1/2L < x < 2/3L.
7. Прямоугольный потенциальный барьер имеет ширину L = 0.1 нм. Определите (в эВ) разность энергий U – E, при которой вероятность прохождения электрона сквозь барьер составит 0.5.
8. Частица в одномерной прямоугольной «потенциальной яме» шириной L с бесконечно высокими «стенками» находится в возбужденном состоянии (n= 3). Определите, в каких точках «ямы» плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически.
9. Математический маятник можно рассматривать в качестве гармонического осциллятора. Определите в электрон-вольтах энергию нулевых колебаний маятника длиной l = 1 м, находящегося в поле тяготения Земли.
10. Прямоугольный потенциальный барьер имеет ширину L = 0.1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси x электрона U – E = 5 эВ. Определите, во сколько раз изменится коэффициент прозрачности D потенциального барьера, если разность U – E возрастет в 4 раза.
Практические занятия 8-9
Дата: 2018-12-28, просмотров: 662.
