Н.И.Ильиных, Пилипенко Г.И., Вандышева И.В.
ФИЗИКА (СПЕЦГЛАВЫ)
Методические указания по выполнению практических работ
для студентов очной и заочной форм обучения,
обучающихся по направлению подготовки бакалавра
11.03.02 «Инфокоммуникационные технологии и системы связи»
(профиль «Многоканальные телекоммуникационные системы»)
программа академического бакалавриата
Екатеринбург,
2015
ББК 22.3
УДК 53
Рецензент: доцент кафедры общей физики и естествознания УрГПУ, к.ф.-м.н Сабирзянов А.А.
Ильиных Н.И., Пилипенко Г.И., Вандышева И.В.
Физика (спецглавы): Методические указания по выполнению практических работ /Н.И.Ильиных, Г.И.Пилипенко, И.В.Вандышева. – Екатеринбург: УрТИСИ СибГУТИ, 2015. - 96 с.
Методические указания предназначены для студентов очной и заочной форм обучения, изучающих дисциплину «Физика (спецглавы)» и содержат теоретические сведения, необходимые для решения задач, примеры решения задач, задачи для самостоятельного решения, список необходимой литературы.
Рекомендовано НМС УрТИСИ СибГУТИ в качестве методических указаний по выполнению практических занятий для студентов очной и заочной форм обучения для направления подготовки 11.03.02 «Инфокоммуникационные технологии и системы связи» по профилю: «Многоканальные телекоммуникационные системы», программа академического бакалавриата, квалификация «Бакалавр».
ББК 22.3
УДК 53
Кафедра высшей математики и физики
ã УрТИСИ СибГУТИ, 2015
СОДЕРЖАНИЕ
| Пояснительная записка | 4 |
| Общие методические указания к решению задач | 5 |
| Практическое занятие 1 | 6 |
| Практическое занятие 2 | 16 |
| Практическое занятие 3 | 22 |
| Практическое занятие 4 | 30 |
| Практическое занятие 5 | 41 |
| Практические занятия 6-7 | 48 |
| Практические занятия 8-9 | 64 |
| Практические занятия 10-12 | 72 |
| Практические занятия 13-14 | 84 |
| Список литературы | 96 |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Цель данного учебного пособия - оказать помощь студенту в закреплении теоретических знаний курса «Физика (спецглавы)» и приобретении необходимых навыков решения задач, необходимых при выполнении домашних и контрольных работ.
При создании пособия авторы руководствовались действующей программой курса «Физика (спецглавы)», разработанной на основании требований федерального государственного образовательного стандарта высшего образования по направлению подготовки 11.03.02 «Инфокоммуникационные технологии и системы связи (уровень бакалавриата)» 2015 г.
Пособие содержит методические указания по решению задач, краткое изложение основных положений и тем курса. Приведены примеры решения наиболее типичных задач, а также задачи для самостоятельного решения.
Объем часов, отведенных на проведение каждой работы, а также ее тема указаны в таблице.
Перечень практических работ
| Перечень практических занятий | Количество часов |
| 1. Дисперсия света. Поглощение света. Эффекты Доплера и Вавилова-Черенкова. | 4 |
| 2. Тепловое излучение. Фотоны. Давление света | 4 |
| 3. Внешний фотоэффект. Эффект Комптона | 4 |
| 4. Планетарная модель атома. Строение атома водорода по Бору. Спектры излучения атомов | 4 |
| 5. Корпускулярно-волновой дуализм свойств вещества. Волны де Бройля. Соотношение неопределенностей | 4 |
| 6. Волновая функция. Уравнение Шредингера. | 2 |
| 7. Движение заряженных частиц в потенциальной «яме» с бесконечно высокими «стенками». Туннельный эффект. | 4 |
| 8. Строение атома водорода в квантовой механике. | 2 |
| 9. Принцип запрета Паули. Многоэлектронные атомы | 2 |
| 10. Элементы квантовой статистики | 4 |
| 11. Зонная структура твердых тел | 2 |
| 12. Электропроводность полупроводников. Контактные явления | 2 |
| 13. Закон радиоактивного распада. Ядерные реакции | 4 |
| 14. Фундаментальные взаимодействия. Элементарные частицы | 4 |
| ИТОГО: | 46 |
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К РЕШЕНИЮ ЗАДАЧ
При решении задач необходимо пользоваться следующей схемой:
· Внимательно прочитать условие задачи.
· Выписать столбиком все величины, входящие в условие, и выразить их в одних единицах (преимущественно в Международной системе единиц СИ).
· Если это возможно, представить условие задачи в виде четкого рисунка. Правильно сделанный рисунок – это наполовину решенная задача.
· Уяснить физическую сущность задачи, установить основные законы и формулы, на которых базируется условие задачи.
· Если при решении задачи применяется формула, полученная для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какой-нибудь физической величины, то ее следует вывести.
· Решить задачу сначала в общем виде, то есть, в буквенных обозначениях, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин
· После получения расчетной формулы для проверки ее правильности следует подставить в правую часть формулы вместо символов величин их размерности, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.
· Подставить в конечную формулу числовые значения, выраженные в единицах СИ. В виде исключения допускается выражать в любых, но одинаковых единицах числовые значения однородных величин, стоящих в числителе и знаменателе дроби и имеющих одинаковые степени.
· При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 3520 надо записать 3,52×103, вместо 0,00129 записать 1,29×10-3 и т. п.
· Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений. Как правило, окончательный ответ следует записывать с тремя значащими цифрами. Это относится и к случаю, когда результат получен с применением калькулятора.
· Решение задачи должно сопровождаться краткими, но исчерпывающими пояснениями и комментариями.
Практическое занятие 1
Краткая теория.
Дисперсией света называется зависимость показателя преломления л вещества от частоты v (длины волны l) света или зависимость фазовой скорости v световых волн от его частоты n. Дисперсия света представляется в виде зависимости
n = f ( λ ) (1.1)
Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Первые экспериментальные наблюдения дисперсии света принадлежат И. Ньютону (1672 г.).
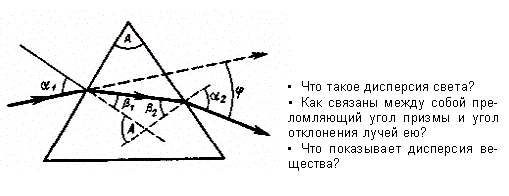
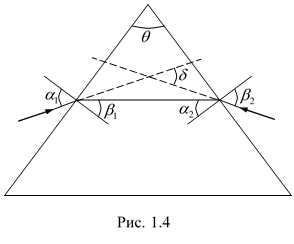
Рассмотрим дисперсию света в призме. Пусть монохроматический пучок света падает на призму с преломляющим углом А и показателем преломления п (рис.1.1) под углом a1. После двукратного преломления (на левой и правой гранях призмы) луч оказывается отклоненным от первоначального направления на угол j.
|
|
Рис.1.1. Дисперсия в призме
Из рисунка следует, что
j = ( a 1 - b 1 ) + ( a 2 - b 2 ) = a 1 + a 2 + A (1.2)
Предположим, что углы А и a1 малы, тогда углы a2, b1 и b2 будут также малы и вместо синусов этих углов можно воспользоваться их значениями. Поэтому a 1 / b 1 = n , b 2 / a 2 = 1/ n, а так как b 1 + b 2 = A , то a 2 = b 2 n = n ( A - b 1 ) = n ( A - a 1 / n ) = nA - a 1 , откуда
a 1 + a 2 = nA (1.3)
Из выражений (1.3) и (1.2) следует, что
j = A ( n -1) (1.4)
т. е. угол отклонения лучей призмой тем больше, чем больше преломляющий угол призмы.
Из выражения (1.4) следует, что угол отклонения лучей призмой зависит от величины (n – 1), а n - функция длины волны, поэтому лучи разных длин волн после прохождения призмы окажутся отклоненными на разные углы, т. е. пучок белого света за призмой разлагается в спектр, что и наблюдалось И.Ньютоном. Таким образом, с помощью призмы, так же, как и с помощью дифракционной решетки, разлагая свет в спектр, можно определить его спектральный состав.
Рассмотрим различия в дифракционном и призматическом спектрах.
1. Дифракционная решетка разлагает падающий свет непосредственно по длинам волн, поэтому по измеренным углам (по направлениям соответствующих максимумов) можно вычислить длину волны. Разложение света в спектр в призме происходит по значениям показателя преломления, поэтому для определения длины волны света надо знать зависимость n = ¦(l).
2. Составные цвета в дифракционном и призматическом спектрах располагаются различно. В дифракционной решетке синус угла отклонения пропорционален длине волны. Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи в спектр по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны уменьшается (рис. 1.1). Поэтому красные лучи отклоняются призмой слабее, чем фиолетовые.
Величина D = dn / dλ, называемая дисперсией вещества, показывает, как быстро изменяется показатель преломления с длиной волны. Дисперсия света называется нормальной, если показатель преломления монотонно возрастает с увеличением частоты (убывает с увеличением длины волны); в противном случае дисперсия света называется аномальной (Рис.1.2). Нормальная дисперсия света наблюдается вдали от собственных линий поглощения, аномальная – в пределах полос или линий поглощения.
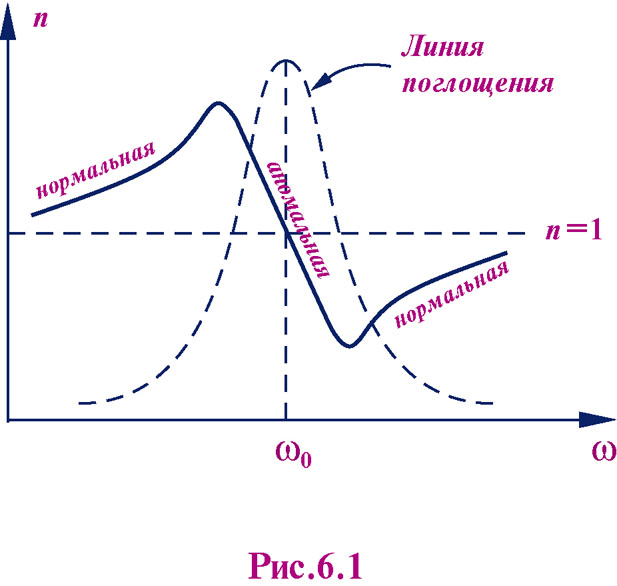
Рис.1.2. Зависимость показателя преломления вещества от частоты.
На явлении нормальной дисперсии основано действие призменных спектрографов. Несмотря на их некоторые недостатки (например, необходимость градуировки, различная дисперсия в разных участках спектра) при определении спектрального состава света, призменные спектрографы находят широкое применение в спектральном анализе. Это объясняется тем, что изготовление хороших призм значительно проще, чем изготовление хороших дифракционных решеток. В призменных спектрографах также легче получить большую светосилу.
Из макроскопической электромагнитной теории Максвелла следует, что абсолютный показатель преломления среды 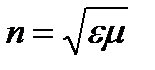 , где e - диэлектрическая проницаемость среды, m - магнитная проницаемость. В оптической области спектра для всех веществ m » 1, поэтому
, где e - диэлектрическая проницаемость среды, m - магнитная проницаемость. В оптической области спектра для всех веществ m » 1, поэтому
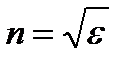 (1.5)
(1.5)
Из формулы (1.5) выявляются некоторые противоречия с опытом: величина n , являясь переменной, остается в то же время равной определенной постоянной 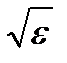 . Кроме того, значения n, получаемые из этого выражения, не согласуются с опытными значениями. Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны.
. Кроме того, значения n, получаемые из этого выражения, не согласуются с опытными значениями. Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны.
Поглощением (абсорбцией) света называется явление уменьшения энергии световой волны при ее распространении в веществе вследствие преобразования энергии волны в другие виды энергии. В результате поглощения интенсивность света при прохождении через вещество уменьшается.
Поглощение света в веществе описывается законом Бугера:
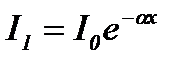 (1.6)
(1.6)
где I0 и I - интенсивности плоской монохроматической световой волны на входе и выходе слоя поглощающего вещества толщиной х, a - коэффициент поглощения, зависящий от длины волны света, химической природы и состояния вещества и не зависящий от интенсивности света. При х=1/a интенсивность света I по сравнению с I0 уменьшается в е раз.
Коэффициент поглощения зависит от длины волны l (или частоты w) и для различных веществ различен. Например, одноатомные газы и пары металлов (т. е. вещества, в которых атомы расположены на значительных расстояниях друг от друга и их можно считать изолированными) обладают близким к нулю коэффициентом поглощения и лишь для очень узких спектральных областей (примерно 10-12 - 10-7 м) наблюдаются резкие максимумы (так называемый линейчатый спектр поглощения). Эти линии соответствуют частотам собственных колебаний электронов в атомах. Спектр поглощения молекул, определяемый колебаниями атомов в молекулах, характеризуется полосами поглощения (примерно 10~10-10~7 м).
Коэффициент поглощения для диэлектриков невелик (примерно 10-3 - 10-5 см-1), однако у них наблюдается селективное поглощение света в определенных интервалах длин волн, когда α резко возрастает, и наблюдаются сравнительно широкие полосы поглощения, т. е. диэлектрики имеют сплошной спектр поглощения. Это связано с тем, что в диэлектриках нет свободных электронов и поглощение света обусловлено явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика.
Коэффициент поглощения для металлов имеет большие значения (примерно 103 -105 см-1) и поэтому металлы являются непрозрачными для света. В металлах из-за наличия свободных электронов, движущихся под действием электрического поля световой волны, возникают быстропеременные токи, сопровождающиеся выделением Джоулевой теплоты. Поэтому энергия световой волны быстро уменьшается, превращаясь во внутреннюю энергию металла. Чем выше проводимость металла, тем сильнее в нем поглощение света.
На рис. 1.3 представлены типичная зависимость коэффициента поглощения a от длины волны света l и зависимость показателя преломления n от l в области полосы поглощения. Из рисунка следует, что внутри полосы поглощения наблюдается аномальная дисперсия (n убывает с уменьшением l). Однако поглощение вещества должно быть значительным, чтобы повлиять на ход показателя преломления.
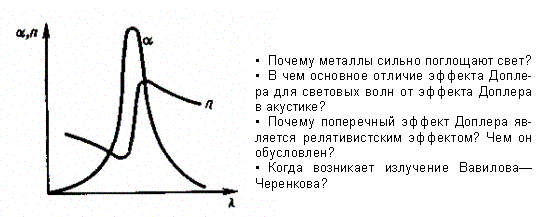
Рис.1.3. Зависимость коэффициента поглощения и показателя преломления от длины волны света
Зависимостью коэффициента поглощения от длины волны объясняется окрашенность поглощающих тел.
Например, стекло, слабо поглощающее красные и оранжевые лучи и сильно поглощающее зеленые и синие, при освещении белым светом будет казаться красным. Если на такое стекло направить зеленый и синий свет, то из-за сильного поглощения света этих длин волн стекло будет казаться черным. Это явление используется для изготовления светофильтров, которые в зависимости от химического состава (стекла с присадками различных солей, пленки из пластмасс, содержащие красители, растворы красителей и т. д.) пропускают свет только определенных длин волн, поглощая остальные. Разнообразие пределов селективного (избирательного) поглощения у различных веществ объясняет разнообразие и богатство цветов и красок, наблюдающееся в окружающем мире.
Явление поглощения широко используется в абсорбционном спектральном анализе смеси газов, основанном на измерениях спектров частот и интенсивностей линий (полос) поглощения. Структура спектров поглощения определяется составом и строением молекул, поэтому изучение спектров поглощения является одним из основных методов количественного и качественного исследования веществ.
Эффект Доплера в акустике объясняется тем, что частота колебаний, воспринимаемых приемником, определяется скоростями движения источника колебаний и приемника относительно среды, в которой происходит распространение звуковых воли. Эффект Доплера наблюдается также и при движении относительно друг друга источника и приемника электромагнитных волн. Так как особой среды, служащей носителем электромагнитных волн, не существует, то частота световых волн, воспринимаемых приемником (наблюдателем), определяется только относительной скоростью источника и приемника (наблюдателя). Закономерности эффекта Доплера для электромагнитных волн устанавливаются на основе специальной теории относительности.
Согласно принципу относительности Эйнштейна, уравнение световой волны во всех инерциальных системах отсчета одинаково по форме. Используя преобразования Лоренца, можно получить уравнение волны, посылаемой источником, в направлении приемника в другой инерциальной системе отсчета, а, следовательно, и связать частоты световых волн, излучаемых источником (v 0) и воспринимаемых приемником (v). Теория относительности приводит к следующей формуле, описывающей эффект Доплера для электромагнитных волн в вакууме:
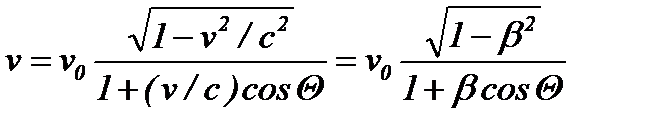 (1.7)
(1.7)
где v - скорость источника света относительно приемника, с - скорость света в вакууме, b = v/c, q - угол между вектором скорости v и направлением наблюдения, измеряемый в системе отсчета, связанной с наблюдателем. Из выражения (1.7) следует, что при q = 0
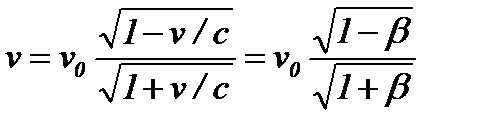 (1.8)
(1.8)
Формула (5.8) определяет так называемый продольный эффект Доплера, наблюдаемый при движении приемника вдоль линии, соединяющей его с источником.
Продольный эффект Доплера был впервые обнаружен в 1900 г. в лабораторных условиях русским астрофизиком А. А. Белопольским (1854-1934) и повторен в 1907 г. русским физиком Б. Б. Голицыным (1862-1919). Продольный эффект Доплера используется при исследовании атомов, молекул, а также космических тел, так как по смещению частоты световых колебаний, которое проявляется в виде смещения или уширения спектральных линий, определяется характер движения излучающих частиц или излучающих тел. Эффект Доплера получил широкое распространение в радиотехнике и радиолокации, например, в радиолокационных измерениях расстояний до движущихся объектов.
Российский физик П. А. Черенков (1904-1990), работавший под руководством Вавилова, показал, что при движении релятивистских заряженных частиц в среде с постоянной скоростью V , превышающей фазовую скорость света в этой среде, т. е. при условии V > c/n (n - показатель преломления среды), возникает электромагнитное излучение, названное впоследствии излучением (эффектом) Вавилова - Черенкова. Природа данного излучения, обнаруженного для разнообразных веществ, в том числе и для чистых жидкостей, подробно изучалась С. И. Вавиловым. Он показал, что данное свечение не является люминесценцией (см. § 245), как считалось ранее, и высказал предположение, что оно связано с движением свободных электронов сквозь вещество.
Излучение Вавилова - Черенкова в 1937 г. было теоретически объяснено российскими учеными И. Е. Таммом (1895-1971) и И. М. Франком (р. 1908) (Черенков, Тамм и Франк в 1958 г. удостоены Нобелевской премии).
Согласно электромагнитной теории, заряженная частица (например, электрон) излучает электромагнитные волны лишь при движении с ускорением. Тамм и Франк показали, что это утверждение справедливо только до тех пор, пока скорость заряжен ной частицы не превышает фазовой скорости с/n электромагнитных волн в среде, в которой частица движется. Если частица обладает скоростью V > c / n, то, даже двигаясь равномерно, она будет излучать электромагнитные волны. Таким образом, согласно теории Тамма и Франка, электрон, движущийся в прозрачной среде со скоростью, превышающей фазовую скорость света в данной среде, должен сам излучать свет.
Отличительной особенностью излучения Вавилова - Черенкова является его распространение не по всем направлениям, а лишь по направлениям, составляющим острый угол q с траекторией частицы, т. е. вдоль образующих конуса, ось которого совпадает с направлением скорости частицы. Определим угол:
cos q = ( c / n )/ v = c /( nv ) (1.9)
Возникновение излучения Вавилова - Черенкова и его направленность истолкованы Франком и Таммом на основе представлений об интерференции света с использованием принципа Гюйгенса.
На основе излучения Вавилова - Черенкова разработаны широко используемые экспериментальные методы для регистрации частиц высоких энергий и определения их свойств (направление движения, величина и знак заряда, энергия). Счетчики для регистрации заряженных частиц, в которых используется излучение Вавилова - Черенкова, получили название черенковских счетчиков. В этих счетчиках частица регистрируется практически мгновенно (при движении заряженной частицы в среде со скоростью, превышающей фазовую скорость света в данной среде, возникает световая вспышка, преобразуемая с помощью фотоэлектронного умножителя в им пульс тока). Это позволило в 1955 г. итальянскому физику Э. Сегре (р. 1905) открыть в черенковском счетчике короткоживущую античастицу - антипротон.
Примеры решения задач.
Задача 1. На грань стеклянной призмы с преломляющим углом 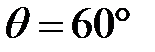 падает луч света под углом
падает луч света под углом 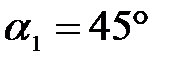 (рис. 20). Найти угол преломления
(рис. 20). Найти угол преломления 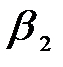 луча при выходе из призмы и угол отклонения
луча при выходе из призмы и угол отклонения 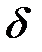 луча от первоначального направления.
луча от первоначального направления.
Дано:
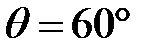
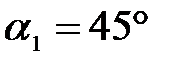
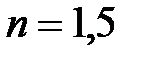
| Си:
|
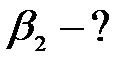
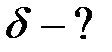
|
Решение:
Угол отклонения луча от первоначального направления
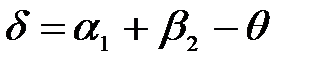 , где
, где 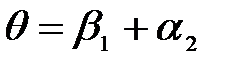 .
.
Согласно закону преломления:
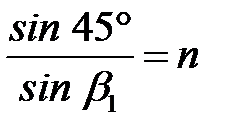 ;
; 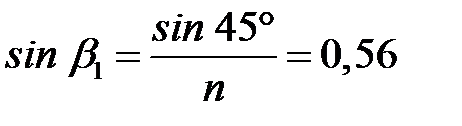 ;
;
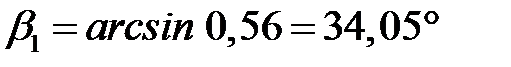 .
.
Из рис.1.4 видно, что
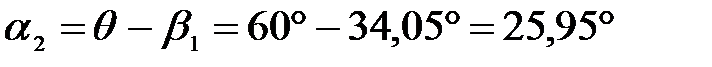 .
.
Согласно закону преломления:
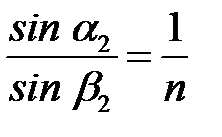 ,
, 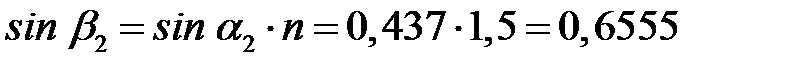 ,
,
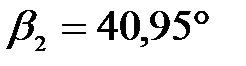 ,
, 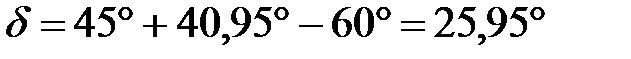 .
.
Ответ: 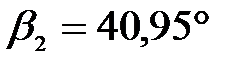 ,
, 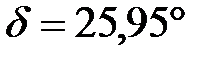 .
.
Задача 2. Монохроматический свет падает поочередно на две пластинки, изготовленные из одного и того же материала, одна толщиной d1 = 4 мм, другая – d2 = 8.5 мм. Пренебрегая вторичными отражениями, определите коэффициент поглощения a этого материала, если первая пластина пропускает h1=0.7 светового потока, а вторая - h1=0.52.
| Дано: d1 = 4 мм d2 = 8.5 мм h1 = 0.7 h1=0.52 | СИ: 4∙10-3 м 8.5∙10-3 м
|
| a - ? |
Решение.
Запишем за кон Бугера:
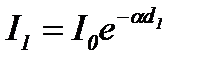
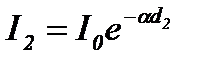
где I0, I1, I2 – интенсивности света на входе и выходе первой и второй пластинки.
По условию задачи: h1 = I1/I0, h2 = I2/I0. Следовательно,
h1/h2 = I1/I2 = ea(d2 – d1).
Прологарифмировав левую и правую части последнего уравнения, получаем:
ln(h1/h2) = a(d2 – d1).
Отсюда:
a = ln(h1/h2)/ (d2 – d1).
Подставим численные значения, проведем расчет, получаем:
a = ln(0.7/0.52)/(8.5 – 4) = 0.661 мм-1.
Ответ: a = 0.661 мм-1.
Задачи для самостоятельного решения
1. Показатель преломления материала призмы для некоторого монохроматического луча равен 1,6. Каков должен быть наибольший угол α1 падения этого луча на призму, чтобы при выходе луча из нее не наступило внутреннее отражение? Преломляющий угол призмы 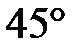 .
.
2. На грань стеклянной призмы (n = 1,5) нормально падает луч света. Определить угол отклонения луча призмой, если ее преломляющий угол равен 25°.
3. При прохождении света в некотором веществе пути х его интенсивность уменьшилась в два раза. Определить, во сколько раз уменьшится интенсивность света при прохождении им пути 4p.
4. Коэффициент поглощения некоторого вещества для монохроматического света определенной длины волны равен a = 0.1 см-1. Определить толщину слоя вещества, которая необходима для ослабления света в 2 раза. Потери на отражение света не учитывать.
5. Коэффициент поглощения графита для монохроматического света определенной длины волны a = 700 см-1. Определите толщину слоя графита, вызывающего ослабление света в 100 раз.
6. Источник монохроматического света с длиной волны l0 =0,6 мкм движется по направлению к наблюдателю со скоростью v = 0.15 с (с - скорость света в вакууме). Определить длину волны l, которую зарегистрирует приемник.
7. Определить минимальную кинетическую энергию (в мегаэлектрон-вольтах), которой должен обладать электрон, чтобы в среде с показателем преломления n = 1,5 возникло излучение Вавилова - Черенкова.
8. Скорость распространения электромагнитных волн в некоторой среде равна 2.5∙108 м/с. Определите длину волны электромагнитных волн в этой среде, если их частота в вакууме равна 1 МГц.
9. Определите скорость распространения электромагнитных волн в парафине, если его диэлектрическая проницаемость ε=2 и магнитная проницаемость μ=1.
10. Определите скорость движения туманности относительно Земли, если линия атомарного водорода с длиной волны λ0 = 656.3 нм в спектре туманности испытывает доплеровское смещение на Dλ = 1.2 нм.
Практическое занятие 2
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Квантовая природа излучения. Фотоны. Давление света»
2. Привитие навыков решения задач по данной теме.
Краткая теория
Тепловое излучение – излучение электромагнитных волн, происходящее за счет внутренней энергии тел, т.е. энергии теплового движения атомов и молекул. Все остальные виды излучения называются люминесценцией. В тепловом излучении участвуют все тела в природе, оно происходит при любых температурах. В отличие от других видов излучения, тепловое излучение является равновесным, т.к. испускание фотонов атомами или молекулами происходит в условиях термодинамического равновесия в среде. При изменении температуры среды меняется интенсивность излучения.
Характеристики теплового излучения:
Энергетическая светимость  - СФВ, численно равная энергии, излучаемой единицей площади поверхности тела за единицу времени по всем направлениям
- СФВ, численно равная энергии, излучаемой единицей площади поверхности тела за единицу времени по всем направлениям
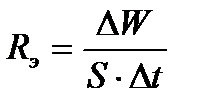 , (2.1)
, (2.1)
где 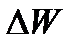 - энергия, излученная телом,
- энергия, излученная телом, 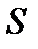 - площадь поверхности тела,
- площадь поверхности тела, 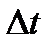 - время излучения.
- время излучения.
Спектральная излучательная (испускательная) способность 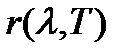 (спектральная плотность энергетической светимости) - СФВ, характеризующая распределение излучаемой энергии по длинам волн. С энергетической светимостью эта величина связана соотношением
(спектральная плотность энергетической светимости) - СФВ, характеризующая распределение излучаемой энергии по длинам волн. С энергетической светимостью эта величина связана соотношением
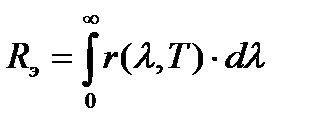 . (2.2)
. (2.2)
Спектральная поглощательная способность (коэффициент поглощения) 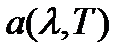 - СФВ, характеризующая распределение поглощенной энергии по длинам волн
- СФВ, характеризующая распределение поглощенной энергии по длинам волн
 , (2.3)
, (2.3)
где 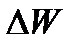 - падающая на тело энергия,
- падающая на тело энергия, 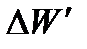 - поглощенная энергия. По значению спектральной поглощательной способности различают следующие модели:
- поглощенная энергия. По значению спектральной поглощательной способности различают следующие модели:
1) абсолютно черное тело (АЧТ) – тело, которое поглощает всю падающую на него энергию ( 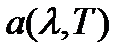
 1);
1);
2) абсолютно белое тело –– тело, которое полностью отражает всю падающую энергию ( 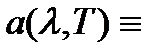 0);
0);
3) серое тело – тело, у которого коэффициент поглощения остается постоянным, но меньшим 1, в широком интервале температур и длин волн ( 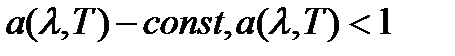 ).
).
Для тел, участвующих в тепловом излучении, справедлив закон Кирхгофа: отношение спектральной излучательной способности к спектральной поглощательной способности есть универсальная функция, единая для всех тел
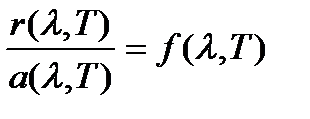 . (2.4)
. (2.4)
|
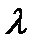
|
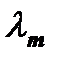
|
| Рис.2.1. |
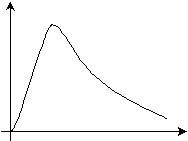
Явный вид универсальной функции Кирхгофа можно установить, если изучить спектральную излучательную способность АЧТ. Экспериментально полученная зависимость
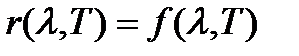 представлена на рис.2.1.
представлена на рис.2.1.
Законы излучения АЧТ:
Закон Стефана-Больцмана устанавливает связь между интегральной энергетической светимостью абсолютно черного тела и его температурой: энергетическая светимость АЧТ пропорциональна его термодинамической температуре 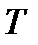 в четвертой степени:
в четвертой степени:
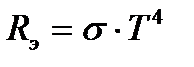 , (2.5)
, (2.5)
где 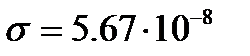
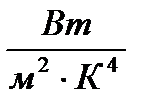 - постоянная Стефана-Больцмана.
- постоянная Стефана-Больцмана.
Закон смещения Вина: Длина волны, соответствующая максимуму спектральной плотности энергетической светимости ЧТ, обратно пропорциональна его термодинамической температуре:
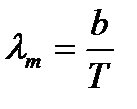 , (2.6)
, (2.6)
где 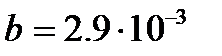
 - постоянная Вина.
- постоянная Вина.
Классическая физика оказалась не в состоянии объяснить закономерности теплового излучения. Это было сделано М. Планком, который предположил, что свет излучается порциями – квантами. Гипотеза Планка положила начало развитию квантовой физики.
Фотон ‑ квант электромагнитного излучения, обладающий энергией, импульсом и гравитационной массой.
Энергия кванта света (фотона) определяется его частотой n:
 , (2.7)
, (2.7)
где 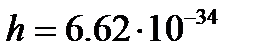
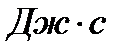 - постоянная Планка,
- постоянная Планка,  ‑ частота колебания векторов напряженности
‑ частота колебания векторов напряженности  и
и  электромагнитного поля излучения;
электромагнитного поля излучения;  - длина волны;
- длина волны;  - циклическая частота колебаний. В расчетах часто пользуются усеченной постоянной Планка
- циклическая частота колебаний. В расчетах часто пользуются усеченной постоянной Планка
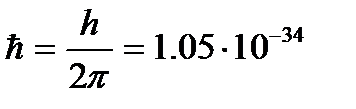
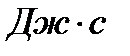 . (2.8)
. (2.8)
Масса фотона
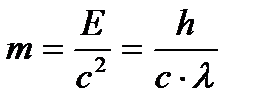 , (2.9)
, (2.9)
где с = 3∙108 м/c - скорость света в вакууме; l — длина волны фотона,
Импульс  фотона в вакууме:
фотона в вакууме:
 ,
,  , (2.10)
, (2.10)
где  - волновой вектор,
- волновой вектор,  .
.
Давление света на поверхность равно импульсу, который передают поверхности N фотонов в течение 1 с:
Р = Nh n / c . (2.11)
Если в единицу времени на единицу площади поверхности падает N фотонов, то от поверхности отразится r N фотонов, а поглотится (1 - r)N фотонов (r - коэффициент отражения). Каждый поглощенный фотон передает поверхности импульс Р = h n / c , а каждый отраженный фотон – импульс 2Р = 2 h n / c . Поэтому общее давление равно:
Р = Nh n / c ( r + 1), (2.12)
где Nh n = Ее – это энергия всех фотонов, падающих на единицу поверхности за единицу времени, то есть, энергетическая освещенность поверхности. Следовательно, давление света равно:
Р = Ее/ c ( r + 1) = w ( r + 1), (2.13)
где w = Ee / c – объемная плотность энергии излучения.
Примеры решения задач
Задача 1. Определить энергию  , излучаемую за время
, излучаемую за время  мин. из смотрового окошка площадью
мин. из смотрового окошка площадью 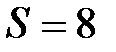 см2 плавильной печи, если её температура
см2 плавильной печи, если её температура 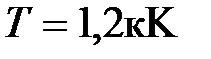 .
.
Дано:
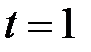 мин. мин.
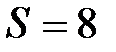 см2 см2
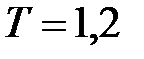 кК кК
| Си: 60 с 8·10-4 м2 1,2·103 К
|

|
Решение:
Согласно закону Стефана-Больцмана энергетическая светимость абсолютно чёрного тела пропорциональна 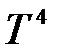 :
:
 ,
,
где  Вт/(м2·К4) – постоянная Стефана-Больцмана.
Вт/(м2·К4) – постоянная Стефана-Больцмана.
С другой стороны, Rе – это энергия, излучаемая за единицу времени единицей поверхности абсолютно черного тела: 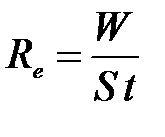 .
.
Тогда энергия, излучаемая за время t: 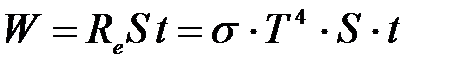 .
.
Произведем вычисления:
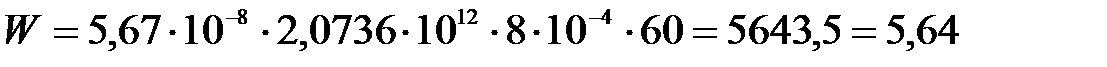 (кДж).
(кДж).
Ответ: 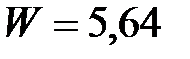 кДж.
кДж.
Задача 2. Можно условно принять, что Земля излучает как серое тело, находящееся при температуре 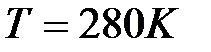 . Определить коэффициент теплового излучения ат Земли, если энергетическая светимость
. Определить коэффициент теплового излучения ат Земли, если энергетическая светимость 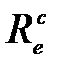 её поверхности равна 325 кДж/(м2·ч).
её поверхности равна 325 кДж/(м2·ч).
Дано:
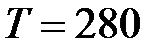 К К
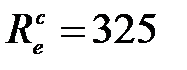 кДж/(м2×ч) кДж/(м2×ч)
| Си:
90.278Дж/(м2×c) |
| ат - ? |
Решение:
Земля излучает как серое тело. Коэффициент теплового излучения (степень черноты) серого тела есть отношение энергетической светимости серого тела к энергетической светимости черного тела, и находится по формуле: 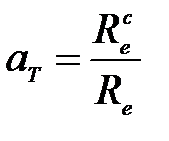 .
.
Закон Стефана-Больцмана для абсолютно чёрного тела, как если бы Земля была абсолютно чёрным телом: 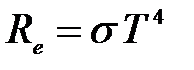 , где
, где 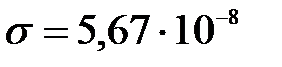 Вт/(м2·К4) – постоянная Стефана-Больцмана. Подставим в коэффициент теплового излучения:
Вт/(м2·К4) – постоянная Стефана-Больцмана. Подставим в коэффициент теплового излучения:
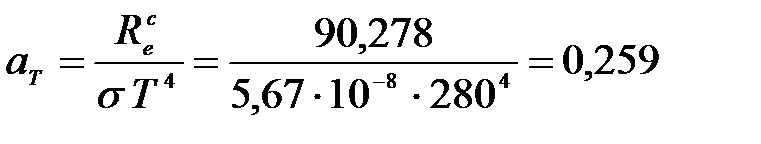 .
.
Ответ: 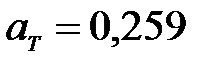 .
.
Задача 3. Излучение Солнца по своему спектральному составу близко к излучению абсолютно черного тела, для которого максимум излучательной способности приходится на длину волны 0.48 мкм. Найти массу, теряемую Солнцем ежесекундно за счет излучения.
Дано:
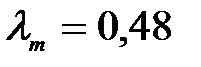 мкм мкм
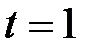 с с
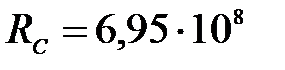 м м
| СИ: 0,48·10-6 м |
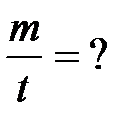
|
Решение:
Теряемую Солнцем массу за любое время найдем из закона Эйнштейна: 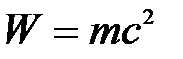 :
:
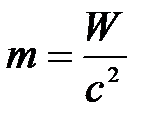 ,
,
где с – скорость света.
Энергия, излучаемая за время t: 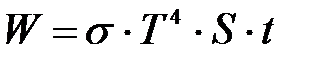 , где , где 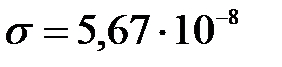 Вт/(м2·К4) – постоянная Стефана-Больцмана. Вт/(м2·К4) – постоянная Стефана-Больцмана.
| ( |
С учетом того, что площадь поверхности Солнца как сферы 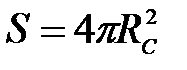 и температура
и температура 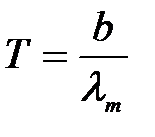 согласно закону смещения Вина, получаем:
согласно закону смещения Вина, получаем:
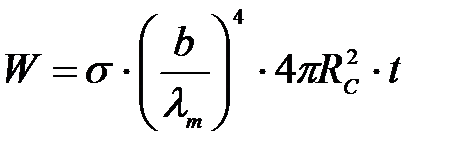 , ,
| ( |
где 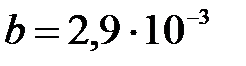 м·К – первая постоянная Вина.
м·К – первая постоянная Вина.
Следовательно: 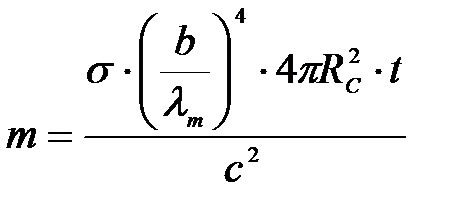 .
.
Масса, теряемая Солнцем ежесекундно: 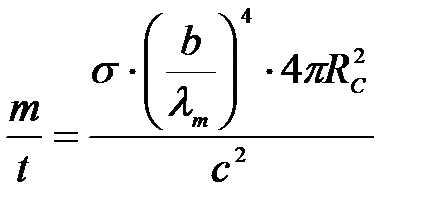 .
.
Подставим численные значения:
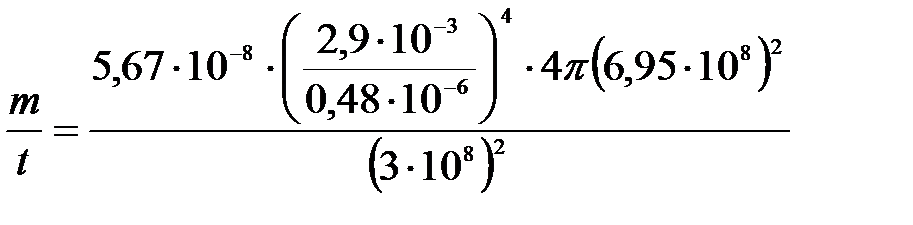 ;
;
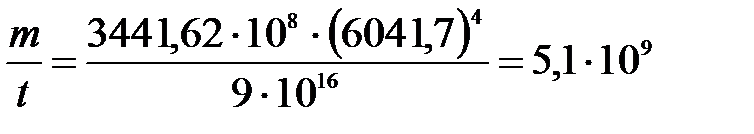 (кг/с).
(кг/с).
Ответ: 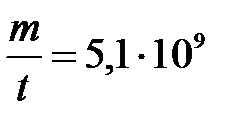 кг/с.
кг/с.
Задача 4. Определить для фотона с длиной волны 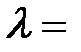 0,5 мкм: 1) его массу (
0,5 мкм: 1) его массу ( 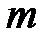 ); 2) энергию (
); 2) энергию (  ); 3) импульс (
); 3) импульс ( 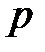 ).
).
| Дано: λ = 0,5 мкм h = 6,626·10-34 Дж·с с = 3·108 м/с е = 1,6·10-19 Кл | СИ: 5×10-7 м |
| 1) m = ? 2) ε = ? 3) р =? |
Решение:
1) 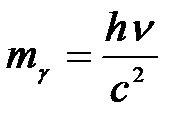 – масса фотона,
– масса фотона,
где 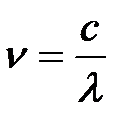 – частота испускания света.
– частота испускания света.
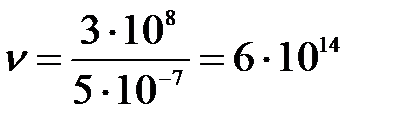 (с-1).
(с-1).
Найдем массу фотона:
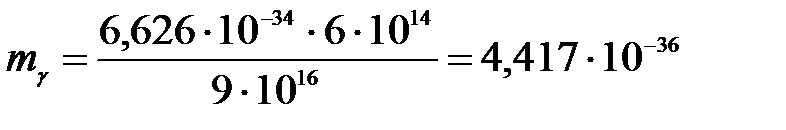 (кг).
(кг).
2) 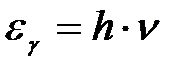 – энергия фотона.
– энергия фотона.
Подставим значения в формулу:
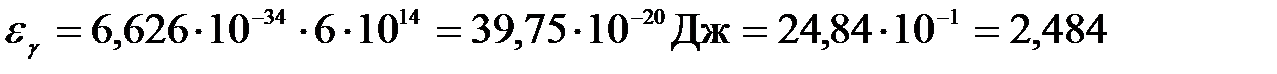 (эВ).
(эВ).
1 эВ = 1,6·10-19 Дж.
3) 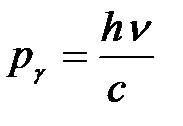 – импульс фотона.
– импульс фотона.
Подставим значения в формулу:
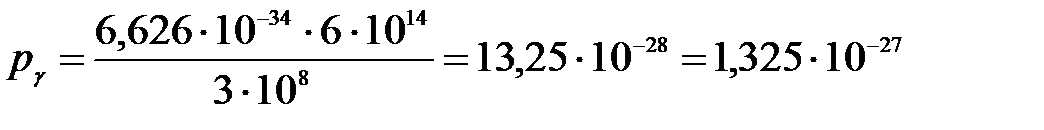 (кг·м/с).
(кг·м/с).
Ответ: 1) m = 4,417·10-36 кг; 2) εγ = 2,484 эВ; 3) рγ = 1,325·10-27 кг·м/с.
Задачи для самостоятельного решения
1. Определить длину волны, на которую приходится максимум энергии в спектре звезды с температурой 30000 К.
2. АЧТ находится при температуре Т1=2900 К. В результате остывания этого тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости изменилась на Dl=9 мкм. До какой температуры Т2 охладили тело?
3. Мощность излучения АЧТ равна 10 КВт. Найти величину излучающей поверхности тела, если известно, что длина волны, на которую приходится максимум спектральной плотности его энергетической светимости, равна 7×10-7м.
4. Какова средняя температура земной поверхности, если длина волны, соответствующая максиму ее теплового излучения, равна 10 мкм?
5. В комнате стоят два одинаковых алюминиевых чайника, содержащих равные количества воды при 90°С. Один из них закоптился и стал черным, а другой остался чистым. Какой из чайников быстрее остынет?
6. Во сколько раз энергия фотона, соответствующего красному свету (l=750нм) отличается от энергии фотона, соответствующего фиолетовому свету (l=400нм)?
7. При нагревании абсолютно черного тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась от 750 нм до 500 нм. Как при этом изменилась энергетическая светимость тела?
8. Поток излучения абсолютно черного тела Ф e = 10 кВт. Максимум энергии излучения приходится на длину волны λ max = 0.8 мкм. Определить площадь S излучающей поверхности.
9. Масса какого из фотонов больше: красного, фиолетового или зеленого?
10. Энергетическая светимость черного тела R=10 кВт/м2. Определите длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела.
Практическое занятие 3
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Внешний фотоэффект. Эффект Комптона»
2. Привитие навыков решения задач по данной теме.
Краткая теория
Фотоэлектрический эффект (фотоэффект) - явление взаимодействия электромагнитного излучения с веществом, в результате которого энергия излучения передаётся электронам вещества. Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом, если не сопровождается – внутренним. С елективный фотоэффект ‑ явление, которое наблюдается у ряда металлов, особенно щелочных, и проявляющееся в том, что кривая зависимости  имеет максимум на частоте собственных колебаний электронов металла (плазмонов). Величина фототока чувствительна к поляризации падающего свет.
имеет максимум на частоте собственных колебаний электронов металла (плазмонов). Величина фототока чувствительна к поляризации падающего свет.
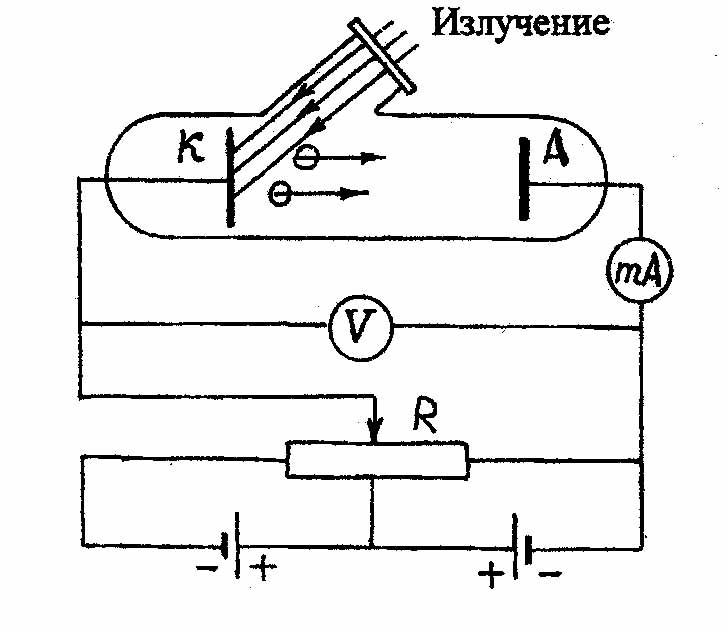
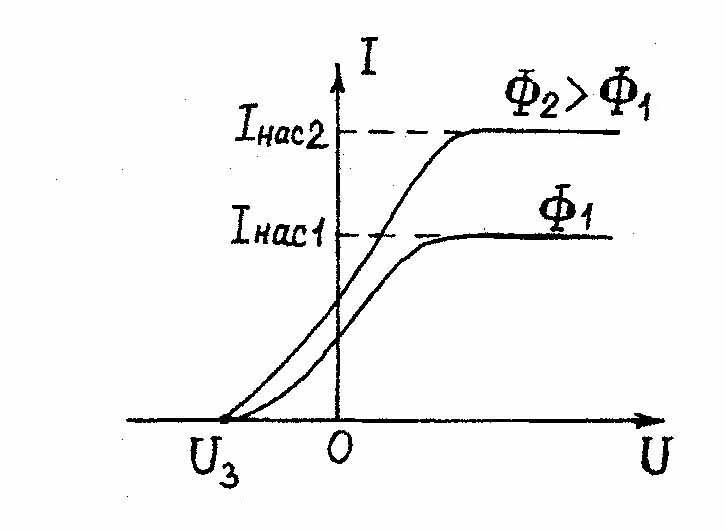
Впервые подробно фотоэффект был исследован русским ученым Столетовым. Схема его экспериментальной установки представлена на рис.3.1.
| 
|
| Рис.3.1. Схема установки для изучения фотоэффекта | Рис.3.2. Вольтамперная характеристика внешнего фотоэффекта. |
Варьируя интенсивность и частоту излучения, а также материал катода, Столетов исследовал зависимость анодного тока от напряжения между катодом и анодом. Типичная вольтамперная кривая показана на рис.3.2.
При изучении вольт - амперных характеристик разнообразных материалов при различных частотах падающего на катод излучения и различных энергетических освещенностях катода в результате обобщения полученных данных были установлены следующие три закона внешнего фотоэффекта (законы Столетова для внешнего фотоэффекта):
1. Сила тока насыщения 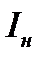 не зависит от длины волны падающего света, а определяется только интенсивностью освещения катода.
не зависит от длины волны падающего света, а определяется только интенсивностью освещения катода.
2. Максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
3. Для каждого вещества существует граничная частота νmin такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения.
Эти законы невозможно объяснить с точки зрения волновой теории света.
А. Эйнштейн в 1905 г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе предложенной им квантовой теории фотоэффекта. Согласно Эйнштейну, свет частотой v не только испускается, как это предполагал Планк, но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых Е = hv. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью с распространения света в вакууме. Кванты электромагнитного излучения получили название фотонов.
По Эйнштейну, каждый квант поглощается только одним электроном.
Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности света (I закон фотоэффекта). Энергия падающего фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии. По закону сохранения энергии:
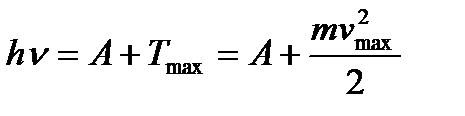 , (3.1)
, (3.1)
где h n - энергия фотона, падающего на поверхность металла; А - работа выхода электрона с поверхности металла; Т max - максимальная кинетическая энергия фотоэлектрона. Для практических целей это уравнения часто записывают в виде
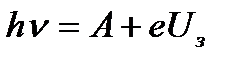 , (3.2)
, (3.2)
где 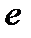 - заряд электрона,
- заряд электрона, 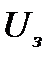 - задерживающее напряжение – напряжение, при котором фототок становится равным нулю.
- задерживающее напряжение – напряжение, при котором фототок становится равным нулю.
Красная граница фотоэффекта наблюдается тогда, когда энергия фотона равна работе выхода, т.е.
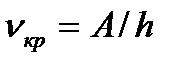 или
или 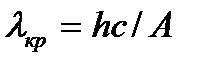 , (3.3)
, (3.3)
где nкр — минимальная частота света, при которой еще возможен фотоэффект; lкр — максимальная длина волны света, при которой еще возможен фотоэффект; h — постоянная Планка; с — скорость света в вакууме. Работа выхода 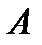 зависит от материала катода и чистоты его поверхности.
зависит от материала катода и чистоты его поверхности.
При высоких частотах используемого излучения на смену фотоэффекту приходит эффект Комптона: при падении на образец рентгеновского излучения с длиной волны 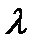 , после образца регистрируется излучение с двумя длинами волн
, после образца регистрируется излучение с двумя длинами волн 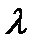 и
и 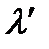 , причем
, причем 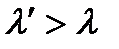 .
.
Экспериментально были установлено, что разность длин волн 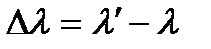 не зависит от материала образца, а определяется лишь углом наблюдения
не зависит от материала образца, а определяется лишь углом наблюдения 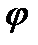 :
:
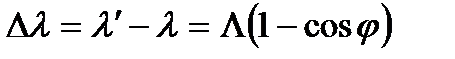 , (3.4)
, (3.4)
где 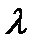 - длина волны фотона, встретившегося со свободным или слабосвязанным электроном;
- длина волны фотона, встретившегося со свободным или слабосвязанным электроном; 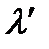 - длина волны фотона, рассеянного на угол j после столкновения с электроном;
- длина волны фотона, рассеянного на угол j после столкновения с электроном; 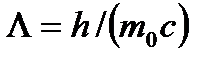 - комптоновская длина волны. Для электрона масса покоя
- комптоновская длина волны. Для электрона масса покоя 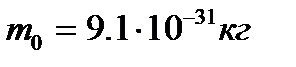 и L=2,436 пм.
и L=2,436 пм.
При увеличении угла 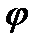 интенсивность излучения с длиной волны
интенсивность излучения с длиной волны 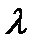 убывает, а с длиной волны
убывает, а с длиной волны 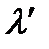 - возрастает. Аналогичная картина наблюдается и при уменьшении порядкового номера исследуемого элемента.
- возрастает. Аналогичная картина наблюдается и при уменьшении порядкового номера исследуемого элемента.
Правильное объяснение эффект Комптона получил лишь в квантовой физике. Здесь считается, что взаимодействие фотона рентгеновского излучения с электроном имеет характер упругого удара и поэтому выполняются законы сохранения импульса и энергии.
Комптоновская длина волны является естественным ограничением в точности определения координаты частицы с помощью электромагнитного излучения.
Излучение черного тела, фотоэффект, эффект Комптона служат доказательством квантовых (корпускулярных) представлений о свете, как о потоке фотонов. С другой стороны, такие явления, как интерференция, дифракция и поляризация света подтверждают волновую (электромагнитную) природу света. Наконец, давление и преломление света объясняются как волновой, так и квантовой теориями. Таким образом, электромагнитное излучение обнаруживает единство, непрерывных (волны) и дискретных (фотоны) свойств, которые взаимно дополняют друг друга.
Примеры решения задач.
Задача 1. Какая доля энергии фотона израсходована на работу вырывания фотоэлектрона, если красная граница фотоэффекта l0 = 307 нм, а максимальная кинетическая энергия 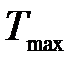 фотоэлектрона равна 1 эВ?
фотоэлектрона равна 1 эВ?
Дано:
l0 = 307 нм
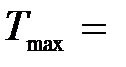 1 эВ
h = 6,63·10-34 Дж·с
с = 3·108 м/с 1 эВ
h = 6,63·10-34 Дж·с
с = 3·108 м/с
| СИ: 307·10-9 м 1,6·10-19 Дж |
|
Решение:
Уравнение Эйнштейна для фотоэффекта – энергия кванта света e расходуется на работу выхода А электрона из вещества и на сообщение кинетической энергии Tmax (скорости) электрону:
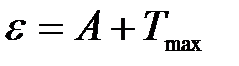 .
.
Работа выхода : 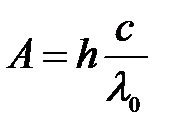 ,
,
где h – постоянная Планка; с – скорость света в вакууме.
Тогда отношение работы выхода к энергии фотона:
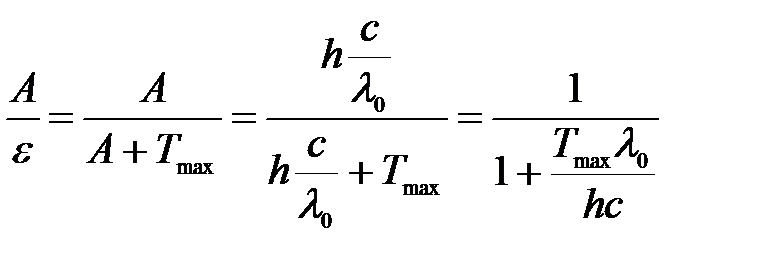 .
.
Вычислим:
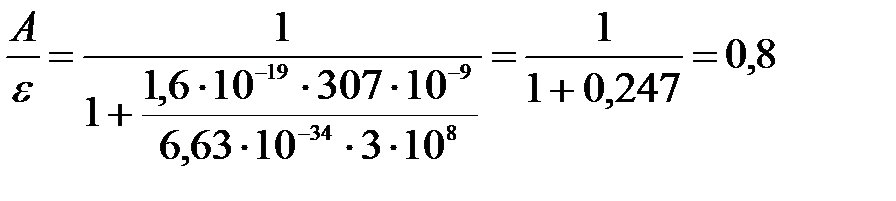 .
.
Ответ: 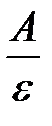 = 0,8.
= 0,8.
Задача 2. Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым светом платиновой пластинки, нужно приложить задерживающую разность потенциалов 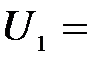 3,7 В; если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придётся увеличить до 6 В. Определить работу А выхода электронов с поверхности этой пластинки.
3,7 В; если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придётся увеличить до 6 В. Определить работу А выхода электронов с поверхности этой пластинки.
| Дано: U1 = 3,7 В U2 = 6 В А1 = 6,3 эВ | СИ: 10,08×10-19 Дж |
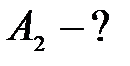
|
Решение:
Согласно уравнению Эйнштейна, при фотоэффекте энергия кванта света (e=h·v) расходуется на работу выхода электрона из вещества А и на сообщение кинетической энергии Т электрону:
e = А + Т.
Кинетическая энергия Т «гасится» работой сил электрического поля Аэл:
Т = Аэл. Учтём, что Аэл = еU. Тогда: 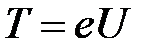 .
.
Тогда для первой и второй пластинки:
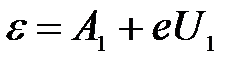 , ,
| |
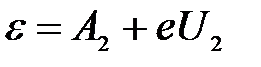 . .
|
Приравняем правые части уравнений:
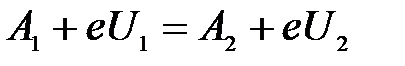 .
.
Выразим интересующую нас работу выхода для второй пластинки:
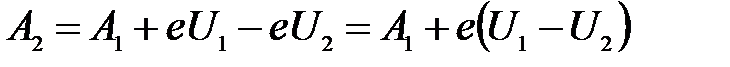 .
.
Подставим числа:
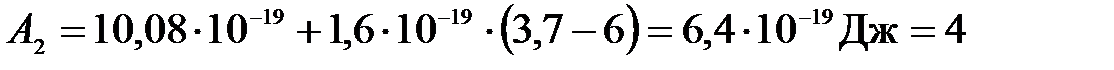 (эВ),
(эВ),
или сразу в электрон-вольтах:
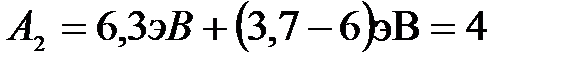 .
.
Ответ: А2 = 4 эВ.
Задача 3. “Красная граница” фотоэффекта для некоторого металла равна 500 нм. Определить: 1) работу выхода электронов из этого металла; 2) максимальную скорость электронов, вырываемых из этого металла светом, с длиной волны 400 нм.
| Дано: λ0 = 500 нм λ = 400 нм h = 6,63·10-34 Дж·с m = 9,11·10-31 кг с = 3·108 м/с | СИ: 5×10-7 м 4×10-7 м |
| 1) Авых = ? 2) υmax = ? |
Решение:
1) Уравнение Эйнштейна для «красной границы» при фотоэффекте:
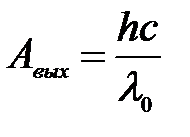 ,
,
где с – скорость света в вакууме, h – постоянная Планка.
Подставим числа:
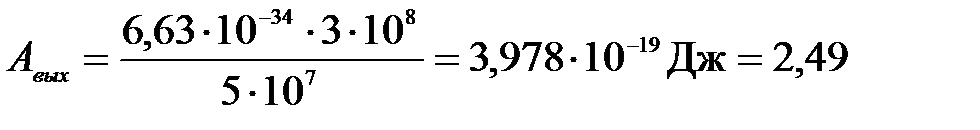 (эВ)
(эВ)
Следует напомнить, что 1 эВ = 1,6·10-19 Дж.
2) Согласно уравнению Эйнштейна, при фотоэффекте энергия кванта света ε расходуется на работу выхода электрона Авых из металла и на сообщение кинетической энергии Т электрону:
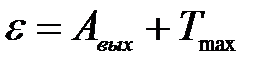 .
.
Энергия фотона: 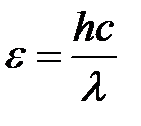 .
.
Кинетическая энергия: 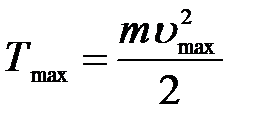 .
.
С учетом всех формул:
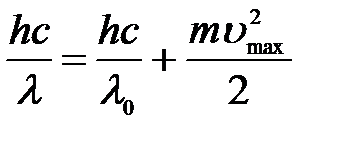 =>
=> 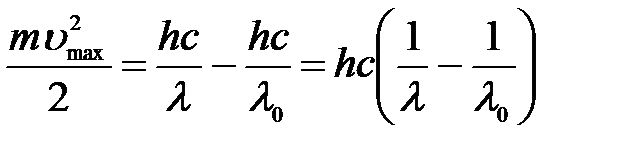 .
.
Откуда максимальная скорость электронов:
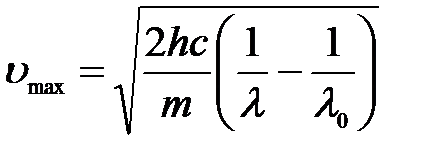 ,
,
где m – это масса электрона.
Подставим числа:
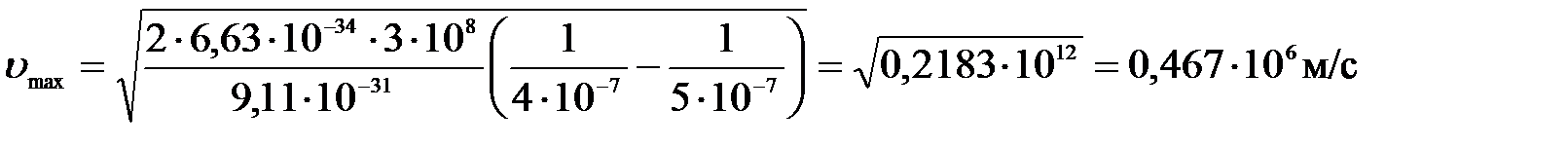 .
.
Ответ: 1) Авых = 2,49 эВ; 2) υmax = 467 км/с.
Задача 4. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпел рассеяние на угол 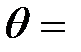 180°? Энергия (
180°? Энергия ( 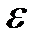 ) фотона до рассеяния равна 0,255 МэВ.
) фотона до рассеяния равна 0,255 МэВ.
Дано:
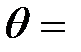 180° 180°
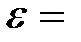 0,255 МэВ
Е0 = 0,511 МэВ 0,255 МэВ
Е0 = 0,511 МэВ
|
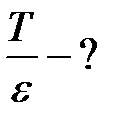
|
Решение:
Закон сохранения энергии:
e = 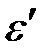 + Т,
+ Т,
где e – энергия падающего фотона, ε/ – энергия рассеянного (отразившегося) фотона, Т – кинетическая энергия электрона.
Выразим кинетическую энергию электрона отдачи Т:
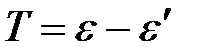 .
.
Тогда отношение кинетической энергии электрона отдачи к энергии падающего фотона:
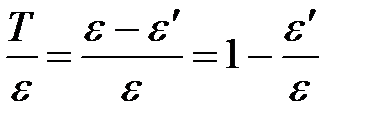 . .
|
Энергия рассеянного фотона: 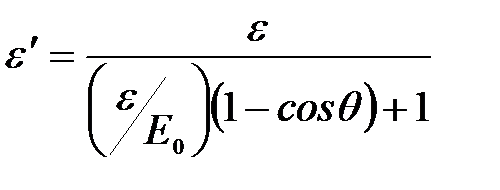 .
.
Откуда: 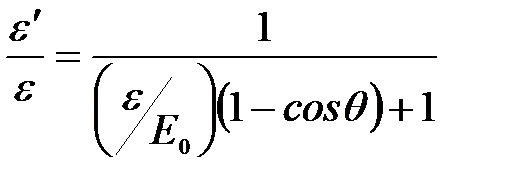 .
.
Следовательно, 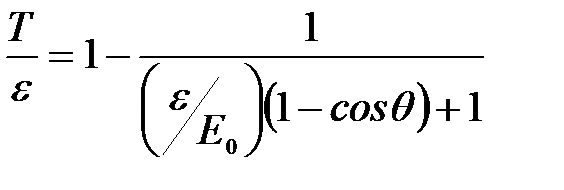 .
.
Произведём вычисления: 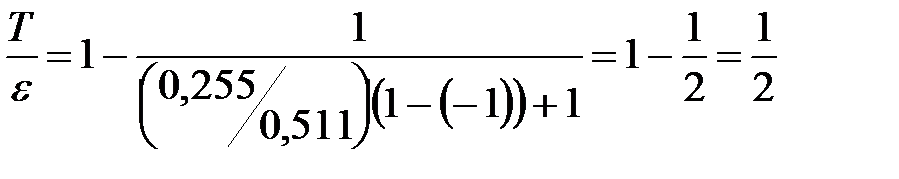 .
.
Ответ: 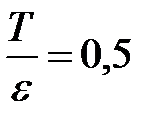 .
.
Задачи для самостоятельного решения
1. При освещении катода вакуумного фотоэлемента монохроматическим светом с длиной волны 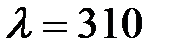 нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25%, задерживающее напряжение оказывается меньше на 0,8В. Определить по этим экспериментальным данным постоянную Планка.
нм фототок прекращается при некотором задерживающем напряжении. При увеличении длины волны на 25%, задерживающее напряжение оказывается меньше на 0,8В. Определить по этим экспериментальным данным постоянную Планка.
2. Плоский серебряный электрод освещается монохроматическим излучением с длиной волны 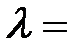 83 нм. Определить, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряжённостью Е = 10 В/см? «Красная граница» фотоэффекта для серебра
83 нм. Определить, на какое максимальное расстояние от поверхности электрода может удалиться фотоэлектрон, если вне электрода имеется задерживающее электрическое поле напряжённостью Е = 10 В/см? «Красная граница» фотоэффекта для серебра 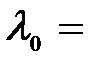 264 нм.
264 нм.
3. При освещении вакуумного фотоэлемента монохроматическим светом с длиной волны 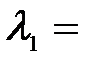 0,4 мкм он заряжается до разности потенциалов φ1 = 2 В. Определить, до какой разности потенциалов зарядится фотоэлемент при освещении его монохроматическим светом с длиной волны
0,4 мкм он заряжается до разности потенциалов φ1 = 2 В. Определить, до какой разности потенциалов зарядится фотоэлемент при освещении его монохроматическим светом с длиной волны 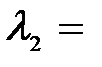 0,3 мкм?
0,3 мкм?
4. Выбиваемые светом при фотоэффекте электроны при облучении фотокатода видимым светом полностью задерживаются обратным напряжением 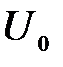 = 1,2 В. Специальные измерения показали, что длина волны падающего света
= 1,2 В. Специальные измерения показали, что длина волны падающего света 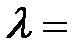 400 нм. Определить «красную границу» фотоэффекта.
400 нм. Определить «красную границу» фотоэффекта.
5. На цинковую пластину падает монохроматический свет с длиной волны 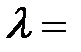 220 нм. Определить максимальную скорость
220 нм. Определить максимальную скорость 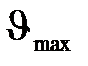 фотоэлектронов.
фотоэлектронов.
6. Определить длину волны l ультрафиолетового излучения, падающего на поверхность некоторого металла, при максимальной скорости фотоэлектронов равной 10 Мм/с. Работой выхода электронов из металла пренебречь.
7. Фотон ( 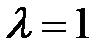 пм) рассеялся на свободном электроне под углом
пм) рассеялся на свободном электроне под углом 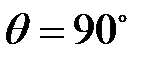 . Какую долю своей энергии фотон передал электрону?
. Какую долю своей энергии фотон передал электрону?
8. При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния 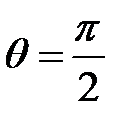 . Найти энергию (
. Найти энергию ( 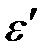 ) и импульс (
) и импульс ( 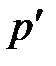 ) рассеянного фотона.
) рассеянного фотона.
9. Энергия 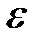 падающего фотона равна энергии покоя электрона. Определить долю
падающего фотона равна энергии покоя электрона. Определить долю 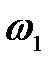 энергии падающего фотона, которую сохранит рассеянный фотон, и долю
энергии падающего фотона, которую сохранит рассеянный фотон, и долю 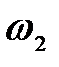 этой энергии, полученную электроном отдачи, если угол рассеяния
этой энергии, полученную электроном отдачи, если угол рассеяния 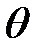 равен: 1) 60°; 2) 90°; 3) 180°.
равен: 1) 60°; 2) 90°; 3) 180°.
10. Определить, с какой скоростью должен двигаться электрон, чтобы его импульс ре был равен импульсу фотона рγ, длина волны которого l = 2 пм?
Практическое занятие 4
Тема: «Планетарная модель атома. Строение атома водорода по Бору. Спектры излучения атомов»
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Планетарная модель атома. Строение атома водорода по Бору. Спектры излучения атомов»
2. Привитие навыков решения задач по данной теме.
Краткая теория
В 19 веке впервые были открыты явления, обнаруживающие сложность строения и свойств атомов, которые до этого рассматривались как мельчайшие частицы вещества. Так в 1833 году М. Фарадей установил, что ток в растворе электролита – это упорядоченное движение заряженных частиц (ионов), минимальный заряд которых примерно равный е = 1,60∙10-19 Кл был назван элементарным электрическим зарядом. В 1896 году французский ученый Беккерель обнаружил явление естественной радиоактивности солей урана. Это явление исследовали Пьер и Мария Кюри, доказав, что из атомов вылетают и электроны, и положительно заряженные частицы (впоследствии названные α-частицами). На сложную структуру атомов указывали спектроскопические исследования, которые привели к открытию линейчатых спектров атомов. В начале XIX века были открыты дискретные спектральные линии в излучении атомов водорода в видимой части спектра, и впоследствии были установлены математические закономерности, связывающие длины волн этих линий (И. Бальмер, 1885 г.). В 1897 году Дж. Томсон открыл электрон и измерил отношение e/m заряда электрона к массе. Опыты Томсона подтвердили вывод о том, что электроны входят в состав атомов, причем носителями отрицательного заряда атомов являются легкие электроны, масса которых составляет лишь малую долю массы атомов. Основная часть массы атомов связана с положительным зарядом.
В первой модели атома Дж. Томсона (1903 г.) атом рассматривался как заполненный положительным электричеством шар, внутри которого находились электроны. Атом в целом был электронейтрален. Однако в дальнейшем выяснилась несостоятельность этой модели.
В начале ХХ века английский физик Э. Резерфорд, анализируя данные по рассеянию 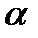 -частиц тонкими металлическими образцами, выдвинул так называемую «планетарную» модель строения атома.
-частиц тонкими металлическими образцами, выдвинул так называемую «планетарную» модель строения атома.
Рассеяние α-частиц при прохождении через фольгу вызывается кулоновскими силами, т.е. электрическим взаимодействием частицы и заряда атома. Гравитационное взаимодействие в 1033 раз меньше, поэтому фактически роли не играет.
Какие же заряды в атоме вызывают рассеяние α-частиц? Электроны не могут этого сделать, так как их масса много меньше массы частицы: ma=7350me. При взаимодействии с электронами быстро движущаяся частица не изменяет направление своего движения.
|
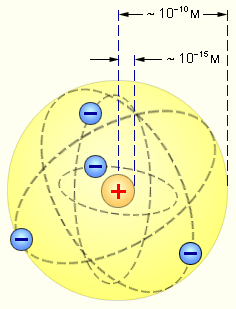
| Рис. 4.1. Планетарная модель атома |
Причиной рассеяния a-частиц является их взаимодействие с положительно заряженными частицами атома, занимающими очень малую область атома. Резерфорд назвал эту область ядром. В ядре сосредоточена почти вся масса атома и весь положительный заряд. Обобщив результаты опытов, Резерфорд предложил следующую модель строения атома, в рамках которой предполагается, что в центре атома находится тяжелое положительно заряженное ядро, вокруг которого, подобно планетам вокруг Солнца, вращаются легкие отрицательно заряженные электроны. Атомы имеют размеры порядка 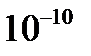 м, а ядра – порядка
м, а ядра – порядка 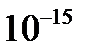 м, т.е. атом на 99.9% пустой (рис.4.1). Практически вся масса атома сосредоточена в ядре, поэтому ядерная материя обладает огромной плотностью:
м, т.е. атом на 99.9% пустой (рис.4.1). Практически вся масса атома сосредоточена в ядре, поэтому ядерная материя обладает огромной плотностью: 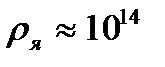 г/cм3.
г/cм3.
Однако планетарная модель атома является внутренне противоречивой. Движущийся с ускорением заряд излучает электромагнитную волну. При этом энергия атома уменьшается: электрон должен упасть на ядро, а атом прекратить свое существование.
На самом деле атомы химических элементов представляют собой устойчивые структуры, существующие десятки тысяч лет без изменения. Поэтому модель атома Резерфорда была дополнена рядом положений, автором которых является датский физик Бор.
В 1913 году Бор показал, что несовпадение с экспериментом выводов, основанных на модели Резерфорда, возникло потому, что поведение микрочастиц нельзя описывать теми же законами, что и макроскопических тел.
Бор предположил, что величины характеризующие микромир, должны квантоваться, т.е. они могут принимать только определенные дискретные значения.
Законы микромира - квантовые законы. Эти законы в начале 20 столетия еще не были установлены наукой. Бор сформулировал их в виде трех постулатов, дополняющих ( и "спасающих") атом Резерфорда.
Первый постулат (постулат стационарных состояний) :
Атомы имеют ряд стационарных состояний соответствующих определенным значениям энергий: Е1, Е2...En. Находясь в стационарном состоянии, атом энергии не излучает и не поглощает энергию, несмотря на движение электронов. Энергии стационарных состояний образуют дискретный спектр.
Второй постулат (правило квантования орбит):
В стационарном состоянии атома электроны движутся по стационарным орбитам, для которых выполняется квантовое соотношение:
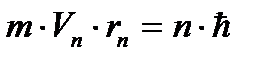 (4.1)
(4.1)
где m - масса электрона, rn- радиус орбиты с номером n (n=1,2,3...), 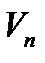 - скорость электрона на этой орбите, ħ - постоянная Планка.
- скорость электрона на этой орбите, ħ - постоянная Планка.
Третий постулат (правило частот):
Излучение или поглощение энергии атомом происходит при переходе его из одного стационарного состояния в другое. При этом излучается или поглощается порция энергии (квант), равная разности энергий стационарных состояний, между которыми происходит переход:
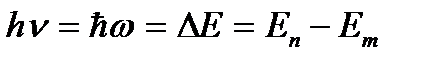 (4.2)
(4.2)
Постулаты Бора противоречат законам классической физики. Они выражают характерную особенность микромира - квантовый характер происходящих там явлений. Выводы, основанные на постулатах Бора, хорошо согласуются с экспериментом. Например, объясняют закономерности в спектре атома водорода, происхождение характеристических спектров рентгеновских лучей и т.д. На рис. 4.2 показана часть энергетической диаграммы стационарных состояний атома водорода.
Планетарная модель продемонстрировала прекрасное согласие с экспериментом при описании атома водорода, однако для описания свойств многоэлектронных атомов она оказалась не пригодна. Основной недостаток этой модели заключается в отсутствии учета взаимодействия электронов между собой.
Постулаты Бора нашли своё экспериментальное подтверждение в опытах Д.Франка и Г.Герца (1913), в которых изучались столкновения электронов с атомами газов.
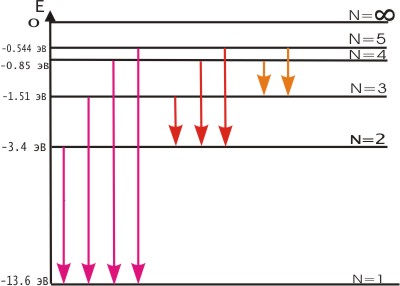
Рис. 4.2. Энергетическая диаграмма стационарных состояний атома водорода
Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем - систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не+, Li2+), а также теоретически вычислить постоянную Ридберга. 
Выражение для радиуса n-й стационарной орбиты:
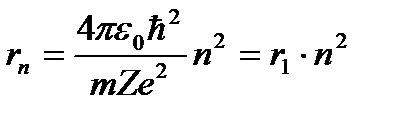 , ( n = 1, 2, 3, …). (4.3)
, ( n = 1, 2, 3, …). (4.3)
Для атома водорода (Z = 1) радиус первой орбиты электрона при n = 1, называемый первым боровским радиусом (rB), равен
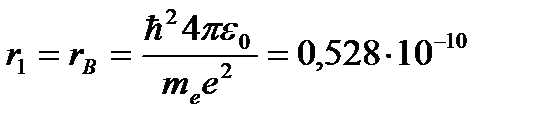 (4.4)
(4.4)
Полная энергия электрона в водородоподобной системе складывается из его кинетической энергии 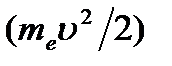 и потенциальной энергии в электростатическом поле ядра
и потенциальной энергии в электростатическом поле ядра 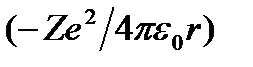 :
:
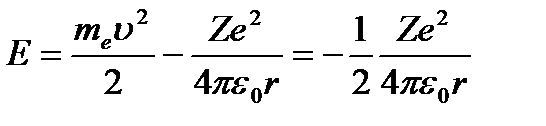 (4.5)
(4.5)
Учитывая квантованные для радиуса n-й стационарной орбиты значения (4.4), получим, что энергия электрона может принимать только следующие дозволенные дискретные значения:
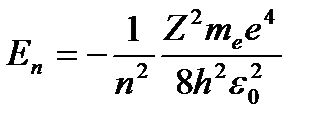 (n = 1, 2, 3, …), (4.6)
(n = 1, 2, 3, …), (4.6)
где m - масса электрона, e = 1.610-19 Кл - и заряд электрона; 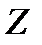 – порядковый номер элемента в таблице Менделеева. Знак « - » означает, что электрон находится в связанном состоянии.
– порядковый номер элемента в таблице Менделеева. Знак « - » означает, что электрон находится в связанном состоянии.
Из формулы (4.6) следует, что энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения n. Целое число n в выражении (3.6), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n = 1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.
Придавая n различные целочисленные значения, получим для атома водорода (Z = 1) возможные уровни энергии, схематически представленные на рис.4.2 и 4.3. На рис.4.2 изображена диаграмма энергетических уровней атома водорода и указаны переходы, соответствующие различным спектральным сериям. Рис.4.3 иллюстрирует образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.
Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n = ∞. Атом водорода обладает, таким образом, минимальной энергией (Е1=-13,6 эВ) при п = 1 и максимальной (Е∞ = 0) при n = ∞. Следовательно, значение Е∞ = 0 соответствует ионизации атома (отрыву от него электрона). Согласно третьму постулату Бора, при переходе атома водорода ( Z = 1) из стационарного состояния n в стационарное состояние т с меньшей энергией испускается квант
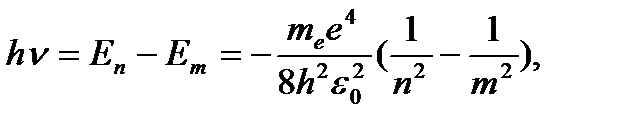 (4.7)
(4.7)
Откуда частота излучения
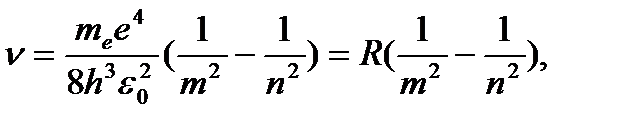 (4.8)
(4.8)
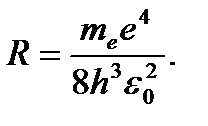 (4.9)
(4.9)
R – постоянная Ридберга.
Прекрасное согласие боровской теории атома водорода с экспериментом служило веским аргументом в пользу ее справедливости. Стало ясно, что атомы – это квантовые системы. Энергетические уровни стационарных состояний атомов дискретны.
Однако попытки применить теорию Бора к более сложным атомам (даже для атома гелия) не увенчались успехом. Эта теория обладает внутренними противоречиями: с одной стороны, применяет законы классической физики, а с другой - основывается на квантовых постулатах. Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано де Бройлем (1923) на основе представлений о волновых свойствах частиц.
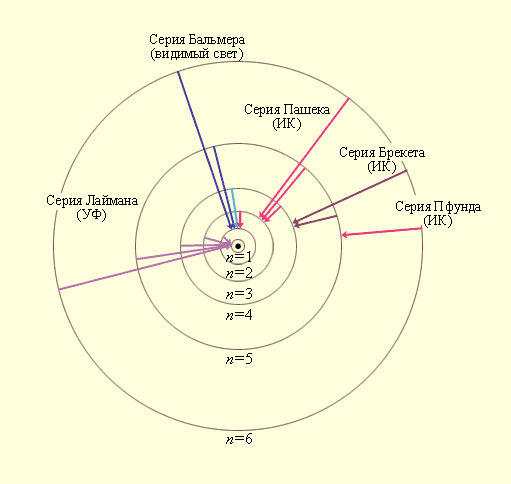
Рис.4.3. Стационарные орбиты атома водорода и образование
спектральных серий.
Примеры решения задач
Задача 1. Определить потенциальную П, кинетическую Т и полную Е энергии электрона, находящегося на первой орбите атома водорода (основное состояние).
| Дано: Z = 1 n = 1 mе = 9,11·10-31 кг е = 1,6·10-19 Кл h = 6,626·10-34 Дж·с ε0 = 8,85·10-12 Ф/м |
| 1) П = ? 2) Т = ? 3) Е = ? |
Решение:
Потенциальная энергия электрона в электростатическом поле ядра и радиус орбиты rn электрона:
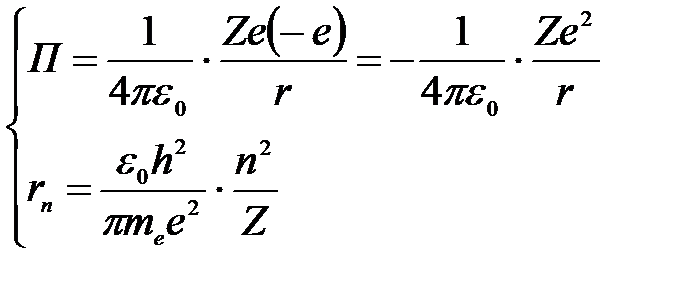 .
.
Тогда потенциальная энергия электрона на любой орбите водородоподобного атома (считаем энергию электрона в бесконечности равной нулю):
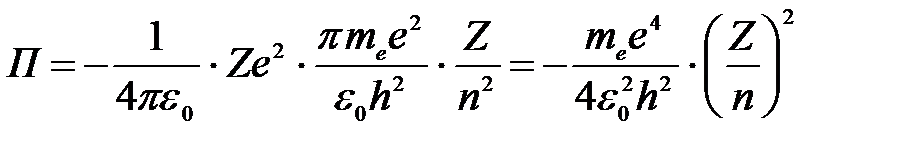 . .
|
Потенциальная энергия для основного состояния атома водорода Z = 1, n = 1:
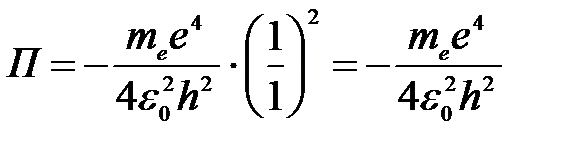 .
.
Вычислим:
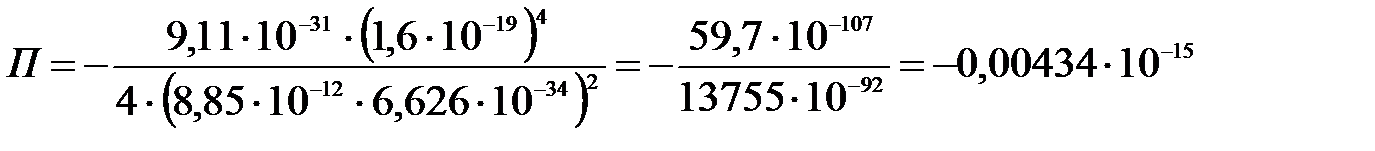 ;
;
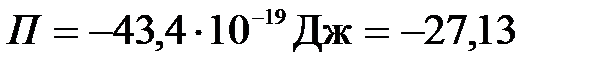 эВ.
эВ.
2) Кинетическая энергия электрона при движении по окружности и скорость электрона на этой орбите :
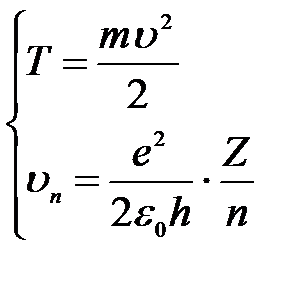 .
.
Тогда кинетическая энергия электрона на любой орбите водородоподобного атома:
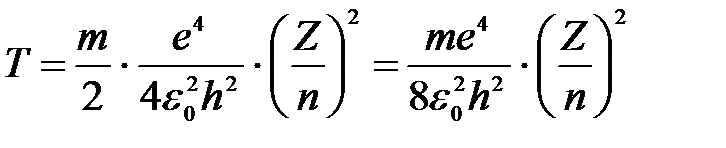 . .
|
Кинетическая энергия для основного состояния атома водорода Z=1, n=1:
 .
.
Вычислим:
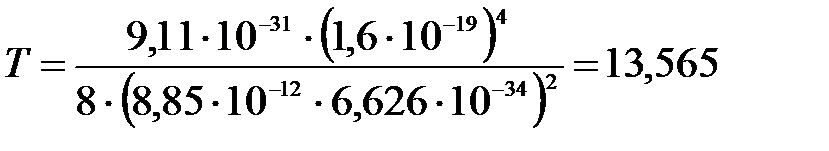 эВ.
эВ.
3) Полная энергия электрона на любой орбите водородоподобного атома:
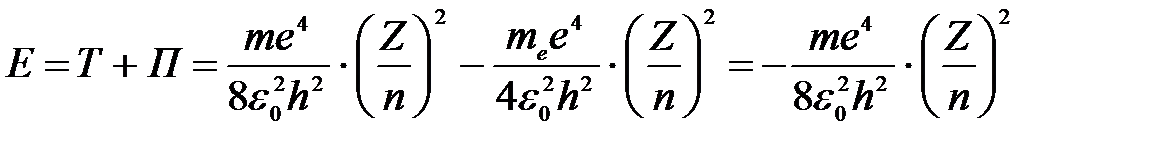 . .
| (3) |
Полная энергия для основного состояния атома водорода Z = 1, n = 1:
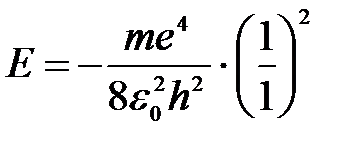 .
.
Вычислим:
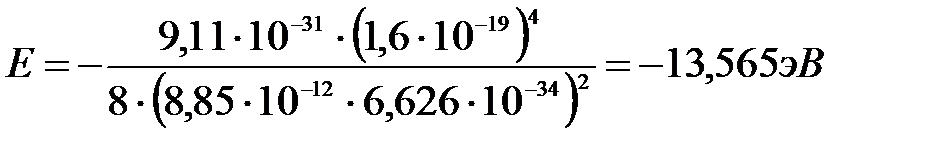 .
.
Задача 2. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.
| Дано: Z = 1 m = 2 n = 3 h=6,626·10-34 Дж·с с = 3·108 м/с R = 3,29 1015 c-1 R/ = 1,097 107 м-1 Е i = 13,6 эВ mе = 9,11·10-31 кг е = 1,6·10-19 Кл |
| ε3,2 =? |
Решение:
Способ 1. Энергия фотона:
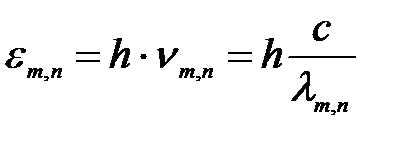 , (1)
, (1)
где h – постоянная Планка, с – скорость света в вакууме, ν – частота излучения, λ – длина волны излучения m, n – стационарные орбиты; m = 1, 2, 3, 4, 5, 6 (определяет серию), n = m + 1, m + 2, m + 3…(определяет отдельные линии этой серии), n = ∞ определяет границу серии.
Обобщённая формула Бальмера (сериальная формула):
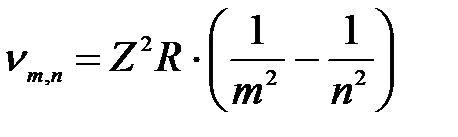 (2)
(2)
или 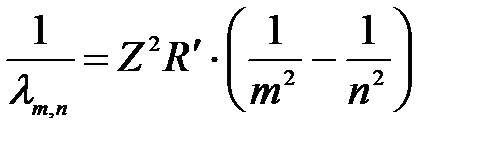 , (2-а) , (2-а)
|
где R = R/с = 3,28805∙1015 1/с – постоянная Ридберга,
R/ = 1,097373177∙107 м-1 – штриховая постоянная Ридберга,
Z – зарядовое число (порядковый номер в таблице Менделеева).
Подставим формулу (2) частоты в (1):
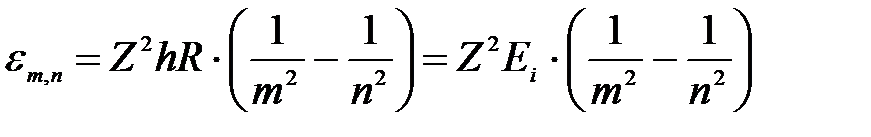 , ,
| (3а) |
или через длину волны:
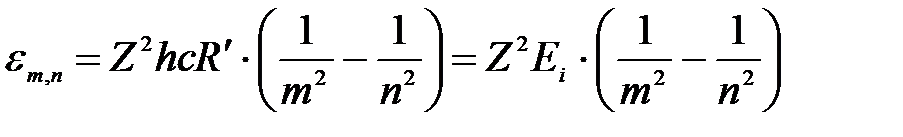 , ,
| (3б) |
где Е i – энергия ионизации водорода. Получили одинаковую формулу.
Произведем вычисления во внесистемных единицах:
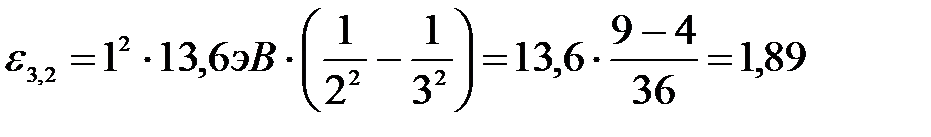 (эВ).
(эВ).
Способ 2. Второй постулат Бора (правило частот):
| εn,m = ΔЕ = Еn – Em = Eдо – Eпосле, | (4) |
где ε n,m – энергия испускаемого (поглощаемого) атомом фотона при переходе атома из одного стационарного состояния в другое; Еn и Em – энергии стационарных состояний, характеризуемые квантовыми числами n и m, определяемые по формуле:
 , ,
| (5) |
где е – элементарный заряд, ε0 – электрическая постоянная, Z – атомный номер (зарядовое число, порядковый номер атома в таблице Д.И. Менделеева).
При Em < En происходит излучение фотона, при Em > En – его поглощение.
Тогда энергия испускаемого фотона:
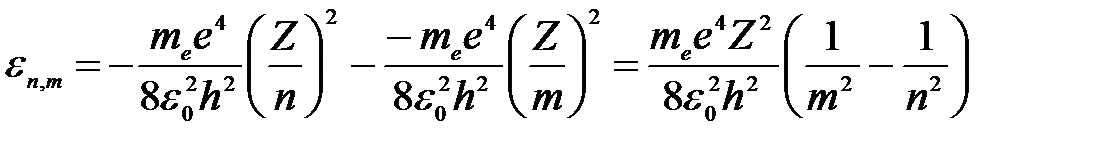 .
.
Подставим числа:
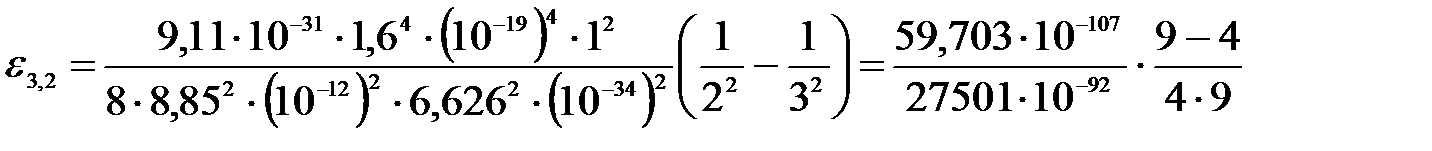 ;
;
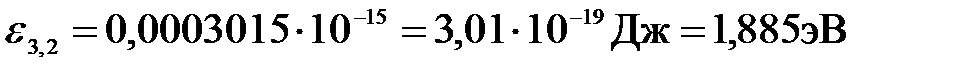 .
.
Ответ: ε3,2 = 1,89 эВ, относится к серии Бальмера.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| орбита |
| e |
| Рис. 4.4 |
Задача 3. Определить длину волны спектральной линии, соответствующую переходу электрона в атоме водорода с шестой боровской орбиты на вторую (рис.4.4) К какой серии относится эта линия? Которая она по счёту?
Дано:
m = 2
n = 6
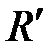 = 1,097 107 м-1 = 1,097 107 м-1
|
| l =? |
Решение:
Запишем обобщенную формулу Бальмера:
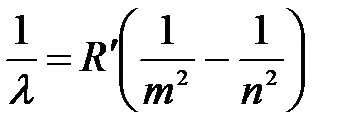 ,
,
где l – длина волны спектральных линий в спектре атома Бора; m – определяет серию; n – определяет отдельные линии этой серии (m < n); 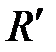 – штриховая постоянная Ридберга.
– штриховая постоянная Ридберга.
Отсюда длина волны:
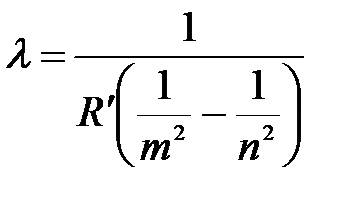 .
.
Произведем вычисления:
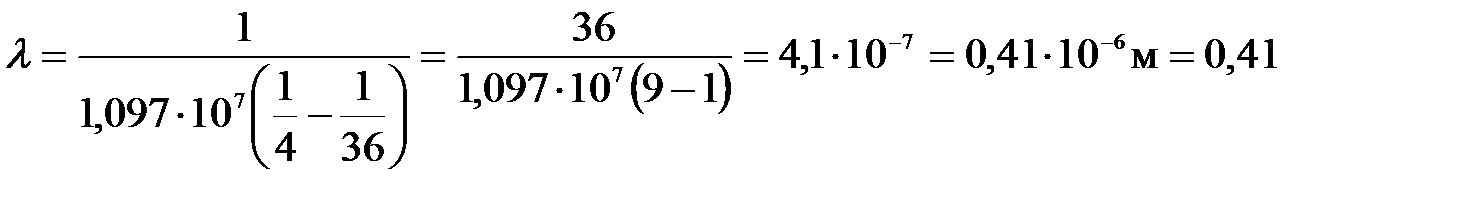 мкм.
мкм.
Это – серия Бальмера, т.к. m = 2. По счёту она 4я, т.к. n – m = 6 – 2 =4.
Ответ: l = 0,41 мкм, серия Бальмера, по счёту № 4.
Задача 4. Насколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны l = 486 нм?
| Дано: Z = 1 l = 486 нм | СИ: 486∙10-9 м |
| DЕк -? |
Решение:
Из закона сохранения энергии: разность полных энергий электрона соответствующих орбит равна энергии излучения:
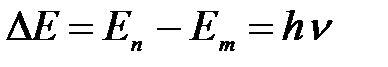 .
.
Частота это есть отношение скорости света к длине волны:
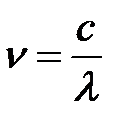 .
.
Полная энергия электрона по модулю равна кинетической энергии:
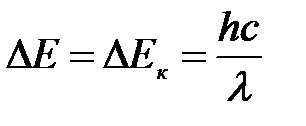 .
.
Подставим численные значения:
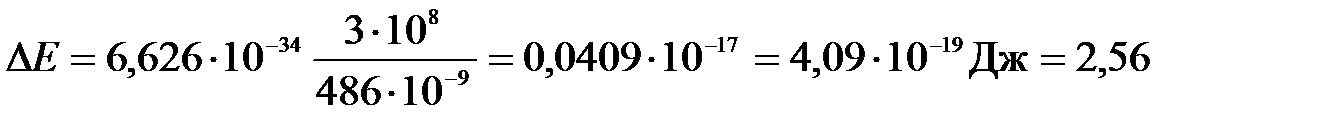 (эВ).
(эВ).
Ответ: DЕк = 2,56 эВ.
Задачи для самостоятельного решения
1. Рассмотрите стационарное состояние атома водорода с n = 50 в рамках боровской модели. Вычислите: а) энергию связи электрона в эВ; б) радиус орбиты электрона; в) частоту обращения электрона на орбите; г) длину волны излучения, испущенного при переходе между стационарными состояниями с n =50 и n = 49 .
2. Спутник с массой 10 кг обращается вокруг Земли за 2 часа по орбите радиусом 8000 км. а) Считая, что постулат Бора о моменте количества движения применим к спутнику в той же мере, как и к электрону атома водорода, определите квантовые числа орбиты спутника; б) покажите, исходя из первого постулата Бора и закона тяготения Ньютона, что радиус орбиты спутника прямо пропорционален квадрату квантового числа: r = kn2, где k – коэффициент пропорциональности; в) используя результат (б), определите расстояние между орбитой спутника, данной в условии задачи и следующей «разрешенной» орбитой; г) подумайте над возможностью наблюдения разделения двух соседних орбит; д) совпадают ли квантовая и классическая орбиты спутника? Какой из методов вычисления орбит «правильный»?
3. В каких пределах должна быть энергия бомбардирующих электронов, чтобы при возбуждении атома водорода ударами этих электронов спектр излучения водорода имел лишь одну спектральную линию? Энергия атома водорода в основном состоянии E1 = – 13,6 эВ.
4. Найдите скорость электронов, вырываемых электромагнитным излучением с длиной волны 18 нм из иона Не+, находящегося в основном состоянии. Энергия ионизации атома водорода 13,6 эВ.
5. Вычислить радиус второй орбиты r2 электрона в ионе гелия He+.
6. Вычислить скорость υ4 электрона на четвёртой орбите для иона лития Li++.
7. Найти энергию Е i и потенциал Ui ионизации иона He+.
8. Найти первую энергию возбуждения Е1 и первый потенциал возбуждения U1 иона Li++.
9. Определить длину волны l, соответствующую второй спектральной линии в серии Пашена.
10. Определить максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера).
Практическое занятие 5
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Корпускулярно-волновой дуализм свойств вещества. Волны де Бройля. Соотношение неопределенностей».
2. Привитие навыков решения задач по данной теме.
Краткая теория
Примеры решения задач
Задача 1. Электрон прошел ускоряющую разность потенциалов 51 В. Найти длину волны де Бройля для электрона.
| Дано: U = 51 В |
| l Б - ? |
Решение:
Запишем формулу де Бройля:
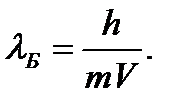
Пройдя ускоряющую разность потенциалов, электрон приобрел кинетическую энергию (нерелятивистский случай):
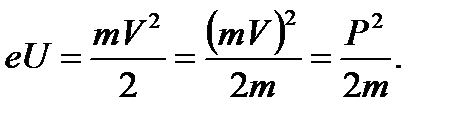
Отсюда выразим импульс электрона и запишем выражение для длины волны де Бройля:
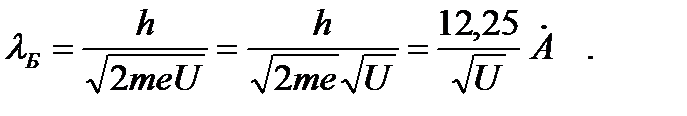
Вычислим длину волны де Бройля:
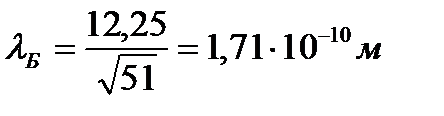
Ответ: λБ = 1,71 Å
Задача 2. Вычислите дебройлевские длины волн электрона, протона и атома урана, имеющих одинаковую кинетическую энергию 100 эВ.
| Дано: Wk = 100 эВ | СИ: 1.6 × 10-17 Дж |
| l Б - ? |
Решение
Кинетическая энергия нерелятивистских частиц определяется выражением
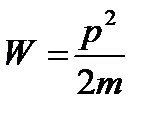 .
.
Откуда 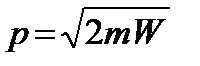 .
.
Дебройлевская длина волны электрона
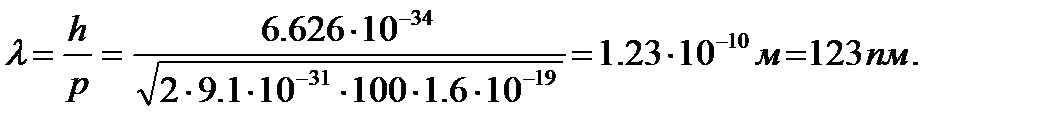
Дебройлевская длина волны протона
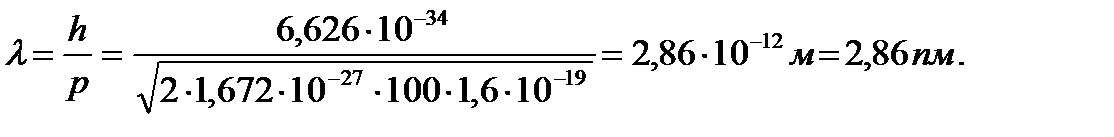
Дебройлевская длина волны атома урана:
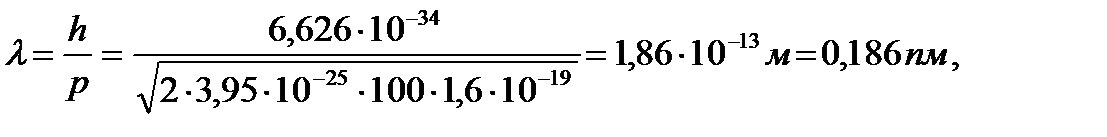
где масса атома урана
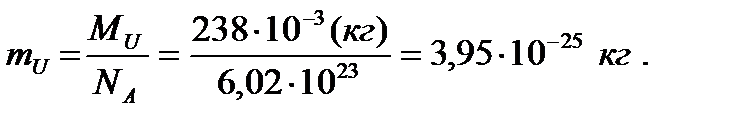
Задача 3. Кинетическая энергия электрона в атоме (К) составляет величину 10 эВ. Оценить минимальные размеры атома, используя соотношение неопределенностей.
| Дано: К = 10 эВ me = 9.11 × 10-31 кг | СИ: 1.6 × 10-18 Дж |
| lmin - ? |
Решение
Электрон находится в атоме, линейные размеры которого l. Следовательно, неопределенность координаты равна:
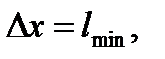
Запишем соотношение неопределенностей, подставив величину Δх:
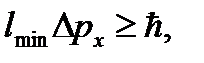
где 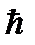 = 1.054 × 10-34 Дж × с – постоянная Планка.
= 1.054 × 10-34 Дж × с – постоянная Планка.
Поскольку надо найти минимальные размеры атома, то Dpx не должно превышать px, т.е. Dpx = px. Импульс связан с кинетической энергией электрона соотношением:
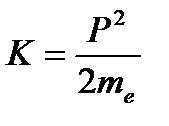
Из последнего уравнения выразим импульс электрона, подставим его в соотношение неопределенностей и решим полученное уравнение относительно минимально линейного размера атома:
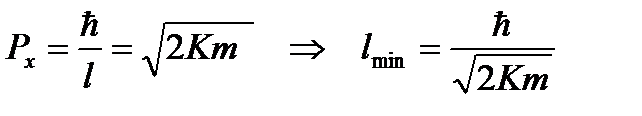
Подставив числовые значения, рассчитаем минимальный размер атома:
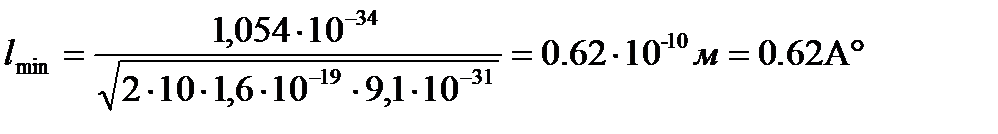
Ответ: lmin = 0.62 Å.
Задача 4. Атом излучает фотон с длиной волны 550 нм. Время излучения 10-8 с. Определить неточность в определении указанной длины волны и с какой точностью может быть определено местонахождение данного фотона в направлении его движения.
| Дано: l = 550 нм D t = 10-8 с c = 3 × 108 м/ c | СИ 5.5 × 10-7 м |
| D l - ? D x - ? |
Решение
Запишем уравнение для расчета энергии кванта (фотона):
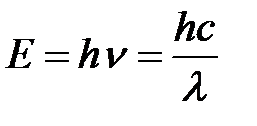

Для нахождения неточности в определении указанной длины волны (Δλ) возьмем производную от энергии по длине волны и выразим неточность в определении энергии кванта ΔЕ:
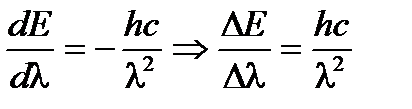
Запишем соотношение неопределенностей для энергии и выразим из него неточность в определении энергии излученного кванта (фотона) ΔЕ:
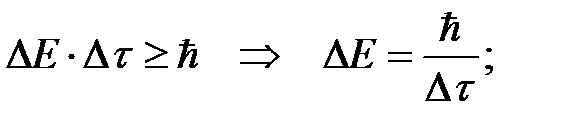
Приравняем выражения для величины ΔЕ, полученные выше. Решим последнее уравнение относительно искомой величины Δλ:
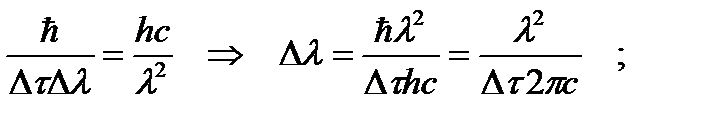
Запишем уравнение де Бройля относительно импульса фотона. Возьмем производную от импульса по λ и выразим неточность в определении его импульса ΔР:
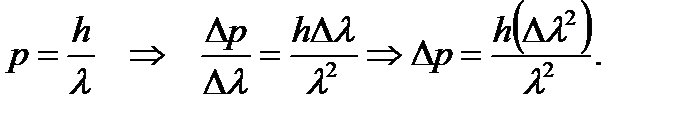
Используем соотношение неопределенностей для расчета величины неточности в определении координаты фотона ΔХ:
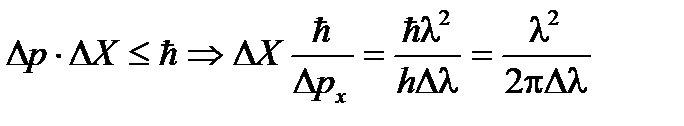
Произведем вычисления заданных величин:
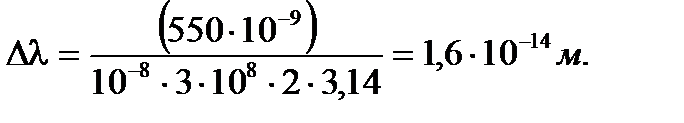
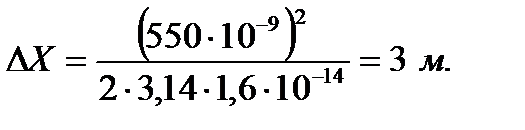
Ответ: 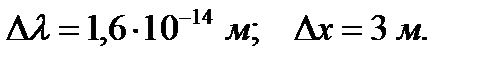
Задачи для самостоятельного решения
1. Электрон движется по окружности радиусом R = 0,5 см в однородном магнитном поле с индукцией В = 8 мТл. Определить длину его волны де Бройля.
2. Определить длину волны де Бройля для нейтрона, движущегося со наиболее вероятной скоростью при комнатной температуре.
3. Найти длину волны де Бройля lБ для электрона, движущегося по круговой орбите атома водорода, находящегося в основном состоянии.
4. Найти длину волны де Бройля 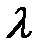 для атома водорода, движущегося при температуре
для атома водорода, движущегося при температуре 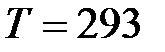 К со: 1) средней квадратичной скоростью; 2) наиболее вероятной скоростью; 3) средней арифметической скоростью.
К со: 1) средней квадратичной скоростью; 2) наиболее вероятной скоростью; 3) средней арифметической скоростью.
5. Найти длину волны де Бройля λ протона, прошедшего ускоряющую разность потенциалов U: 1) 1кВ; 2) 1ГВ.
6. Время жизни атома в возбужденном состоянии t=10 нс. Учитывая, что постоянная Планка ћ = 6,6×10-16 эВ×с, определите ширину энергетического уровня (в эB).
7. Среднее время жизни возбуждённого состояния атома равно τ = 12 нс. Определите минимальную неопределённость длины волны Δλ = 0,12 мкм излучения при переходе атома в основное состояние.
8. Оцените наименьшие ошибки, с которыми можно определить скорость шарика массой 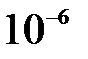 кг и электрона, если положение центра шарика и положение электрона установлены с точностью
кг и электрона, если положение центра шарика и положение электрона установлены с точностью 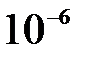 м. Постоянная Планка
м. Постоянная Планка 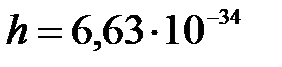 Дж·с.
Дж·с.
9. Определить неопределенность в определении координаты электрона, движущегося в атоме водорода со скоростью v=1,5 Мм/с, если допускаемая неопределенность скорости составляет 10% от её величины. Сравнить полученный результат с диаметром атома водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.
10. Используя соотношение неопределённостей энергии и времени, определить естественную ширину спектральной линии излучения атома при переходе его из возбуждённого состояния в основное. Среднее время жизни атома в возбуждённом состоянии принять равным 10нс, а длину волны излучения - равной 600 нм.
Практические занятия 6-7
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Волновая функция. Уравнение Шредингера. Движение заряженных частиц в потенциальной «яме» с бесконечно высокими «стенками». Туннельный эффект».
2. Привитие навыков решения задач по данной теме.
Краткая теория
Уравнение Шредингера
В классической физике второй закон Ньютона позволяет решать основную задачу – по заданным силам, действующим на тело, и по начальным условиям определить в любой момент времени координаты тела, его скорость, т.е., описать движение тела в пространстве и во времени. В квантовой механике необходимо учесть двойственную природу микрочастиц, которая ограничивает возможность применения к таким частицам классических понятий о координате и скорости. Это уравнение должно быть таким, чтобы позволяло учесть волновые свойства частиц. Поскольку положение частицы в пространстве задается в квантовой механике через волновую функцию y (x , y . z . t), то основное уравнение квантовой механики должно быть уравнением относительно функции y (x,y.z.t). Это уравнение должно быть волновым, ибо из него должны получить свое объяснение опыты по дифракции микрочастиц.
Основное уравнение квантовой механики было найдено в 1926 году Э.Шредингером. Как и законы Ньютоны, уравнение Шредингера не выводится, а постулируется. Справедливость данного уравнения подтверждается тем, что выводы квантовой механики, полученные с его помощью в атомной и ядерной физике, находятся в хорошем согласии с опытом. Уравнение Шредингера имеет вид:
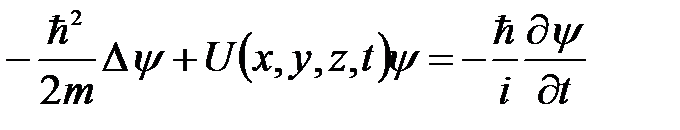 , (6.7)
, (6.7)
где m – масса частицы; U ( x , y , z , t ) – потенциальная энергия частицы в силовом поле, где она движется; 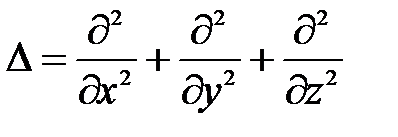 - оператор Лапласа, y = y ( x , y , z , t ) - искомая волновая функция.
- оператор Лапласа, y = y ( x , y , z , t ) - искомая волновая функция.
Уравнение (6.7) называют временным или общим уравнением Шредингера. Оно справедливо для любой частицы с массой m, которая движется со скоростью V << c. Решение уравнения (6.7) можно представить в виде:
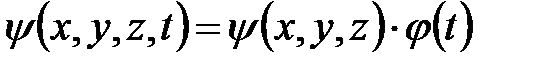 , (6.8)
, (6.8)
где y (x,y,z) - координатная или амплитудная часть волновой функции; j ( t ) - временная часть волновой функции.
При решении ряда физических задач микромира необходимо уметь находить стационарные, т.е., не содержащие времени, решения уравнения Шредингера. Это имеет смысл в тех случаях, когда потенциальная энергия частицы не зависит от времени U = U ( x , y , z ). Решением в этом случае будет волновая функция вида y =y(x, y, z), т.е. ее амплитудная часть. Уравнение Шредингера, соответствующее этому решению, принимает вид
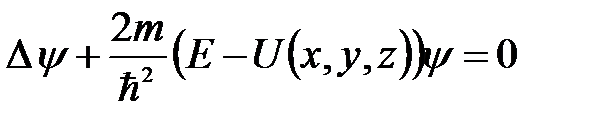 , (6.9)
, (6.9)
где m – масса частицы; Е –полная энергия частицы; D - оператор Лапласа.
Это уравнение называется стационарным уравнением Шредингера.
Волновые функции y =y(x,y,z,t), удовлетворяющие уравнению Шредингера при данном U = U ( x , y , z ), называют собственными функциями. Значения полной энергии (Е), при которых существуют решения уравнения Шредингера (6.9), называются собственными значениями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае будет присутствовать сплошной спектр энергий, а во втором – дискретный.
Движение свободной частицы
Свободная частица – это частица, движущаяся в отсутствие внешних полей. Рассмотрим частицу, которая движется вдоль оси Ох, то есть, будем решать одномерную задачу. Поскольку частица свободная, на нее не действуют силы и ее потенциальная энергия U ( x ) = const. Положим U ( x ) равной нулю. Тогда полная энергия этой частицы совпадает с кинетической и стационарное уравнение Шредингера (6.9) принимает вид:
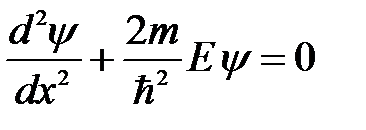 ; (6.10)
; (6.10)
если ввести обозначение
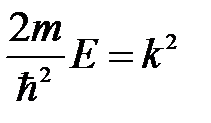 , (6.11)
, (6.11)
то уравнение (6.10) можно записать в виде:
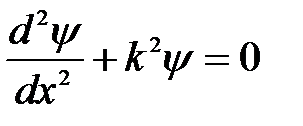 . (6.12)
. (6.12)
Решение уравнения (6.12) имеет вид
y ( x ) = A × eikx, (6.13)
где A = const и k = с onst .
Собственные значения энергии получим из (6.11):
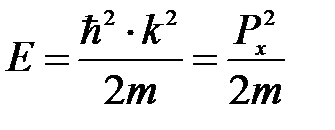 . (6.14)
. (6.14)
Зависимость энергии от импульса частицы имеет вид, типичный для нерелятивистской частицы. Следовательно, энергия свободной частицы (Е), как и волновое число (k), может принимать любые значения, т.е., ее энергетический спектр является непрерывным. Таким образом, свободная микрочастица описывается плоской монохроматической волной де Бройля. Этому соответствует плотность вероятности обнаружения частицы в данной точке пространства, которая не зависит от времени:
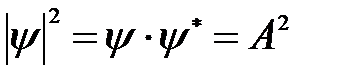 , (6.15)
, (6.15)
т.е. все положения частицы в пространстве равновероятны.
Туннельный эффект
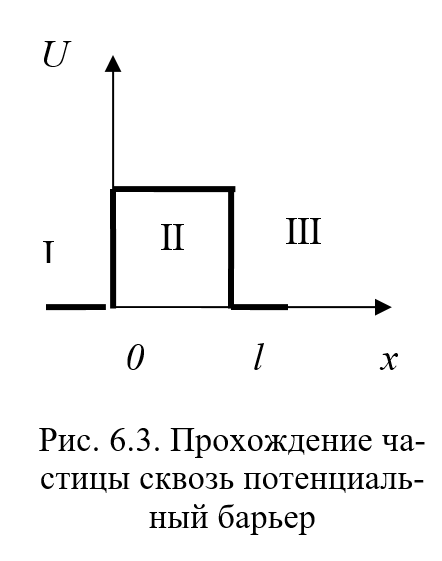 Качественное различие свойств макро- и микрочастиц особенно резко сказывается в их поведении при встрече с потенциальным барьером. Предположим, частица движется вдоль оси Ох в таком силовом поле, когда область движения частицы разделена потенциальным барьером.
Качественное различие свойств макро- и микрочастиц особенно резко сказывается в их поведении при встрече с потенциальным барьером. Предположим, частица движется вдоль оси Ох в таком силовом поле, когда область движения частицы разделена потенциальным барьером.
U ( x ) = 0 при x < 0 и x > l ,
U ( x ) = const при 0 < x < l .
Если полная энергия частицы E < U, то с классической точки зрения частица может двигаться лишь в областях I и III ( x < 0 или x > l ). Проникнуть в область барьера она не может, так как там ее кинетическая энергия, равная E к = E – U , оказалась бы отрицательной, что невозможно. Такая частица не может перейти из области I в область III. По-иному проявляет себя микрочастица, поведение которой описывается уравнением Шредингера. Волновая функция в этом случае будет отлична от нуля и в области II, благодаря чему вероятность ее проникновения из области I в область III окажется отличной от нуля. Следовательно, микрочастица с энергией, меньшей, чем высота барьера, способна пройти («просочиться») сквозь потенциальный барьер. Это явление называется туннельным эффектом, для его описания вводится коэффициент прозрачности D потенциального барьера. Если, по аналогии с оптикой, для волн де Бройля подсчитать интенсивность падающей на барьер волны (I пад) и интенсивность волны, прошедшей сквозь барьер (I прох), то прозрачностью, или коэффициентом прозрачности потенциального барьера называется величина
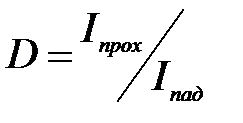 . (6.34)
. (6.34)
Примерами туннельного эффекта могут служить выбрасывание a-частицы из ядра радиоактивного атома; переход электрона из металла в вакуум.
Коэффициент прозрачности прямоугольного потенциального барьера:
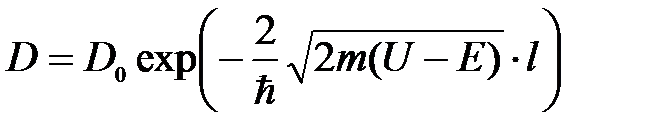 , (6.35)
, (6.35)
где D – коэффициент прозрачности потенциального барьера; D 0 – постоянный коэффициент, близкий к единице; m – масса частицы; Е – энергия частицы; l – ширина барьера; U – высота барьера, т.е. значение потенциальной энергии.
Коэффициент прозрачности барьера сложной формы:
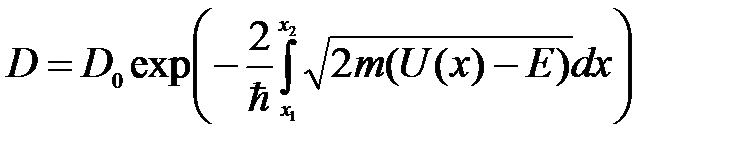 , (6.36)
, (6.36)
где x 1 и x 2 – координаты начала и конца барьера; U ( x ) – значение потенциальной энергии для данного значения полной энергии Е.
Примеры решения задач
Задача 1. Показать, что ограничение частицы в пространстве вызывает квантование ее энергии.
Решение
Рассмотрим частицу в одномерной потенциальной яме с бесконечно высокими стенками (см. рис.6.5).

|
| Рис. 6.5 |
Найдем волновую функцию частицы. Для нее мы ожидаем:
·Y (х) = 0 вне ямы;
· Y (0) = Y ( L ) = 0 на стенках ямы;
· Y (х) должна быть волной или суммой волн, т.к. представляет частицу и должна быть связана с деБройлевской волной.
Пусть волновая функция имеет вид:
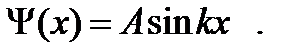
Она должна вписываться в «ящик» (рис.6.6):

|
| Рис.6.6. |
Это означает, что целое число полуволн должно укладываться на длине L
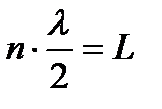
или возможные длины волн равны:
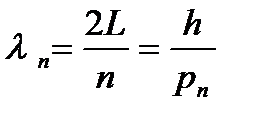 ,
,
где n = 1, 2, 3, …..
Отсюда получаем возможные значения импульсов частицы в яме:
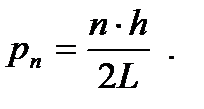
Полная энергия частицы в пределах ямы равна кинетической энергии, т.к. потенциальная энергия в яме U = 0 и частица является свободной:
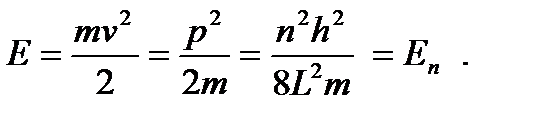
Итак, частица обладает не любой энергией, а вполне конкретной, зависящей от целого числа n
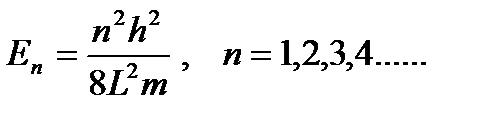 ,
,
где n – главное квантовое число.
Таким образом, действительно ограничение движения частицы в пространстве приводит к квантованию ее энергии. Это же должно быть справедливо и для электрона в атоме водорода.
Отметим, что энергия частицы с Е = 0 отсутствует, т.к. соответствующая ей волна не существует. Таким образом, минимальная энергии частицы в потенциальной яме соответствует состоянию с квантовым числом n=1:
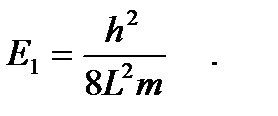
Задача 2. Частица находится в одномерном потенциальном ящике шириной L. Найти среднее положение частицы в основном состоянии.
Решение
По определению средняя координата частицы определяется из соотношения
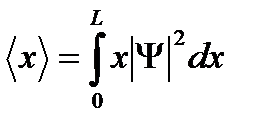
Волновая функция частицы в потенциальной яме (см. предыдущую задачу)
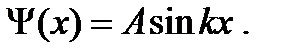
Из требования
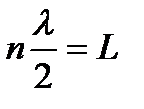
длина волны основного состояния, для которого n = 1, равна 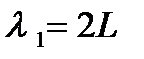 , а волновой вектор
, а волновой вектор
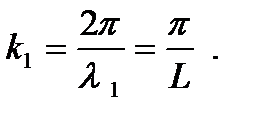
Волновая функция основного состояния имеет вид: 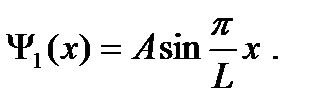
Волновая функция должна быть нормирована: 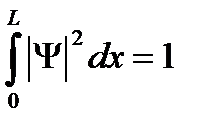 .
.
Из условия нормировки находим амплитуду волновой функции А:
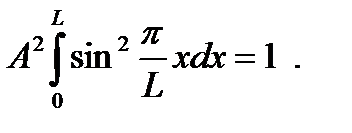
Вычислим интеграл:
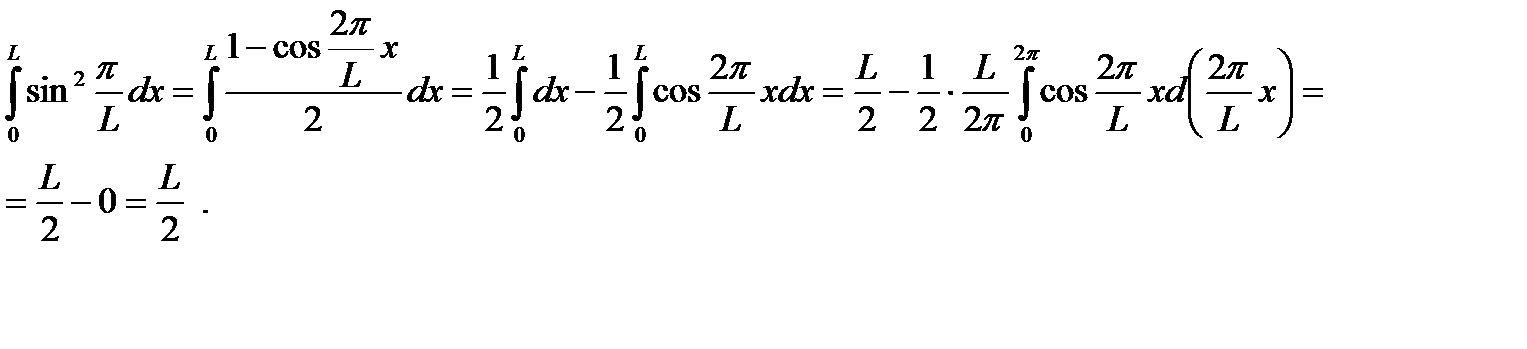
Получаем: 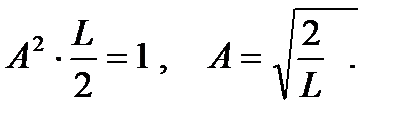
Итак, волновая функция основного состояния имеет вид:
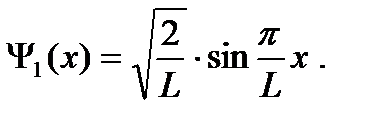
Находим среднюю координату частицы:
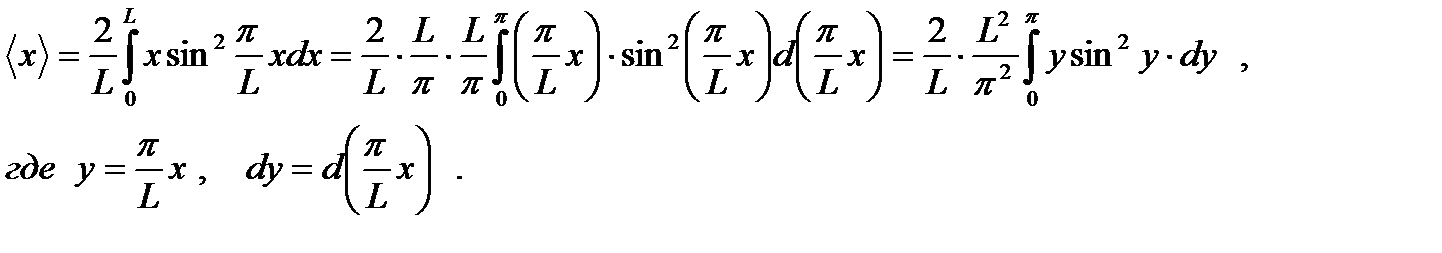
Вычислим интеграл:
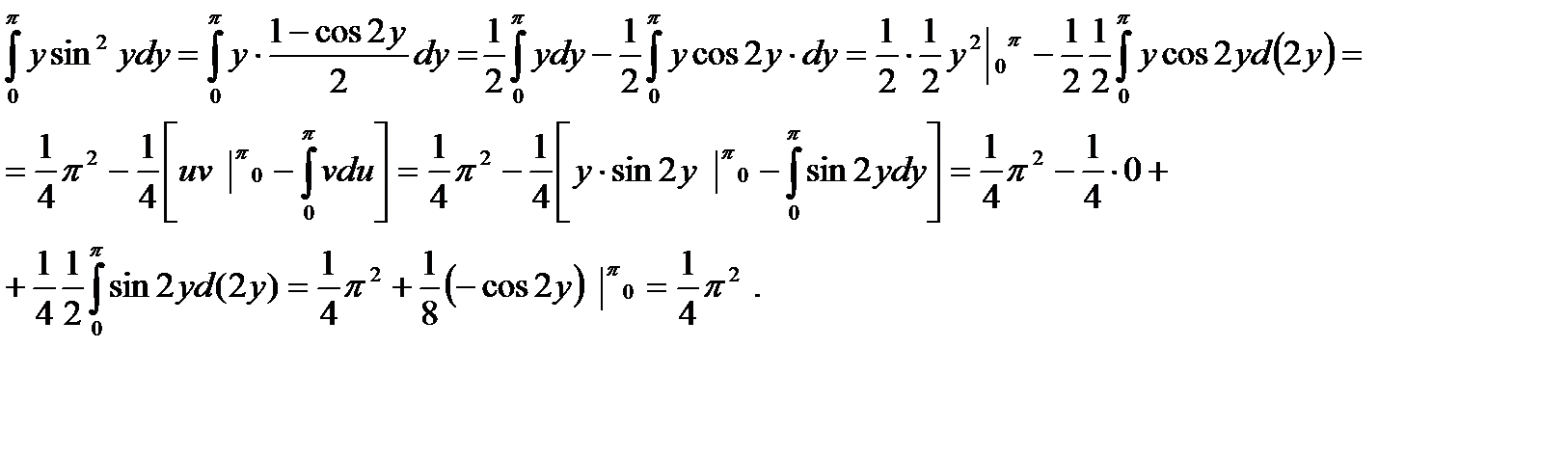
В результате получаем: 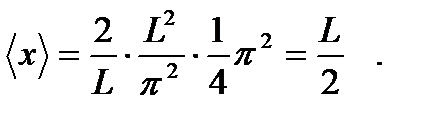
Видно, что частица находится в середине ящика, что и следует из плотности вероятности 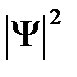 :
:

Рис. 6.7.
Задача 3. Какова ширина (l) одномерной потенциальной ямы с бесконечно высокими стенками, если при переходе электрона со второго квантового уровня (n1 = 2) на первый (n2 = 1) излучается фотон с энергией Е = 1 эВ?
| Дано: n1 = 2 n2 = 1 Е = 1 эВ | СИ: 1.6×10-19 Дж |
| l - ? |
Решение
Запишем уравнение для энергии электрона на заданных стационарных уровнях:
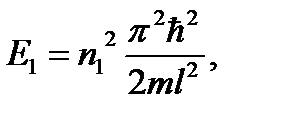
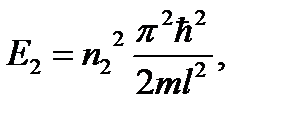
По условию задачи при указанном переходе выделяется квант энергии:
ΔЕ = Е1 – Е2.
Подставим значения соответствующих энергий и получим уравнение:
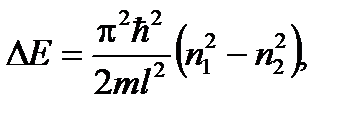
Из последнего уравнения выразим искомую величину – ширину ямы (l):
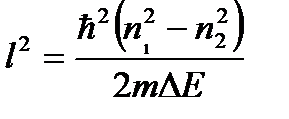
Подставим численные значения и сделаем расчет:
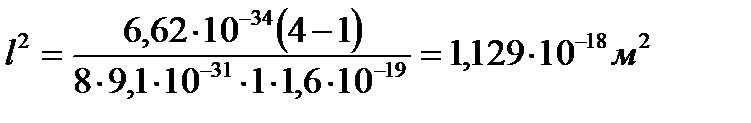
Ответ: l = 1,062 10-9 м.
Задача 4. При какой ширине (l) потенциальной ямы дискретность энергии микрочастицы, находящейся в ней, сравнима с энергией теплового движения при температуре Т.
Решение
Запишем уравнение для собственных энергий электрона в атоме для стационарных уровней с номерами n и (n + 1):
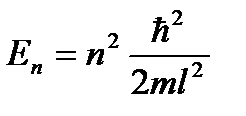 и
и 
Запишем дискретность энергии микрочастицы для указанных состояний с номерами n и (n + 1):
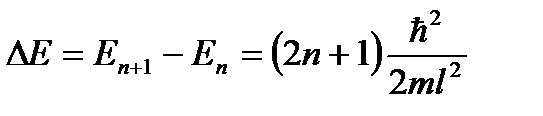
По условию 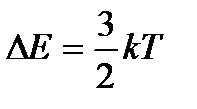 , поэтому можно записать:
, поэтому можно записать:
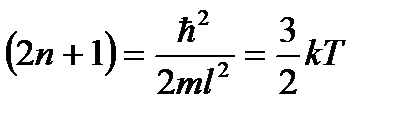
Решаем полученное уравнение относительно ширины ямы – l
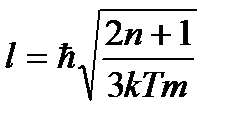
Ответ: 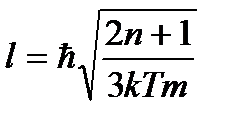
Задачи для самостоятельного решения
1. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность W нахождения частицы: 1) в средней трети ящика; 2) в крайней трети ящика?
2. Частица в потенциальном ящике шириной L находится в возбуждённом состоянии (n = 2). Определить, в каких точках интервала (0 < x < L) плотность вероятности |ψ n(x)|² нахождения частицы максимальна и минимальна?
3. Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины L с абсолютно непроницаемыми стенками (0<x<L). Найти вероятность пребывания частицы в области 1/3L £x£2/3L.
4. Электрон с длиной волны де Бройля l1 = 100 пм, двигаясь в положительном направлении оси X, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определите длину волны де Бройля после прохождения барьера.
5. Электрон находится в одномерной прямоугольной потенциальной «яме» шириной L с бесконечно высокими стенками. Определите вероятность обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 3).
6. Частица находится в основном состоянии одномерной прямоугольной ямы ширины L с абсолютно непроницаемыми стенками ( 0 < x > L ). Найти вероятность нахождения частицы в области 1/2L < x < 2/3L.
7. Прямоугольный потенциальный барьер имеет ширину L = 0.1 нм. Определите (в эВ) разность энергий U – E, при которой вероятность прохождения электрона сквозь барьер составит 0.5.
8. Частица в одномерной прямоугольной «потенциальной яме» шириной L с бесконечно высокими «стенками» находится в возбужденном состоянии (n= 3). Определите, в каких точках «ямы» плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните результат графически.
9. Математический маятник можно рассматривать в качестве гармонического осциллятора. Определите в электрон-вольтах энергию нулевых колебаний маятника длиной l = 1 м, находящегося в поле тяготения Земли.
10. Прямоугольный потенциальный барьер имеет ширину L = 0.1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси x электрона U – E = 5 эВ. Определите, во сколько раз изменится коэффициент прозрачности D потенциального барьера, если разность U – E возрастет в 4 раза.
Практические занятия 8-9
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Строение атома водорода в квантовой механике. Принцип запрета Паули. Многоэлектронные атомы».
2. Привитие навыков решения задач по данной теме.
Краткая теория
Примеры решения задач
Задача 1. Электрон в атоме находится в f-состоянии. Определите: 1) момент импульса электрона; 2) максимальное значение проекции момента импульса на направление внешнего магнитного поля.
| Дано: f -состояние |
| 1) Ll -? 2) ( Llz ) max -? |
Решение.
Состояние электрона характеризуется орбитальным квантовым числом l =3, а момент импульса (механический орбитальный момент) электрона равен:
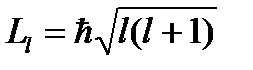 (1)
(1)
где 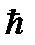 — постоянная Планка.
— постоянная Планка.
Проекция момента импульса на направление внешнего магнитного поля
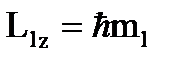 , (2)
, (2)
где ml = 0, ± 1, ± 2, ± 3, ….. ± l - магнитное квантовое число. Выражение (2) максимально при ml = ( ml ) max:
( Llz ) max = 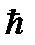 ( ml ) max (3)
( ml ) max (3)
где, по условию задачи, ( ml ) max = 3.
Подставив числовые значения, получаем:
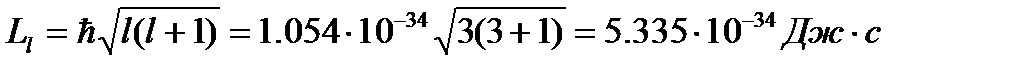
( Llz ) max = 1.054 × 10-34 × 3 = 3.162 × 10-34 Дж × с
Ответ: Ll = 5.335 × 10-34 Дж × с; ( Llz ) max = 3.162 × 10-34 Дж × с.
Задача 2. Сколько различных состояний может иметь электрон с главным квантовым числом n = 4?
| Дано: n = 4 |
| N - ? |
Решение.
При n=4 орбитальное квантовое число l может принимать значения 0, 1, 2, 3.
При l = 0 магнитное квантовое число ml может принимать только одно значение: ml = 0. Спиновое квантовое число ms может иметь два значения: ms = ½, -½. Cледовательно, в этом случае электрон может находиться в двух состояниях.
При l = 1 магнитное квантовое число ml может принимать значения: ml = 0, 1, -1, а магнитное квантовое число: ms = ½, -½. Поэтому общее число состояний электрона равно 6.
При l = 2 магнитное квантовое число ml может принимать значения: ml = 0, 1, -1, 2, -2, магнитное квантовое число: ms = ½, -½. Поэтому общее число состояний электрона на этом подуровне равно 10.
При l = 3 магнитное квантовое число ml может принимать значения: ml = 0, 1, -1, 2, -2, 3, -3, магнитное квантовое число: ms = ½, -½. Поэтому общее число состояний электрона на этом подуровне равно 14.
Общее число состояний, которые может иметь электрон с главным квантовым числом n = 4 равно: N = 2+6+10+14 = 32
Ответ: N = 32
Задача 3. Электрон в возбужденном атоме водорода находится в 3-d состоянии. Определите изменение орбитального магнитного момента электрона при переходе атома в основное состояние.
| Дано: l1 = 2 l2 = 0 |
| D pm - ? |
Решение.
Изменение орбитального магнитного момента равно:
D pm = pm 2 – pm 1 ,
где pm 1 и pm 2 – орбитальные магнитные моменты электрона в начальном (возбужденном) и конечном (основном) состояниях.
Модуль магнитного момента, обусловленного орбитальным движением электрона, равен:
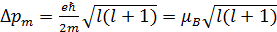 ,
,
где 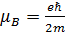 –магнетон Бора, l – орбитальное квантовое число.
–магнетон Бора, l – орбитальное квантовое число.
Учитывая значения l 1 и l 2 в возбужденном и основном состояниях, получаем:
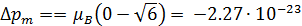 Дж/Тл.
Дж/Тл.
Знак «минус» показывает, что орбитальный магнитный момент уменьшается.
Ответ: Dpm = -2.27×10-23 Дж/Тл.
Задача 4. Пользуясь Периодической системой элементов, запишите электронную конфигурацию (распределение электронов по состояниям) атома брома, находящегося в основном состоянии.
Решение.
Согласно Периодической системе элементов, бром имеет порядковый номер 35, следовательно, электронная оболочка атома брома содержит 35 электронов.
Распределение электронов в атоме подчиняется принципу запрета Паули, в соответствии с которым два электрона, находящиеся в одном и том же атоме, не могут иметь одинаковый набор квантовых чисел.
Электронная конфигурация для атома брома запишется следующим образом:
1s22s22p63s23p63d104s24p5.
В данной записи цифры 1, 2, 3, 4 - главные квантовые числа, определяющие символ оболочки (соответственно K, L, M, N). Максимально возможное число электронов в K-оболочке 2, в L-оболочке – 8, в M-оболочке – 18, в N-оболочке – 32.
Обозначения 1s, 2s, 2p, 3s, 3p, 3d,... определяют символ подоболочки, при этом в s-состоянии может находиться 2 электрона, в р-состоянии – 6 электронов, в d-состоянии – 10 электронов.
К-оболочка (n =1, l = 0, ml = 0, ms = ± 1/2 )заполнена полностью и записывается, как 1s2 (то есть, на этой оболочке находятся два s - электрона).
Также полностью заполнены L- оболочка (2s22p6 – два 2s- электрона и шесть 2p-электронов) и M-оболочка (3s23p63d10 - два 3s-электрона, шесть 3p-электронов и десять 3d-электронов).
Оставшиеся семь электронов образуют незаполненную N – оболочку (4s24p5 – два 4s-электрона и пять 4р-электронов).
Ответ: 1s22s22p63s23p63d104s24p5.
Задачи для самостоятельного решения
1. Электрон в атоме находится в f-состоянии. Найти орбитальный момент импульса L ℓ электрона и максимальное значение проекции момента импульса (Ll , z)max на направление внешнего магнитного поля.
2. Момент импульса L ℓ орбитального движения электрона в атоме водорода равен 1,83∙10-34 Дж∙с. Определить магнитный момент Мℓ электрона, находящегося в 2р-состоянии в атоме водорода.
3. Используя принцип Паули, указать, какое максимальное число Nmax электронов в атоме могут иметь одинаковые следующие квантовые числа: 1) n, ℓ, m ℓ, ms; 2) n, ℓ, m ℓ; 3) n, ℓ; 4) n.
4. Найти число N электронов в атомах, у которых в основном состоянии заполнены: 1) K- и L-слои, 3s-оболочка и наполовину 3р-оболочка; 2) K-, L- и М- слои и 4s-, 4р- и 4d-оболочки. Что это за атомы?
5. Вычислить момент импульса L ℓ орбитального движения электрона, находящегося в атоме: 1) в s-состоянии; 2) в р-состоянии.
6. Определить возможные значения проекции момента импульса L ℓ z орбитального движения электрона в атоме на направление внешнего магнитного поля. Электрон находится в d –состоянии.
7. В атоме K, L и M оболочки заполнены полностью. Определите общее число электронов в атоме.
8. Найти число N электронов в атомах, у которых в основном состоянии заполнены: 1) K- и L-слои, 3s-оболочка и наполовину 3р-оболочка; 2) K-, L- и М- слои и 4s-, 4р- и 4d-оболочки. Что это за атомы?
9. Заполненной электронной оболочке соответствует главное квантовое число n= 4. Определите число электронов на этой оболочке, которые имеют одинаковое магнитное квантовое число ml = 0.
10. Определить возможные значения проекции момента импульса L ℓ z орбитального движения электрона в атоме на направление внешнего магнитного поля. Электрон находится в d –состоянии
Практические занятия 10-12
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Элементы квантовой статистики. Зонная структура твердых тел. Электропроводность полупроводников. Контактные явления».
2. Привитие навыков решения задач по данной теме.
Краткая теория
Применение квантовомеханического подхода к анализу поведения электрона в атоме водорода показало, что не только его энергия, но и связанный с движением вокруг ядра его момент импульса L, обусловленный этим же движением магнитный момент pm, а также проекции векторов  и
и  на направление внешнего магнитного поля могут принимать лишь вполне определенные дискретные значения, т.е. квантуются. Разрешенные значения этих величин определяются целочисленными параметрами n , l и m, называемыми квантовыми числами. Позднее к ним было добавлено еще одно квантовое число ms, которое определяет разрешенные значения проекции на направление внешнего магнитного поля так называемых спиновых момента импульса и магнитного момента, не связанных с движением электрона вокруг ядра, а присущих большинству элементарных частиц по самой их природе.
на направление внешнего магнитного поля могут принимать лишь вполне определенные дискретные значения, т.е. квантуются. Разрешенные значения этих величин определяются целочисленными параметрами n , l и m, называемыми квантовыми числами. Позднее к ним было добавлено еще одно квантовое число ms, которое определяет разрешенные значения проекции на направление внешнего магнитного поля так называемых спиновых момента импульса и магнитного момента, не связанных с движением электрона вокруг ядра, а присущих большинству элементарных частиц по самой их природе.
Для электронов в многоэлектронных атомах точное решение уравнения Шредингера невозможно. Применение приближенных методов показывает, что и в этом случае спектр энергии и других характеристик электрона является дискретным. Расселение электронов атома по разрешенным значениям энергии диктуется двумя основными принципами: стремлением каждого электрона занять состояние с наименьшей энергией и так называемым принципом запрета Паули, согласно которому в атоме не может быть двух электронов с одинаковым набором всех четырех квантовых чисел n , l , m и ms. Энергия электрона в многоэлектронном атоме зависит от двух первых квантовых чисел n и l, а при данном l возможны 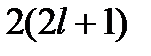 разрешенных состояний, отличающихся проекциями орбитальных и спиновых моментов на направление внешнего поля. Поэтому на уровне 1s (n =1, l =0) могут находиться до 2-х электронов, на уровне 2s (n =2, l =0) – тоже 2 электрона, на уровне 2р (n =2, l =1) – до 6 электронов и т.д. В такой последовательности и застраиваются энергетические уровни (электронные оболочки) многоэлектронных атомов, входящих в Периодическую систему элементов. В результате в каждом атоме имеется одна или несколько заполненных электронами оболочек и одна, последняя, - незаполненная (она называется валентной оболочкой и от ее строения зависят химические свойства элемента). Выше валентного уровня энергии в спектре атома имеется еще очень много так называемых возбужденных уровней, на которые электроны атома могут переходить под влиянием внешних воздействий. Схема расселения электронов по энергетическим уровням в атоме представлена на рис.10.1.
разрешенных состояний, отличающихся проекциями орбитальных и спиновых моментов на направление внешнего поля. Поэтому на уровне 1s (n =1, l =0) могут находиться до 2-х электронов, на уровне 2s (n =2, l =0) – тоже 2 электрона, на уровне 2р (n =2, l =1) – до 6 электронов и т.д. В такой последовательности и застраиваются энергетические уровни (электронные оболочки) многоэлектронных атомов, входящих в Периодическую систему элементов. В результате в каждом атоме имеется одна или несколько заполненных электронами оболочек и одна, последняя, - незаполненная (она называется валентной оболочкой и от ее строения зависят химические свойства элемента). Выше валентного уровня энергии в спектре атома имеется еще очень много так называемых возбужденных уровней, на которые электроны атома могут переходить под влиянием внешних воздействий. Схема расселения электронов по энергетическим уровням в атоме представлена на рис.10.1.
Если перейти от рассмотрения движения одной микрочастицы (одного электрона) к многоэлектронным системам, то проявляются особые свойства, не имеющие аналогов в классической физике. Пусть квантово-механическая система состоит из одинаковых частиц, например электронов. Все электроны имеют одинаковые физические свойства – массу, электрический заряд, спин и другие внутренние характеристики (например квантовые числа). Такие частицы называют тождественными.
Необходимые свойства системы одинаковых тождественных частиц проявляются в фундаментальном принципе квантовой механики – принципе неразличимости тождественных частиц, согласно которому невозможно экспериментально различить тождественные частицы.
 | |
| Рис. 10.1. Схема расселения электронов по энергетическим уровням в атоме |
В классической механике даже одинаковые частицы можно различить по положению в пространстве и импульсам. В квантовой механике положение иное. Из соотношения неопределенности вытекает, что для микрочастиц вообще неприменимо понятие траектории; состояние микрочастицы описывается волновой функцией, позволяющей лишь вычислять вероятность нахождения микрочастицы в окрестностях той или иной точки пространства. Если же волновые функции двух тождественных частиц в пространстве перекрываются, то разговор о том, какая частица находится в данной области, вообще лишен смысла: можно говорить лишь о вероятности нахождения в данной области одной из тождественных частиц. Таким образом, в квантовой механике тождественные частицы полностью теряют свою индивидуальность и становятся неразличимыми.
Если при перемене частиц местами волновая функция не меняет знака, то она называется симметричной, если меняет – антисимметричной. Изменение знака волновой функции не означает изменения состояния, т.к. физический смысл имеет лишь квадрат модуля волновой функции.
Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса: частицы с полуцелым спином (например электроны, нейтроны и протоны) описываются антисимметричными волновыми функциями и подчиняются статистике Ферми–Дирака; эти частицы называются фермионами. Частицы с нулевым, или целочисленным, спином (например фотоны, мезоны) описываются симметричными функциями (волновыми) и подчиняются статистике Бозе–Эйнштейна; эти частицы называются бозонами.
Сложные частицы (например атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спин – полуцелый), а из четного – бозонами (суммарный спин – целый).
Распределение электронов по различным квантовым состояниям подчиняется принципу Паули, согласно которому в одном состоянии не может быть двух одинаковых (с одинаковым набором четырех квантовых чисел) электронов, они должны отличаться какой-то характеристикой, например направлением спина. Следовательно, по квантовой теории, электроны в металле не могут располагаться на самом низшем энергетическом уровне даже при 0 К. Согласно принципу Паули, электроны вынуждены взбираться вверх «по энергетической лестнице».
Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энергия Ферми EF, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно отсчитывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых электронами энергетических уровней.
Для металлов при не слишком высоких температурах выполняется неравенство kT < ЕF. Это означает, что электронный газ в металлах практически всегда находится в состоянии сильного вырождения. Температура Т0 вырождения находится из условия kT0 = EF. Она определяет границу, выше которой квантовые эффекты перестают быть существенными. Соответствующие расчеты показывают, что для электронов в металле Т0 = 104 К, т. е. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден.
Примеры решения задач
Задача 1. Определите положение уровня Ферми в германии n- типа при температуре 300К, если на 1×106 атомов германия приходится 1 атом примеси. Обоснуйте сделанные при этом допущения.
Решение
В германии концентрация атомов равна 4,4×1028 м-3, концентрацию примесных атом найдем из пропорции
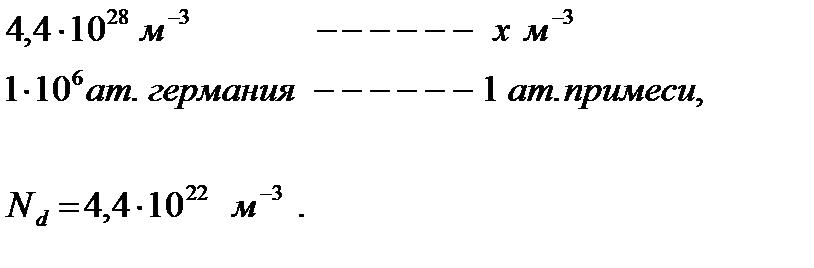
При температуре 300К все примесные атомы ионизованы и концентрация основных носителей заряда равна концентрации доноров 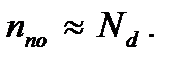
С другой стороны, концентрация основных носителей в примесном полупроводнике донорного типа определяется соотношением
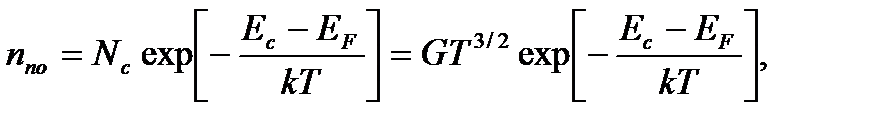
где 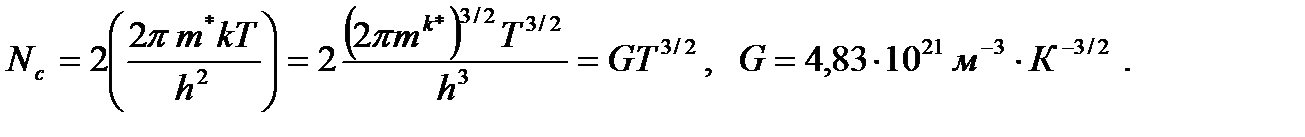
Здесь G – константа, связывающая число электронов в единице объема в зоне проводимости с температурой и энергией уровней.
Из выше приведенного выражения находим
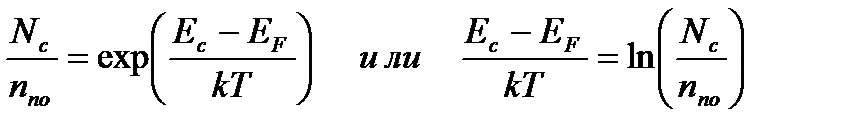 .
.
Отсюда получаем (Nc = 25×1024 м-3)
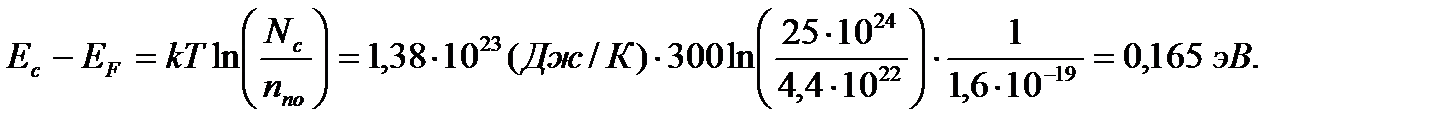
Это означает, что уровень Ферми находится на 0,165 эВ ниже дна зоны проводимости.
Задача 2. В кремниевом образце дырочная и электронная области pn – перехода имеют удельное сопротивление 0,013 и 44,5 Ом×см соответственно. Определите, чему равен потенциальный барьер на переходе при комнатной температуре. В кремнии подвижности дырок и электронов равны mp = 480 и mn = 1400 см2/ В×с, а концентрация собственных носителей составляет 1,6×1010 см-3.
Решение
1. Удельные проводимости материалов p- и n–типа определяются следующими выражениями:
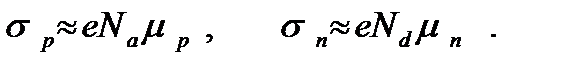
Удельные сопротивления равны
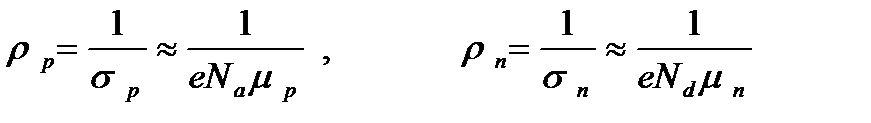 .
.
Откуда находим концентрации акцепторов и доноров
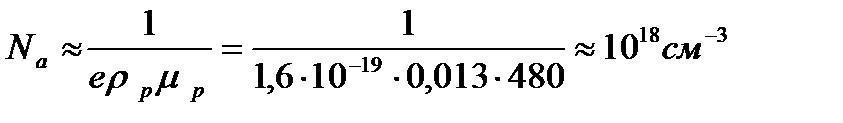 ;
;
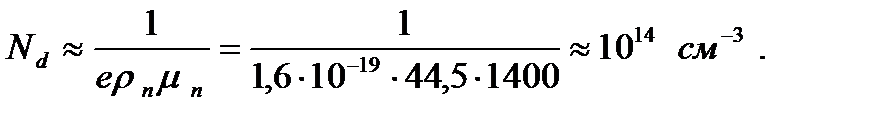
2.Находим высоту потенциального барьера
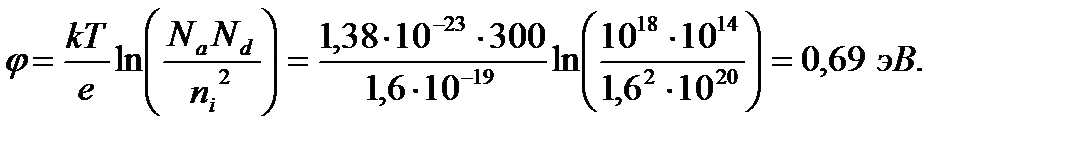
Задача 3. Удельная проводимость кремниевого образца при нагревании от температуры 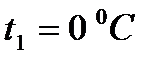 до температуры
до температуры 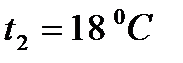 увеличилась в 4,24 раза. Определить ширину запрещенной зоны кремния.
увеличилась в 4,24 раза. Определить ширину запрещенной зоны кремния.
Решение.
Удельная проводимость собственных полупроводников
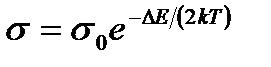 ,
,
где 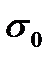 – постоянная, характерная для данного полупроводника;
– постоянная, характерная для данного полупроводника; 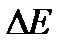 – ширина запрещенной зоны.
– ширина запрещенной зоны.
Тогда
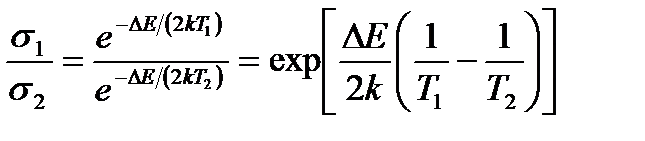
или, прологарифмировав,
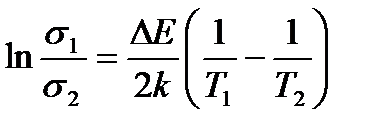 ,
,
откуда искомая ширина запрещенной зоны
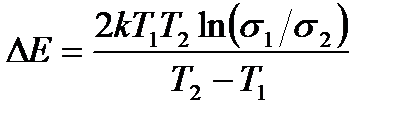 .
.
Вычисляя, получаем 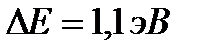 .
.
Задача 4. Вычислить максимальную энергию 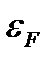 (энергию Ферми), которую могут иметь свободные электроны в металле (медь) при температуре
(энергию Ферми), которую могут иметь свободные электроны в металле (медь) при температуре 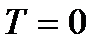 К. Принять, что на каждый атом меди приходится по одному валентному электрону.
К. Принять, что на каждый атом меди приходится по одному валентному электрону.
Решение.
Максимальная энергия 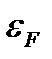 , которую могут иметь электроны в металле при
, которую могут иметь электроны в металле при  К, связана с концентрацией свободных электронов соотношением
К, связана с концентрацией свободных электронов соотношением
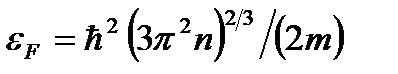 , (1)
, (1)
где  – постоянная Планка;
– постоянная Планка;  – масса электрона.
– масса электрона.
Концентрация свободных электронов по условию задачи равна концентрации атомов, которая может быть найдена по формуле
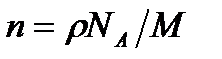 , (2)
, (2)
где  – плотность меди;
– плотность меди;  – постоянная Авогадро;
– постоянная Авогадро;  – молярная масса.
– молярная масса.
Подставляя выражение  в формулу (1), получаем
в формулу (1), получаем
 .
.
Произведем вычисления:
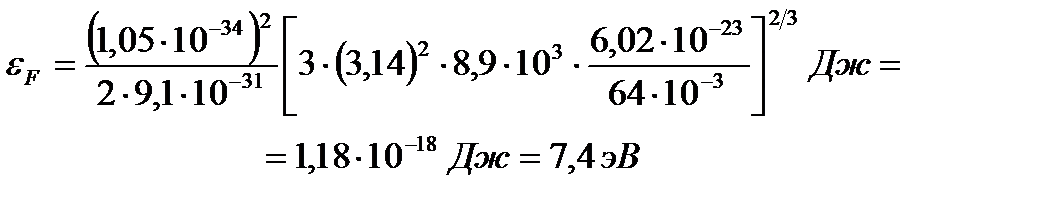
Задачи для самостоятельного решения
1. Германиевый образец нагревают от 0 до 17 С. Принимая ширину запрещенной зоны германия DE = 0.72 эВ, определите, во сколько раз возрастает его удельная проводимость.
2. Определите ширину запрещенной зоны собственного полупроводника, если при температуре Т1 и Т2 (Т2 > Т1) его сопротивление соответственно равно R1 и R2.
3. Нарисуйте на зонной схеме положение уровня Ферми для электронного и дырочного полупроводников: 1) при 0 К; 2) при повышении температуры. Объясните.
4. Определить уровень Ферми в собственном полупроводнике, если энергия активации DЕ0 = 0.1 эВ. За нулевой уровень отсчета кинетической энергии электронов принять низший уровень зоны проводимости.
5. Определить концентрацию электронов и дырок при Т=300 К: а) в собственном кремниевом полупроводнике; б) в кристалле кремния, содержащем 5×1017 атомов сурьмы в 1 см3
6. Определить долю свободных электронов в металле при T = 0 К, энергии E которых заключены в интервале значений от ½ Emax до Emax.
7. Определить концентрацию свободных электронов в металле при температуре 0 К. Энергию Ферми принять равной 1 эВ.
8. Оценить температуру вырождения Ткр для калия, если принять, что на каждый атом приходится по одному свободному электрону. Плотность калия 860 кг/м3.
9. Температура вырождения электронного газа в серебре составляет 63,6 кК. Какова концентрация свободных электронов в металле?
10. Собственный полупроводник (германий) имеет удельное сопротивление r=0.48 Ом∙м. Определите концентрацию носителей заряда n, если подвижности электронов и дырок, соответственно, равны 0.36 и 0.16 м2/(В∙с).
Практические занятия 13-14
Цель:
1. Закрепление теоретических знаний дисциплины по теме: «Закон радиоактивного распада. Ядерные реакции. Фундаментальные взаимодействия. Элементарные частицы».
2. Привитие навыков решения задач по данной теме.
Краткая теория
Атомное ядро состоит из элементарных частиц — протонов и нейтронов. Протонно-нейтронная модель ядра была предложена российским физиком Д.Д. Иваненко (1904-1994), а впоследствии развита В. Гейзенбергом).
Протон (р) имеет положительный заряд, равный заряду электрона, и массу mр = 1,6726×10-27 кг »1836 mе, где mе - масса электрона. Нейтрон (n) – электронейтральная частица с массой mn = 1,6749×10-27 кг »1839 mе. Протоны и нейтроны называются нуклонами (от лат. nucleus - ядро). Общее число нуклонов в атомном ядре называется массовым числом А.
Атомное ядро характеризуется зарядом Ze, где Z - зарядовое число ядра, равное числу протонов в ядре и совпадающее с порядковым номером химического элемента в Периодической системе элементов Д. И. Менделеева. Ядро обозначается тем же символом, что и нейтральный атом:  , где X - символ химического элемента, Z - зарядовое число (число протонов в ядре), А - массовое число (число нуклонов в ядре).
, где X - символ химического элемента, Z - зарядовое число (число протонов в ядре), А - массовое число (число нуклонов в ядре).
Так как атом нейтрален, то заряд ядра определяет и число электронов в атоме. От числа же электронов зависит их распределение по состояниям в атоме, от которого, в свою очередь, зависят химические свойства атома. Следовательно, заряд ядра определяет специфику данного химического элемента, то есть, определяет число электронов в атоме, конфигурацию их электронных оболочек, величину и характер внутриатомного электрического поля. Ядра с одинаковыми Z, но разными А (то есть, с разными числами нейтронов N = А - Z) называются изотопами, а ядра с одинаковыми А, но разными Z - изобарами.
В первом приближении ядро можно считать шаром, причем радиус ядра задается эмпирической формулой:
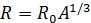 , (13.1)
, (13.1)
Радиус ядра имеет условный смысл, так как границы ядра размыты. Из формулы (13.1) следует, что объем ядра пропорционален числу нуклонов в ядре. Следовательно, плотность ядерного вещества примерно одинакова для всех ядер (r»1017 кг/м3).
Масса ядра измеряется в атомных единицах массы (а.е.м). За одну атомную единицу массы принимается 1/12 часть массы нейтрального атома углерода 12С:
1а.е.м = 1.6606 10-27 кг. (13.2)
А.е.м. выражается через энергетические единицы:
1а.е.м = 1.510-3 эрг = 1.510-10Дж = 931.49 МэВ (13.3)
Исследования показывают, что атомные ядра являются устойчивыми образованиями. Это означает, что в ядре между нуклонами существует определенная связь.
Между составляющими ядро нуклонами действуют особые, специфические для ядра силы, значительно превышающие кулоновские силы отталкивания между протонами. Они называются ядерными силами. Экспериментально установлено, что ядерные силы намного превышают гравитационные, электрические и магнитные взаимодействия и не сводятся к ним. Ядерные силы относятся к классу так называемых сильных взаимодействий.
Основные свойства ядерных сил:
1) ядерные силы являются силами притяжения;
2) ядерные силы являются короткодействующими — их действие проявляется только на расстоянии примерно 10~15 м. При увеличении расстояния между нуклонами ядерные силы быстро уменьшаются до нуля, а при расстояниях, меньших их радиуса действия, оказываются примерно в 100 раз больше кулоновских сил, действующих между протонами на том же расстоянии;
3) ядерным силам свойственна зарядовая независимость: ядерные силы, действующие между двумя протонами, или двумя нейтронами, или, наконец, между протоном и нейтроном, одинаковы по величине. Отсюда следует, что ядерные силы имеют неэлектрическую природу;
4) ядерным силам свойственно насыщение, т. е., каждый нуклон в ядре взаимодействует только с ограниченным числом ближайших к нему нуклонов.
5) ядерные силы зависят от взаимной ориентации спинов взаимодействующих нуклонов.
6) ядерные силы не являются центральными.
Экспериментально установлено, что масса ядра всегда меньше суммы масс составляющих его нуклонов. Но так как всякому изменению массы соответствует изменение энергии (Е = mc 2), то, следовательно, при образовании ядра должна выделяться определенная энергия. Из закона сохранения энергии вытекает и обратное: для разделения ядра на составные части необходимо затратить такое же количество энергии, которое выделяется при его образовании. Энергия, которую нужно затратить, чтобы расщепить ядро на отдельные нуклоны, называется энергией связи ядра.
Энергия связи нуклонов в ядре равна:
Есв = [Zmp + (A - Z)mn - m я )]c2, (13.4)
где mp, mn , m я – массы протона, нейтрона и ядра, соответственно.
Энергия связи ядра, выраженная через массу атома m, имеет вид:
Есв = [ZmH + (A - Z)mn -m]c2, (13.5)
где mH - масса атома водорода.
Уде льная энергия связи ядра  (A, Z) - это энергия связи, приходящаяся на один нуклон:
(A, Z) - это энергия связи, приходящаяся на один нуклон:
 (A, Z) = Eсв(A,Z) / A. (13.6)
(A, Z) = Eсв(A,Z) / A. (13.6)
На рис. 13.1 показана зависимость удельной энергии связи ядра  от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A ~55 - 60). Такой ход зависимости
от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A ~55 - 60). Такой ход зависимости  (A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а для тяжелых - деление на более легкие осколки.
(A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а для тяжелых - деление на более легкие осколки.
Рис.13.1. Зависимость удельной энергии связи ядра от числа нуклонов.
Изб ыток масс (дефект масс) D m – величина, на которую уменьшается масса всех нуклонов при образовании из них атомного ядра:
D m = [Zmp + (A - Z)mn] - m я. (13.7)
Способность ядер самопроизвольно распадаться, испуская частицы, называется радиоактивностью. Радиоактивный распад - статистический процесс. Каждое радиоактивное ядро может распасться в любой момент и закономерность наблюдается только в среднем, в случае распада достаточно большого количества ядер.
Радиоактивность подразделяется на естественную (наблюдается у неустойчивых изотопов, существующих в природе) и искусственную (наблюдается у изотопов, полученных посредством ядерных реакций). Принципиального различия между этими двумя типами радиоактивности нет, так как законы радиоактивного превращения в обоих случаях одинаковы.
Радиоактивное излучение бывает трех типов: a-, b- и g-излучение.
а-Излучение представляет собой поток ядер гелия; заряд a-частицы равен +2е, а масса совпадает с массой ядра изотопа гелия 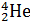 . а-Излучение отклоняется электрическим и магнитным полями, обладает высокой ионизирующей способностью и малой проникающей способностью.
. а-Излучение отклоняется электрическим и магнитным полями, обладает высокой ионизирующей способностью и малой проникающей способностью.
b -Излучение представляет собой поток быстрых электронов. b-Излучение отклоняется электрическим и магнитным полями; его ионизирующая способность значительно меньше (примерно на два порядка), а проникающая способность гораздо больше, чем у а-частиц.
g -Излучение представляет собой коротковолновое электромагнитное излучение с длиной волны l < 10-10 м и вследствие этого - ярко выраженными корпускулярными свойствами, т.е., является потоком частиц g-квантов (фотонов). Это излучение не отклоняется электрическим и магнитным полями, обладает относительно слабой ионизирующей способностью и очень большой проникающей способностью, испытывает дифракцию при прохождении через кристаллы.
Радиоактивный распад - это естественное радиоактивное превращение ядер, происходящее самопроизвольно. Атомное ядро, испытывающее радиоактивный распад, называется материнским, возникающее ядро - дочерним. Радиоактивный распад является спонтанным процессом, подчиняющимся статистическим законам.
Постоянная распада λ – это вероятность распада ядра в единицу времени.
Если в образце в момент времени t имеется N радиоактивных ядер, то количество ядер dN, распавшихся за время dt пропорционально N:
dN = -λNdt . (13.8)
Проинтегрировав это выражение, получим закон радиоактивного распада:
N ( t ) = N 0 e - l t , (13.9)
где N0 - количество радиоактивных ядер в момент времени t0 = 0.
Cреднее время жизни τ:
 . .
| (13.10) |
Период полураспада T1/2 – это время, за которое первоначальное количество радиоактивных ядер уменьшится в два раза:
T1/2 = ln2/ l = 0.693/ l = t ln2. (13.11)
Активность A нуклида – это среднее количество ядер, распадающихся в единицу времени:
A(t) = l N(t). (13.12)
Активность измеряется в кюри (Ки) и беккерелях (Бк):
1 Ки = 3.7·1010 распадов/c, 1 Бк = 1 распад/c.
Ядерные реакции - это превращения атомных ядер при взаимодействии с элементарными частицами (в том числе и с g-квантами) или друг с другом. В общем виде ядерную реакцию можно записать в форме
a1 + a2  b1 + b2 + ..., (13.13)
b1 + b2 + ..., (13.13)
где a1 и a2 - частицы, вступающие в реакцию, а b1, b2 ... - частицы, образующиеся в результате реакции.
Наиболее распространенным видом реакции является реакция с двумя частицами в конечном состоянии
а + A  b + B, (13.14)
b + B, (13.14)
или в сокращенной записи
A(a, b)B.
В такой записи обычно a - налетающая (обычно легкая) частица (ядро), A - ядро мишени, b- регистрируемая частица, B - конечное ядро.
В любой ядерной реакции выполняются законы сохранения зарядовых и массовых чисел: сумма зарядовых чисел (и сумма массовых чисел) ядер и частиц, вступающих в ядерную реакцию, равна сумме зарядовых чисел (и сумме массовых чисел) конечных продуктов (ядер и частиц) реакции. Выполняются также законы сохранения энергии, импульса и момента импульса.
Ядерные реакции могут быть как экзотермическими (с выделением энергии), так и эндотермическими (с поглощением энергии).
Энерг ия реакции - это скалярная физическая величина, являющаяся энергетической характеристикой ядерных превращений и равная разности энергий покоя ядер и частиц до и после реакции:
W = ( W 01 + W 02 ) – ( W 03 + W 04 ) (13.15)
При W > 0 реакции идут с выделением энергии (кинетическая энергия продуктов реакции превышает кинетическую энергию частиц и ядер до реакции. W < 0 реакции идут с поглощением энергии. Во втором случае первоначальная кинетическая энергия исходных продуктов должна превышать величину |Q|, которая называется порогом реакции.
Возможны два принципиально различных способа освобождения ядерной энергии.
1. Деление тяжелых ядер. В отличие от радиоактивного распада ядер, сопровождающегося испусканием α- или β-частиц, реакции деления – это процесс, при котором тяжелое ядро под действием нейтронов или других частиц делится на два крупных фрагмента сравнимых масс.
Деление ядер сопровождается испусканием вторичных нейтронов (нейтронов деления), которые могут вызвать новые акты деления, что делает возможным осуществление цепной реакции деления – ядерной реакции, в которой частицы, вызывающие реакцию, образуются как продукты этой реакции. Цепная реакция деления характеризуется коэффициентом размножения ( k ) нейтронов, который численно равен отношению числа нейтронов в данном поколении к их числу в предыдущем поколении.
Необходимым условием для осуществления цепной реакции является требование: k³1. При k > 1 идет развивающаяся реакция, число делений непрерывно растет и реакция может стать взрывной. При k = 1 осуществляется самоподдерживающаяся реакция, при которой число нейтронов не меняется с течением времени. При k < 1 идет затухающая реакция.
2. Термоядерные реакции. Второй путь освобождения ядерной энергии связан с реакциями синтеза. При слиянии легких ядер и образовании нового ядра должно выделяться большое количество энергии. Вплоть до ядер с массовым числом около 60 удельная энергия связи нуклонов растет с увеличением A. Поэтому синтез любого ядра с A < 60 из более легких ядер должен сопровождаться выделением энергии. Общая масса продуктов реакции синтеза будет в этом случае меньше массы первоначальных частиц.
Реакции слияния легких ядер носят название термоядерных реакций, так как они могут протекать только при очень высоких температурах. Чтобы два ядра вступили в реакцию синтеза, они должны сблизится на расстояние действия ядерных сил порядка 2·10–15 м, преодолев электрическое отталкивание их положительных зарядов. Для этого средняя кинетическая энергия теплового движения молекул должна превосходить потенциальную энергию кулоновского взаимодействия. Расчет необходимой для этого температуры T приводит к величине порядка 108–109 К. Это чрезвычайно высокая температура. При такой температуре вещество находится в полностью ионизированном состоянии, которое называется плазмой.
Элементарные частицы объединяются в три группы: фотоны, лептоны и адроны.
Группа фотонов состоит из одной частицы - фотона - кванта электромагнитного взаимодействия.
Группа лептонов состоит из электрона, мюона, электронного и мюонного нейтрино, тяжелого лептона - τ -лептона (таона), таонного нейтрино, а также соответствующих им античастиц. Они участвуют только в электромагнитном и слабом взаимодействиях.
К группе адронов относятся мезоны (пионы и каоны) и барионы (нуклоны (протон, нейтрон) и нестабильные частицы). При распаде бариона, наряду с другими частицами, всегда образуется новый барион - закон сохранения барионного заряда. Адроны обладают сильным взаимодействием, наряду с электромагнитным и слабым.
Адроны состоят из кварков. Каждый мезон M строится из одного кварка q и одного антикварка 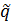 , каждый барион B - из трех кварков q : M = q
, каждый барион B - из трех кварков q : M = q 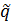 , B = qqq/
, B = qqq/
Число лептонов равно числу типов кварков - принцип кварк-лептонной симметрии.
Имеются кварки шести типов, которые подобно лептонам образуют три дублета, или три поколения (u,d) , (c,s), (t,b) :
1) верхний (up) — u
2) нижний (down) — d
3) "очарованный" (charm) — c
4) "странный" (strange) — s
5) "истинный" (true) — t
6) "прелестный" (beauty) —b.
У кварков имеются античастицы - антикварки.
Для определения полной энергии и импульса релятивистской частицы используются формулы:
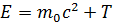
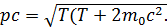 (13.16)
(13.16)
При рассмотрении столкновения частиц полезно использовать инвариантную величину:
Е2 –р2с2 = mo 2 c 4 , (13.17)
где Е и р – энергия и импульс системы до взаимодействия, mo – масса покоя образовавшейся частицы.
Пороговая (минимальная) кинетическая энергия частицы m, налетающей на покоящуюся частицу М, для возбуждения эндоэнергетической реакции m + M ® m 1 + m 2 +…:
 (13.18)
(13.18)
где m , M , m 1 , m 2 , … – массы покоя соответствующих частиц.
Квантовые числа, приписываемые элементарным частицам:
Q – электрический заряд;
L – лептонный заряд;
В – барионный заряд;
Т – изотопический спин, Tz – его проекция;
S – странность; S = 2< Q > - В;
Y - гиперзаряд, Y = S + B.
Связь между квантовыми числами сильно взаимодействующих частиц:
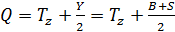 (13.19)
(13.19)
При взаимодействии частиц выполняются законы сохранения Q , L и В зарядов. В сильных взаимодействиях выполняются также законы сохранения S (или Y), T и его проекции Tz.
Примеры решения задач.
Задача 1. Эмпирическая зависимость радиуса ядра R от числа нуклонов A (A>10) R  r0A1/3. Параметр r0
r0A1/3. Параметр r0  1.23·10-13 см = 1.23 Фм приблизительно одинаков для всех ядер. Оценить радиусы атомных ядер 27Al, 90Zr, 238U.
1.23·10-13 см = 1.23 Фм приблизительно одинаков для всех ядер. Оценить радиусы атомных ядер 27Al, 90Zr, 238U.
Дан о :
A (A>10) R  r0A1/3
r0 r0A1/3
r0 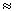 1.23·10-13 см
27 Al, 90Zr, 238U 1.23·10-13 см
27 Al, 90Zr, 238U
| СИ: 1.23·10-1 5 м |
| R - ? |
Решение.
Для 27Al:
R = 1.23×10-15 271/3 =3.69×10-15 м » 3.7 Фм.
Для 90Zr:
R = 1.23×10-15 901/3 =5.51×10-15 м »5.5 Фм.
Для 238U:
R = 1.23×10-15 2381/3 = 7.62×10-15 м »7.6 Фм.
Ответ: R (27Al) = 3.7 Фм, R (90Zr) = 5.5 Фм, R (2238U) = 7.6 Фм.
Задача 2. Масса нейтрально атома 16O mат(A, Z) = 15.9949 а.е.м. Определить удельную энергию связи e ядра 16O.
| Дано: mат(A,Z) = 15.9949 а.е.м. |
| e - ? |
Решение.
Удельная энергия связи ядра
 ( A , Z ) = E св ( A , Z )/ A ,
( A , Z ) = E св ( A , Z )/ A ,
где Eсв(A, Z) - энергия связи ядра, A - массовое число.
Полная энергия связи ядра:
E св ( A , Z ) = [ Zmp + ( A - Z ) mn - m я ( A , Z )] c 2 = [ Zmp + ( A - Z ) mn - m ат ( A , Z ) - Zme ] c 2 .
Используя энергетические единицы для массы 1а.е.м.= 931.49 МэВ, получаем для ядра 16O
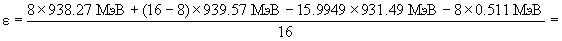
= 7.5 МэВ/нуклон.
Задача3. Во сколько раз число распадов ядер радиоактивного иода 131I в течение первых суток больше числа распадов в течение вторых суток? Период полураспада изотопа 131I равен 193 часам.
| Дано : t = 1 сут. 131I T1/2 = 193 ч. |
| N1/N2 - ? |
Решение.
Из закона радиоактивного распада
N(t) = N0 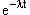
следует, что в течение первых суток (первых 24 часов) распалось число ядер, равное:
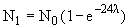
В течение вторых суток распалось число ядер: 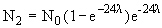
Отношение числа распадов за первые сутки к числу распадов за вторые сутки равно:
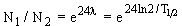 ,
,
где T1/2- период полураспада 131I в часах, связанный с l соотношением:
T1/2 = ln2/ 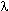 = 0.693/
= 0.693/ 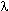 .
.
Окончательно получаем:
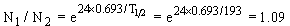 .
.
Ответ: N1/N2 =1.09.
Задача4. Определить энергию W, выделяемую 1 мг препарата 210Po за время, равное среднему времени жизни, если при одном акте распада выделяется энергия E = 5.4 МэВ.
| Дано: m = 1 мг 210 Po t = tcp E = 5.4 МэВ |
| W - ? |
Решение.
Количество ядер радиоактивного препарата за среднее время жизни уменьшается в e = 2.718 раз.
Тогда количество распавшихся за это время ядер будет D = 1 - 1/2.718 = 0.632 от их первоначального числа.
Начальное число ядер N в образце массой m грамм определяется из соотношения N = mNA/A, где NA - число Авогадро, A - массовое число.
Количество энергии, выделившейся за время, равное среднему времени жизни изотопа 210Po:
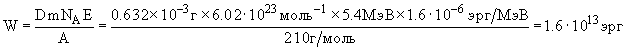 Ответ: W = 1.6×1013 эрг.
Ответ: W = 1.6×1013 эрг.
Задача5. Какие из нижеследующих процессов запрещены законом сохранения лептонного заряда:
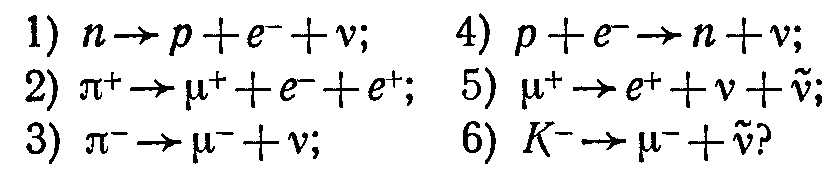
Решение
(1) Процесс 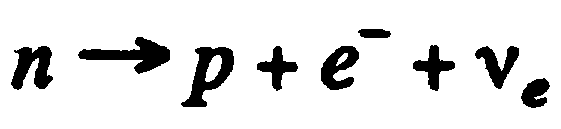 не может реализовываться, поскольку имеются два лишних лептона
не может реализовываться, поскольку имеются два лишних лептона 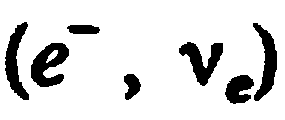 справа, а в левой стороне число их равно нулю.
справа, а в левой стороне число их равно нулю.
(2) Процесс  запрещен, потому что он соответствует изменению лептонного числа ( 0 – слева, -1 – справа).
запрещен, потому что он соответствует изменению лептонного числа ( 0 – слева, -1 – справа).
(3) Процесс  запрещен, потому что
запрещен, потому что  являются лептонами и мы имеем DL=2.
являются лептонами и мы имеем DL=2.
(4), (5), (6) процессы разрешены (за исключением того, что мы должны делать различие между мюонным нейтрино и электронным нейтрино).
Задачи для самостоятельного решения
1. Определите энергию связи ядра 177N. Примите массу ядра азота равной 2,325×10-26 кг. Ответ выразите в электрон-вольтах.
2. Определите энергию, которую необходимо затратить, чтобы разделить ядро дейтрона на протон и нейтрон. Массу ядра дейтрона принять равной 3,343×10-27 кг. Ответ выразите в электрон-вольтах.
3. Найти энергию связи W ядра изотопа лития  .
.
4. Найти энергию связи W ядра атома гелия 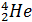 .
.
5. Найти энергию связи W ядра атома алюминия 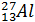 .
.
6. Найти энергию связи W0 , приходящуюся на один нуклон в ядрах: а) 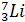 ; б)
; б) 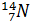 ; в)
; в) 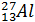 ; г)
; г) 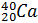 ; д)
; д) 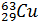 ; е)
; е) 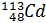 ; ж)
; ж) 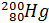 ; з)
; з) 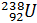 . Построить зависимость W0 = f (A).
. Построить зависимость W0 = f (A).
7. Определить сечение  реакции 31P(n,p)31Si, если известно, что после облучения мишени 31P толщиной d = 1 г/см2 в потоке нейтронов J = 2·1010 с-1·см-2 в течение времени tобл = 4 ч ее
реакции 31P(n,p)31Si, если известно, что после облучения мишени 31P толщиной d = 1 г/см2 в потоке нейтронов J = 2·1010 с-1·см-2 в течение времени tобл = 4 ч ее  -активность I, измеренная через время tохл = 1 час после окончания облучения, оказалась I(tохл) = 3.9·106 распадов/с. Период полураспада T1/2(31Si) = 157.3 мин.
-активность I, измеренная через время tохл = 1 час после окончания облучения, оказалась I(tохл) = 3.9·106 распадов/с. Период полураспада T1/2(31Si) = 157.3 мин.
8. Определить кинетические энергии  -частиц
-частиц 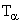 , образующихся при
, образующихся при  - распаде 212Bi на возбужденные состояния ядра 208Tl с энергиями 0,49 и 0,61 МэВ. Энергия связи Eсв.(A,Z) ядра 212Bi - 1654.32 МэВ, ядра 208Tl - 1632.23 МэВ и
- распаде 212Bi на возбужденные состояния ядра 208Tl с энергиями 0,49 и 0,61 МэВ. Энергия связи Eсв.(A,Z) ядра 212Bi - 1654.32 МэВ, ядра 208Tl - 1632.23 МэВ и  -частицы - 28.30 МэВ.
-частицы - 28.30 МэВ.
9. Используя значения масс атомов, определить верхнюю границу спектра позитронов, испускаемых при 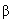 + -распаде ядра 27Si.
+ -распаде ядра 27Si.
10. Определить энергию отдачи ядра 7Li, образующегося при e- захвате в ядре 7Be. Даны энергии связи ядер - Eсв(7Be) = 37.6 МэВ, Eсв(7Li) = 39.3 МэВ.
СПИСОК ЛИТЕРАТУРЫ
а) основная литература
1. Трофимова Т. И. Курс физики: учеб. пособие для вузов / Т. И. Трофимова. - 18-е изд., стереотип. - М.: Академия, 2010.
2. Трофимова Т. И. Курс физики: учеб. пособие для вузов / Т. И. Трофимова. - 15-е изд., стереотип. - М.: Academia, 2007.
3. Никеров В.А. Физика. Современный курс. - М.: Издательско-торговая корпорация «Дашков и К°», 2012 г. - 452 с. http://ibooks.ru/
4. Савельев И. В. Курс общей физики: в 4 т.: учеб. пособие для вузов. / И. В. Савельев. - М.: КноРус, 2009.
б) дополнительная литература
1. Трофимова Т. И. Сборник задач по курсу физики для втузов: учеб. пособие для вузов / Т. И. Трофимова. - 3-е изд.- М.: ОНИКС 21 век: Мир и Образование, 2003, 2005.
2. Трофимова Т.И. Физика. Справочник с примерами решения задач. - М.: Издательство Юрайт, 2010 г. - 448 с. http://ibooks.ru/
3. Зайдель А. Н. Ошибки измерений физических величин: учебное пособие / А. Н. Зайдель. - СПб: Лань, 2009.
4. Багдасарян Д. А. Сборник задач и вопросов по электричеству и магнетизму: учеб. пособие / Д. А. Багдасарян, А. А. Сабирзянов. - Екатеринбург: Изд-во УрГУ, 2007.
5. Зисман Г. А. Курс общей физики: в 3 т.: учеб. пособие для вузов. /Г. А. Зисман, О. М. Тодес. - 7-е изд., стереотип. - М.: Лань, 2007.
6. Козлов В.Ф., Маношкин Ю.В., Миллер А.Б., Петров Ю.В. и др. Курс общей физики в задачах. - М. : ФИЗМАТЛИТ, 2010 г. — 264 с. http://ibooks.ru/
7. Оселедчик Ю.С., Самойленко П.И., Точилина Т.Н. Физика. Модульный курс (для технических вузов). Учебное пособие для вузов. - М. : Издательство Юрайт, 2010 г. - 526 с. http://ibooks.ru
8. Единая научно-образовательная электронная среда (Е-НОЭС) УрТИСИ. http://aup.uisi.ru/
9. Фриш С.Э., Тиморева А.В. Курс общей физики: Учебник для вузов: В 3 т. Изд.11. Издательский Дом Лань, 2007.
10. Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике. Для инженеров и студентов вузов. Изд.8, перераб. и испр. 2007.
в) программное обеспечение
1. Физика в анимациях.
2. Открытая физика2.6, ч.1 и2.
3. Поисковые системы (yandex.ru, google.ru и др.).
Н.И.Ильиных, Пилипенко Г.И., Вандышева И.В.
ФИЗИКА (СПЕЦГЛАВЫ)
Методические указания по выполнению практических работ
для студентов очной и заочной форм обучения,
обучающихся по направлению подготовки бакалавра
11.03.02 «Инфокоммуникационные технологии и системы связи»
(профиль «Многоканальные телекоммуникационные системы»)
программа академического бакалавриата
Екатеринбург,
2015
ББК 22.3
УДК 53
Рецензент: доцент кафедры общей физики и естествознания УрГПУ, к.ф.-м.н Сабирзянов А.А.
Ильиных Н.И., Пилипенко Г.И., Вандышева И.В.
Физика (спецглавы): Методические указания по выполнению практических работ /Н.И.Ильиных, Г.И.Пилипенко, И.В.Вандышева. – Екатеринбург: УрТИСИ СибГУТИ, 2015. - 96 с.
Методические указания предназначены для студентов очной и заочной форм обучения, изучающих дисциплину «Физика (спецглавы)» и содержат теоретические сведения, необходимые для решения задач, примеры решения задач, задачи для самостоятельного решения, список необходимой литературы.
Рекомендовано НМС УрТИСИ СибГУТИ в качестве методических указаний по выполнению практических занятий для студентов очной и заочной форм обучения для направления подготовки 11.03.02 «Инфокоммуникационные технологии и системы связи» по профилю: «Многоканальные телекоммуникационные системы», программа академического бакалавриата, квалификация «Бакалавр».
ББК 22.3
УДК 53
Кафедра высшей математики и физики
ã УрТИСИ СибГУТИ, 2015
СОДЕРЖАНИЕ
| Пояснительная записка | 4 |
| Общие методические указания к решению задач | 5 |
| Практическое занятие 1 | 6 |
| Практическое занятие 2 | 16 |
| Практическое занятие 3 | 22 |
| Практическое занятие 4 | 30 |
| Практическое занятие 5 | 41 |
| Практические занятия 6-7 | 48 |
| Практические занятия 8-9 | 64 |
| Практические занятия 10-12 | 72 |
| Практические занятия 13-14 | 84 |
| Список литературы | 96 |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Цель данного учебного пособия - оказать помощь студенту в закреплении теоретических знаний курса «Физика (спецглавы)» и приобретении необходимых навыков решения задач, необходимых при выполнении домашних и контрольных работ.
При создании пособия авторы руководствовались действующей программой курса «Физика (спецглавы)», разработанной на основании требований федерального государственного образовательного стандарта высшего образования по направлению подготовки 11.03.02 «Инфокоммуникационные технологии и системы связи (уровень бакалавриата)» 2015 г.
Пособие содержит методические указания по решению задач, краткое изложение основных положений и тем курса. Приведены примеры решения наиболее типичных задач, а также задачи для самостоятельного решения.
Объем часов, отведенных на проведение каждой работы, а также ее тема указаны в таблице.
Перечень практических работ
| Перечень практических занятий | Количество часов |
| 1. Дисперсия света. Поглощение света. Эффекты Доплера и Вавилова-Черенкова. | 4 |
| 2. Тепловое излучение. Фотоны. Давление света | 4 |
| 3. Внешний фотоэффект. Эффект Комптона | 4 |
| 4. Планетарная модель атома. Строение атома водорода по Бору. Спектры излучения атомов | 4 |
| 5. Корпускулярно-волновой дуализм свойств вещества. Волны де Бройля. Соотношение неопределенностей | 4 |
| 6. Волновая функция. Уравнение Шредингера. | 2 |
| 7. Движение заряженных частиц в потенциальной «яме» с бесконечно высокими «стенками». Туннельный эффект. | 4 |
| 8. Строение атома водорода в квантовой механике. | 2 |
| 9. Принцип запрета Паули. Многоэлектронные атомы | 2 |
| 10. Элементы квантовой статистики | 4 |
| 11. Зонная структура твердых тел | 2 |
| 12. Электропроводность полупроводников. Контактные явления | 2 |
| 13. Закон радиоактивного распада. Ядерные реакции | 4 |
| 14. Фундаментальные взаимодействия. Элементарные частицы | 4 |
| ИТОГО: | 46 |
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К РЕШЕНИЮ ЗАДАЧ
При решении задач необходимо пользоваться следующей схемой:
· Внимательно прочитать условие задачи.
· Выписать столбиком все величины, входящие в условие, и выразить их в одних единицах (преимущественно в Международной системе единиц СИ).
· Если это возможно, представить условие задачи в виде четкого рисунка. Правильно сделанный рисунок – это наполовину решенная задача.
· Уяснить физическую сущность задачи, установить основные законы и формулы, на которых базируется условие задачи.
· Если при решении задачи применяется формула, полученная для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какой-нибудь физической величины, то ее следует вывести.
· Решить задачу сначала в общем виде, то есть, в буквенных обозначениях, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин
· После получения расчетной формулы для проверки ее правильности следует подставить в правую часть формулы вместо символов величин их размерности, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.
· Подставить в конечную формулу числовые значения, выраженные в единицах СИ. В виде исключения допускается выражать в любых, но одинаковых единицах числовые значения однородных величин, стоящих в числителе и знаменателе дроби и имеющих одинаковые степени.
· При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 3520 надо записать 3,52×103, вместо 0,00129 записать 1,29×10-3 и т. п.
· Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений. Как правило, окончательный ответ следует записывать с тремя значащими цифрами. Это относится и к случаю, когда результат получен с применением калькулятора.
· Решение задачи должно сопровождаться краткими, но исчерпывающими пояснениями и комментариями.
Практическое занятие 1
Дата: 2018-12-28, просмотров: 1166.