Займемся отбором факторных признаков в модель

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Сначала с вероятностью 0,95 оценим статистическую значимость каждого из имеющихся факторных признаков. Согласно таблице критическое значение критерия Стьюдента для уровня значимости α = 1 - 0,95 = 0,05 и числа степеней свободы ν =10 – 2 = 8 равно .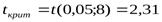

Вычислим наблюдаемые значения:

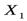: t_набл= 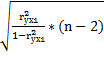= =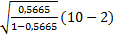2,83

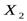: t_набл= 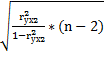= =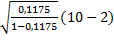1,065

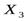: t_набл= 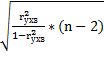= =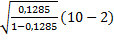1,086

Видим, что только для признака х₁>2,31 выполняется правило проверки гипотезы. Следовательно, он однозначно включается в модель.

Между признаками х₂ и х₃ нарушается принцип отсутствия автокорреляции, 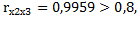связь между ними тесная. Поэтому, один из этих признаков подлежит исключению. Поскольку r_yx₃=0,3585> r_yx₂=0,3428, то признак x₂ исключается из рассмотрения, а признак x₃- остается.

Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации 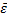, коэффициенты множественной корреляции (R) и детерминации (D).

Множественный коэффициент корреляции равен:

R_у/х1х3= 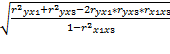= =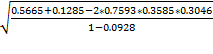0.7709

Найденное значение указывает на высокую степень тесноты и линейности корреляционной зависимости.

С вероятностью 0,95 выдвинем гипотезу о статистической значимости эмпирических данных. Поскольку n = 10, k =2, то α=1- 0,95 = 0,05, v₁=2, v₁=10-2-1. Согласно таблице F_крит=F (0.05;2;7)=4,74

Таблица 1 - Значение F-критерия Фишера при уровне значимости 0,05

v2	v1 - степени свободы (для большого среднего квадрата)
v2	1	2	3	4	5	6	7	8	9	10	11	12	14	16	20	30	40	50	100	¥
1	161	200	216	225	230	234	237	239	241	242	243	244	245	246	248	250	251	252	253	254
2	18,51	19,00	19,16	19,25	19,30	19,33	19,36	19,37	19,38	19,39	19,40	19,41	19,42	19,43	19,44	19,48	19,47	19,47	19,49	19,50
3	10,13	9,55	9,28	9,12	9,01	8,94	8,88	8,84	8,81	8,78	8,76	8,74	8,71	8,69	8,66	8,62	8,60	8,58	8,56	8,53
4	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6,00	5,96	5,93	5,91	5,87	5,84	5,80	5,74	5,71	5,70	5,66	5,63
5	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,78	4,74	4,70	4,68	4,64	4,60	4,56	4,50	4,46	4,44	4,40	4,36
6	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,10	4,06	4,03	4,00	3,96	3,92	3,87	3,81	3,77	3,75	3,71	3,67
7	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68	3,63	3,60	3,57	3,52	3,49	3,44	3,38	3,34	3,32	3,28	3,23
8	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44	3,39	3,34	3,31	3,28	3,23	3,20	3,15	3,08	3,05	3,03	2,98	2,93
9	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23	3,18	3,13	3,10	3,07	3,02	2,98	2,93	2,86	2,82	2,80	2,76	2,71
10	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07	3,02	2,97	2,94	2,91	2,86	2,82	2,77	2,70	2,67	2,64	2,59	2,54
11	4,84	3,98	3,59	3,36	3,20	3,09	3,01	2,95	2,90	2,86	2,82	2,79	2,74	2,70	2,65	2,57	2,53	2,50	2,45	2,40
12	4,75	3,88	3,49	3,26	3,11	3,00	2,92	2,85	2,80	2,76	2,72	2,69	2,64	2,60	2,54	2,46	2,42	2,40	2,35	2,30
13	4,67	3,80	3,41	3,18	3,02	2,92	2,84	2,77	2,72	2,67	2,63	2,60	2,55	2,51	2,46	2,38	2,34	2,32	2,26	2,21
14	4,60	3,74	3,34	3,11	2,96	2,85	2,77	2,70	2,65	2,60	2,56	2,53	2,48	2,44	2,39	2,31	2,27	2,24	2,19	2,13
15	4,54	3,68	3,29	3,06	2,90	2,79	2,70	2,64	2,59	2,55	2,51	2,48	2,43	2,39	2,33	2,25	2,21	2,18	2,12	2,07
16	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59	2,54	2,49	2,45	2,42	2,37	2,33	2,28	2,20	2,16	2,13	2,07	2,01
17	4,45	3,59	3,20	2,96	2,81	2,70	2,62	2,55	2,50	2,45	2,41	2,38	2,33	2,29	2,23	2,15	2,11	2,08	2,02	1,96
18	4,41	3,55	3,16	2,93	2,77	2,66	2,58	2,51	2,46	2,41	2,37	2,34	2,29	2,25	2,19	2,11	2,07	2,04	1,98	1,92
19	4,38	3,52	3,13	2,90	2,74	2,63	2,55	2,48	2,43	2,38	2,34	2,31	2,26	2,21	2,15	2,07	2,02	2,00	1,94	1,88
20	4,35	3,49	3,10	2,87	2,71	2,60	2,52	2,45	2,40	2,35	2,31	2,28	2,23	2,18	2,12	2,04	1,99	1,96	1,90	1,84
21	4,32	3,47	3,07	2,84	2,68	2,57	2,49	2,42	2,37	2,32	2,28	2,25	2,20	2,15	2,09	2,00	1,96	1,93	1,87	1,81
22	4,30	3,44	3,05	2,82	2,66	2,55	2,47	2,40	2,36	2,30	2,26	2,23	2,18	2,13	2,07	1,98	1,93	1,91	1,84	1,78
23	4,28	3,42	3,03	2,80	2,64	2,53	2,45	2,38	2,32	2,28	2,24	2,20	2,14	2,10	2,04	1,96	1,91	1,88	1,82	1,76
24	4,26	3,40	3,01	2,78	2,62	2,51	2,43	2,36	2,30	2,26	2,22	2,18	2,13	2,09	2,02	1,94	1,89	1,86	1,80	1,73
25	4,24	3,38	2,99	2,76	2,60	2,49	2,41	2,34	2,28	2,24	2,20	2,16	2,11	2,06	2,00	1,92	1,87	1,84	1,77	1,71
26	4,22	3,37	2,98	2,74	2,59	2,47	2,39	2,32	2,27	2,22	2,18	2,15	2,10	2,05	1,99	1,90	1,85	1,82	1,76	1,69
27	4,21	3,35	2,96	2,73	2,57	2,46	2,37	2,30	2,25	2,20	2,16	2,13	2,08	2,03	1,97	1,88	1,84	1,80	1,74	1,67
28	4,20	3,34	2,95	2,71	2,56	2,44	2,36	2,29	2,24	2,19	2,15	2,12	2,06	2,02	1,96	1,87	1,81	1,78	1,72	1,65
29	4,18	3,33	2,93	2,70	2,54	2,43	2,35	2,28	2,22	2,18	2,14	2,10	2,05	2,00	1,94	1,85	1,80	1,77	1,71	1,64
30	4,17	3,32	2,92	2,69	2,53	2,42	2,34	2,27	2,21	2,16	2,12	2,09	2,04	1,99	1,93	1,84	1,79	1,76	1,69	1,62
32	4,15	3,30	2,90	2,67	2,51	2,40	2,32	2,25	2,19	2,14	2,10	2,07	2,02	1,97	1,91	1,82	1,76	1,74	1,67	1,59
34	4,13	3,28	2,88	2,65	2,49	2,38	2,30	2,23	2,17	2,12	2,08	2,05	2,00	1,95	1,89	1,80	1,77	1,71	1,64	1,57
36	4,11	3,26	2,86	2,63	2,48	2,36	2,28	2,21	2,15	2,10	2,06	2,03	1,98	1,93	1,87	1,78	1,72	1,69	1,62	1,55
38	4,10	3,25	2,85	2,62	2,46	2,35	2,26	2,19	2,14	2,09	2,05	2,02	1,96	1,92	1,85	1,76	1,71	1,67	1,60	1,53
40	4,08	3,23	2,84	2,61	2,46	2,34	2,25	2,18	2,12	2,07	2,04	2,00	1,95	1,90	1,84	1,74	1,69	1,68	1,59	1,49
42	4,07	3,22	2,83	2,59	2,44	2,32	2,24	2,17	2,11	2,06	2,02	1,99	1,94	1,89	1,82	1,73	1,68	1,64	1,57	1,48
44	4,06	3,21	2,82	2,58	2,43	2,31	2,23	2,16	2,10	2,05	2,01	1,98	1,92	1,88	1,81	1,72	1,66	1,63	1,56	1,46
46	4,05	3,20	2,81	2,57	2,42	2,30	2,22	2,14	2,09	2,04	2,00	1,97	1,91	1,87	1,80	1,71	1,65	1,62	1,54	1,45
48	4,04	3,19	2,80	2,56	2,41	2,30	2,21	2,14	2,08	2,03	1,99	1,96	1,90	1,86	1,79	1,70	1,64	1,61	1,53	1,44
50	4,03	3,18	2,79	2,56	2,40	2,29	2,20	2,13	2,07	2,02	1,98	1,95	1,90	1,85	1,78	1,69	1,63	1,60	1,52	1,41
55	4,02	3,17	2,78	2,54	2,38	2,27	2,18	2,11	2,05	2,00	1,97	1,93	1,88	1,83	1,76	1,67	1,61	1,58	1,50	1,39
60	4,00	3,15	2,76	2,52	2,37	2,25	2,17	2,10	2,04	1,99	1,95	1,92	1,86	1,81	1,75	1,65	1,59	1,56	1,48	1,37
65	3,99	3,14	2,75	2,51	2,36	2,24	2,15	2,08	2,02	1,98	1,94	1,90	1,85	1,80	1,73	1,63	1,57	1,54	1,46	1,35
70	3,98	3,13	2,74	2,50	2,35	2,23	2,14	2,07	2,01	1,97	1,93	1,89	1,84	1,79	1,72	1,62	1,56	1,53	1,45	1,32
80	3,96	3,11	2,72	2,48	2,33	2,21	2,12	2,05	1,99	1,95	1,91	1,88	1,82	1,77	1,70	1,60	1,54	1,51	1,42	1,28
100	3,94	3,09	2,70	2,46	2,30	2,19	2,10	2,03	1,97	1,92	1,88	1,85	1,79	1,75	1,68	1,57	1,51	1,48	1,39	1,25
125	3,92	3,07	2,68	2,44	2,29	2,17	2,08	2,01	1,95	1,90	1,86	1,83	1,77	1,72	1,65	1,55	1,49	1,45	1,36	1,22
150	3,91	3,06	2,67	2,43	2,27	2,16	2,07	2,00	1,94	1,89	1,85	1,82	1,76	1,71	1,64	1,54	1,47	1,44	1,34	1,19
200	3,89	3,04	2,65	2,41	2,26	2,14	2,05	1,98	1,92	1,87	1,83	1,80	1,74	1,69	1,62	1,52	1,45	1,42	1,32	1,13
400	3,86	3,02	2,62	2,39	2,23	2,12	2,03	1,96	1,90	1,85	1,81	1,78	1,72	1,67	1,60	1,49	1,42	1,38	1,28	1,08
1000	3,85	3,00	2,61	2,38	2,22	2,10	2,02	1,95	1,89	1,84	1,80	1,76	1,70	1,65	1,58	1,47	1,41	1,36	1,26	1,00

При уровне вероятности Р = 0,05 и количестве степеней свободы (m— 1)/(n - m) = (3 - 1)/(10 - 3) = 2/7 оно будет составлять 4.74.

С вероятностью 0,95 выдвинем гипотезу о статистической значимости эмпирических данных. Поскольку n = 10, k =2, то α= 1- 0,95 = 0,05 v₁=2, V₂=10-2-1. Согласно таблице 10.8. F_крит=F(a;v1;v2) = F_крит=F(0,05;2;7)= 4,74

Наблюдаемое значение равно: F_набл= 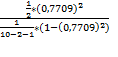=5,1275

Правило проверки гипотезы выполнено. Поэтому с вероятностью 0,95 гипотеза о статистической значимости эмпирических данных принимается, корреляционная модель может быть построена.

Общий индекс детерминации равен r= 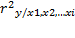=(0.7709)²=0.5943

Следовательно, факторные признаки, отобранные в модель, влияют на результативный в пределах 59,43%. Это не очень сильное влияние. Согласно закону Парето степень влияния должна быть не меньше 80%.

Дата: 2018-12-28, просмотров: 247.

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒