Двухфакторная модель мультипликативной модели
Допустим, что результативный показатель можно представить в виде произведения трех факторов: f = ху . Пролагарифмировав обе части равенства, получим
lg f=lg x+lg y
Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:
lg (f1:f0)=lg (x1:х0)+lg (y1:у0)
или lgIf= lgIx+ lgIy
Разделив обе части равенства на 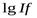 и умножив на D
и умножив на D 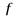 получим:
получим:
∆f= ∆f* 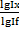 +∆f*
+∆f* 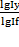 , ∆f=∆fх+∆fу.
, ∆f=∆fх+∆fу.
Отсюда влияние факторов определяется следующим образом:
∆fх= ∆f* 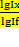 ; ∆fу=∆f*
; ∆fу=∆f* 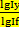 .
.
Задача 27. Используя данные таблицы 6, вычислим прирост валовой продукции за счет количества работников (КР), и среднегодовой выработки (ГВ) по факторной модели ВП =КР*ГВ:
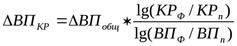 =80000
=80000 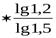 =+35 973 руб.;
=+35 973 руб.;
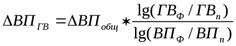 =80000
=80000 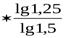 = +44 027 руб.
= +44 027 руб.
Проверка: ∆ВПобщ=∆ВПкр+∆ВПгв=35973+44027=80000 руб.
Задача 27.1 Используя данные таблицы 7, вычислим прирост валовой продукции за счет количества работников (КР), и среднегодовой выработки (ГВ) по факторной модели ВП =КР*ГВ.
При этом можно выделить из ∆fх= ∆f* 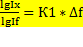 ; ∆fу=∆f*
; ∆fу=∆f* 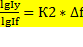 .
.
а) факторные коэффициенты К1= 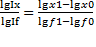 ; К2=
; К2= 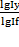 =
= 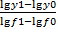
отсюда ∆f=∆f* К1+∆f*К2 или
б) общий коэффициент: ∆fх= ∆f* 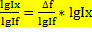 ; ∆fу=∆f*
; ∆fу=∆f* 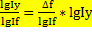 .
.
К= 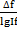 =∆f/
=∆f/ 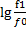 . Отсюда ∆f=К*
. Отсюда ∆f=К* 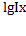 +К*
+К* 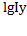 =К*ах+К*ау.
=К*ах+К*ау.
Корреляционный анализ
Пример 28. Провести корреляционный анализ зависимости выручки от числа торговых точек.
Таблица 1- Шкала Чеддока
| Теснота связи | Значение коэффициента корреляции при наличии: | |
| Прямой связи | Обратной связи | |
| Слабая | 0,1–0,3 | (–0,3)–(–0,1) |
| Умеренная | 0,3–0,5 | (–0,5)–(–0,3) |
| Заметная | 0,5–0,7 | (–0,7)–(–0,5) |
| Высокая | 0,7–0,9 | (–0,9)–(–0,7) |
| Очень высокая | 0,9–1 | (–1)–(–0,9) |
Таблица 2-Исходные данные для корреляционного анализа
| № | Число торговых точек (X) | Выручка (Y) | XY | (xi-  )2 )2
| (yi- 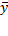 )2 )2
|
| 1. | 2 | 1598 | 3196 | 7,84 | 2291792,3 |
| 2. | 5 | 2644 | 13220 | 0,04 | 218899,2 |
| 3. | 4 | 2197 | 8788 | 0,64 | 836981,0 |
| 4. | 5 | 1959 | 9795 | 0,04 | 1329101,6 |
| 5. | 3 | 1052 | 3156 | 3,24 | 4243050,7 |
| 6. | 3 | 1922 | 5766 | 3,24 | 1415782,7 |
| 7. | 5 | 2385 | 11925 | 0,04 | 528335,2 |
| 8. | 5 | 2581 | 12905 | 0,04 | 281819,4 |
| 9. | 5 | 3105 | 15525 | 0,04 | 47,2 |
| 10. | 4 | 3896 | 15584 | 0,64 | 614865,1 |
| 11. | 4 | 1510 | 6040 | 0,64 | 2565976,8 |
| 12. | 2 | 1880 | 3760 | 7,84 | 1517495,5 |
| 13. | 5 | 3620 | 18100 | 0,04 | 258199,5 |
| 14. | 6 | 5002 | 30012 | 1,44 | 3572604,0 |
| 15. | 5 | 2819 | 14095 | 0,04 | 85770,9 |
| 16. | 4 | 4076 | 16304 | 0,64 | 929553,1 |
| 17. | 6 | 1869 | 11214 | 1,44 | 1544717,6 |
| 18. | 3 | 3524 | 10572 | 3,24 | 169853,9 |
| 19. | 6 | 3925 | 23550 | 1,44 | 661185,8 |
| 20. | 4 | 1998 | 7992 | 0,64 | 1240699,0 |
| 21. | 3 | 2606 | 7818 | 3,24 | 255901,1 |
| 22. | 5 | 2353 | 11765 | 0,04 | 575878,6 |
| 23. | 3 | 2981 | 8943 | 3,24 | 17126,1 |
| 24. | 7 | 4471 | 31297 | 4,84 | 1847243,4 |
| 25. | 6 | 2308 | 13848 | 1,44 | 646201,6 |
| 26. | 5 | 4563 | 22815 | 0,04 | 2105788,0 |
| 27. | 7 | 4306 | 30142 | 4,84 | 1425954,4 |
| 28. | 5 | 2541 | 12705 | 0,04 | 325888,8 |
| 29. | 8 | 6184 | 49472 | 10,24 | 9438003,2 |
| 30. | 9 | 7481 | 67329 | 17,64 | 19089326,1 |
| Итого: | 144 | 93356 | 497633 | 78,8 | 60034041,5 |
Решение.
Среднее число торговых точек равно: 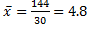
Средняя выручка: 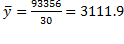 :
: 
Средний показатель ху: 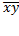 =
= 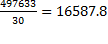
Дисперсия количества торговых точек:σ2x= 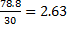
а среднеквадратическое отклонение: σx= 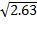 =1.62
=1.62
Дисперсия выручки:, σ2y= 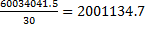
среднеквадратическое отклонение: σy= 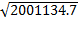 =1414.6
=1414.6
Коэффициент корреляции r = 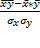 равен:
равен:
r=(16587,8-4,8*3111,9)/(1,62*1414,6)=0,72-связь высокая. Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. При этом выдвигается и проверяется нулевая гипотеза (Н0) о равенстве коэффициента корреляции нулю [Н0: r=0] При проверке этой гипотезы используется t-статистика.
tр= 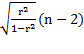 , tр - t-критерий Стьюдента.
, tр - t-критерий Стьюдента.
tр= 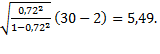 Если расчетное значение tр >tкр, то гипотеза Н0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и У.
Если расчетное значение tр >tкр, то гипотеза Н0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и У.
Дата: 2018-12-28, просмотров: 445.