Линейная модель, описывающая корреляционную зависимость, имеет следующий общий вид:
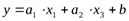 .
.
Линейная модель, описывающая корреляционную зависимость, имеет следующий общий вид: у=а1*х1+ а2*х3+ b
Используя данные таблиц, получаем систему нормальных уравнений:
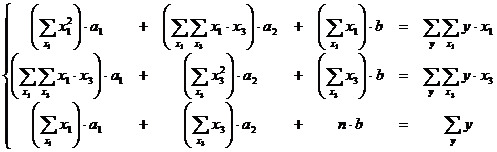 ;
;
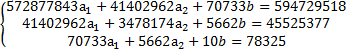
Найдем параметры уравнения регрессии упрощенным способом:
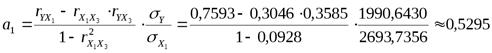
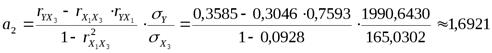 ,
,
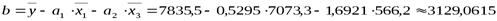 .
.
Решая систему, получаем:
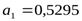 ,
, 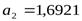 ,
, 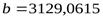 .
.
Итак, искомое уравнение регрессии имеет вид:
Yх=0,5295х1+1,6921х3+3129,0615
Оценка деятельности предприятия по использованию имеющихся возможностей проводится сравнением фактической величины результативного показателя с теоретической (расчетной), которая определяется на основе уравнения множественной регрессии. В нашем примере на предприятии №1 выпуск продукции (х1) составляет 5349 тыс. руб., численность рабочих (х3) – 331 чел. Отсюда расчетная величина основных фондов составит:
Yх=0,5295х1+1,6921х2+3129,0615=6521,4421тыс.руб.
Она превышает фактическую на 6521,4421/4999= 30,455 %. Это говорит о том, что данное предприятие использует свои возможности несколько хуже, чем в среднем все исследуемые предприятия.
Таблица 2- Расчет влияния факторов на прирост уровня выпуска продукции
| Показатели | Уровень показателя | ∆хi | bi | ∆yxi | |
| план | факт | ||||
| х1 | 5000 | 5349 | 349 | 0,5295 | 184,8 |
| х3 | 345 | 331 | -14 | 1,6921 | -23,7 |
| у | 4675 | 4999 | - | 161,1 | |
Влияние каждого фактора на прирост (отклонение от плана) результативного показателя рассчитывается следующим образом:
∆Yxi=bi*∆xi
В связи с тем что план был выполнен по фактору х1, не выполнен по фактору х3, объем выпуска продукции вырос на 161,1 тыс. руб.
Результаты многофакторного регрессионного анализа могут быть также использованы для планирования и прогнозирования уровня результативного показателя. С этой целью необходимо в полученное уравнение связи подставить плановый (прогнозный) уровень факторных показателей.
Yх=0,5295х1+1,6921х3+3129,0615
Yпл=3129,0615+0,5295*5600+1,6921*350=6686,4965 тыс. руб.
Так определяют резервы при условии прямолинейной зависимости, когда она отражается уравнением прямой.
Найдем среднюю ошибку аппроксимации. Для этого, подставив значения факторных признаков, соответствующих данному значению y в модель, получаем теоретические значения yх, yх=0,5295*5349+1,6921*331+ 3129,0615 =521,4421. Вычисления производим в таблице 10.12.
Таблица 3 - расчет исходных данных для определения средней ошибки аппроксимации
| У | х1 | х3 | Уx | У- Уx | 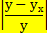
|
| 4999 | 5349 | 331 | 6521,4421 | -1522,442 | 0,30454933 |
| 6929 | 6882 | 486 | 7595,4411 | -666,4411 | 0,096181426 |
| 6902 | 7046 | 498 | 7702,5843 | -800,5843 | 0,115993089 |
| 10097 | 7248 | 789 | 8301,9444 | 1795,0556 | 0,177781083 |
| 8097 | 5256 | 359 | 6519,5774 | 1577,4226 | 0,194815685 |
| 11116 | 14090 | 724 | 11814,797 | -698,7969 | 0,062864061 |
| 4880 | 3525 | 821 | 6384,7631 | -1504,763 | 0,308353094 |
| 7355 | 5431 | 428 | 6728,9948 | 626,0052 | 0,085112876 |
| 10066 | 7680 | 607 | 8222,7262 | 1843,2738 | 0,183118796 |
| 7884 | 8226 | 619 | 8532,1384 | -648,1384 | 0,082209335 |
| Итого | - | - | - | -1522,442 | 1,610978775 |
Ошибка аппроксимации. Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Итак, значение средней ошибки аппроксимации равно:
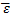 =
= 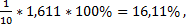 что говорит о низкой точности модели. Поскольку ошибка выше 15%, то данное уравнение можно использовать в качестве регрессии.
что говорит о низкой точности модели. Поскольку ошибка выше 15%, то данное уравнение можно использовать в качестве регрессии.
Определим значения дельта – коэффициентов. Имеем:
∆1= 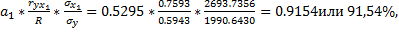
∆3= 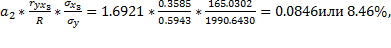
Сумма дельта – коэффициентов равна 1, следовательно, есть все основания полагать, что вычисления произведены верно. Итак, признак x1 влияет на признак Y в пределах 91,54%, а степень влияния признака x3 равна 8,46%.
Найдем величины средних коэффициентов эластичности:
e1= a1 * 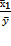 =0.5295*
=0.5295* 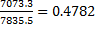 или 47,82%,
или 47,82%,
e3= a2 * 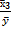 =1.6921*
=1.6921* 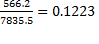 или 12,23%.
или 12,23%.
Таким образом, изменение признака x1 на 1% влечет за собой изменение признака Y на 47,82%, а вследствие изменения признака x3, изменение признака Y составит 12,23%
Перейдем к модели с парной регрессией. Поскольку одновременно минимум дельта – коэффициента и среднего коэффициента эластичности соответствует признаку x3,
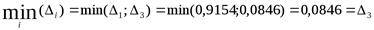 ,
,
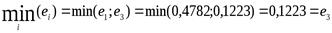 ,
,
то он исключается из модели. Итак, общий вид уравнения парной регрессии следующий:
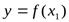 .
.
Так как rух1=0,7593>0.7, то согласно выводам задачи связь признается линейной и тесной. Уравнение прямой линии регрессии найдем упрощенным способом: 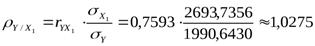 ;
;
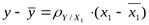 ;
;
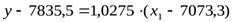 ;
;
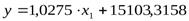 .
.
Следовательно, данное уравнение можно использовать для практических целей:
а) оценки результатов хозяйственной деятельности;
б) расчета влияния факторов на прирост результативного показателя;
в) подсчета резервов повышения уровня исследуемого показателя;
г) планирования и прогнозирования его величины.
Пример 29.1 Вначале, запишем эмпирические данные (объем выборки n=10) в виде таблицы.
Приняв стоимость основных промышленно – производственных основных фондов за результативный признак, а остальные показатели – за факторные признаки, необходимо:
а) исключив один из факторных признаков, перейти к двухфакторной регрессии;
б) вычислить множественный коэффициент корреляции и сделать выводы о форме и силе корреляционной зависимости;
в) с помощью F – критерия Фишера с вероятностью 0,95 оценить статистическую значимость эмпирических данных;
г) вычислить значение общего индекса детерминации;
д) двумя способами получить уравнение линейной модели множественной регрессии;
е) по величине средней ошибки аппроксимации оценить точность линейной модели;
ж) подсчитать дельта – коэффициенты;
з) найти значения коэффициентов эластичности;
и) исключить из модели один из факторных признаков и перейти к модели с парной регрессией;
к) провести оценку деятельности предприятия №2 на основе уравнения множественной регрессии, если плановые валовая продукция в оптовых ценах предприятия составляет 6600 тыс. руб., среднесписочная численность рабочих -490 чел., стоимость основных фондов-6700 тыс. руб., а возможный уровень этих показателей: валовая продукция в оптовых ценах предприятия - 7500 тыс. руб., среднесписочная численность рабочих -495 чел. и сделайте прогноз уровня результативного показателя.
Таблица 1 - Исходные данные для множественного корреляционного анализа
| Номер предприятия | Стоимость промышленно-производственных основных фондов,Y тыс. руб. | Валовая продукция в оптовых ценах предприятия, Х1тыс. руб. | Среднесписочная численность промышленно– производственного персонала, Х2чел. | Среднесписочная численность рабочих, Х3,чел. |
| 1 | 5000 | 5355 | 419 | 328 |
| 2 | 6890 | 6879 | 555 | 481 |
| 3 | 6910 | 7036 | 568 | 492 |
| 4 | 10012 | 7257 | 886 | 794 |
| 5 | 8082 | 5244 | 437 | 362 |
| 6 | 11115 | 14074 | 832 | 720 |
| 7 | 4877 | 3512 | 930 | 818 |
| 8 | 7344 | 5429 | 529 | 431 |
| 9 | 10022 | 7674 | 677 | 589 |
| 10 | 7899 | 8203 | 681 | 624 |
Регрессионный анализ .
Дата: 2018-12-28, просмотров: 459.