Таблица 4.9 Виды и порядок расчета средних величин
| Вид средней величины | Формула расчета |
| Среднеарифметическая простая | 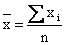 где хi – варианты показателей; n – число вариантов где хi – варианты показателей; n – число вариантов
|
| Среднеарифметическая взвешенная | 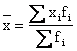 ,где fi – численность каждого варианта ,где fi – численность каждого варианта
|
| Средняя геометрическая | 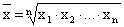
|
| Средняя хронологическая | 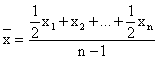
|
Для выполнения первого задания необходимо повторить темы по теории статистики “Абсолютные и относительные статистические величины. Средние величины”.
При решении задач по исчислению средних величин важно сделать правильный выбор вида и формы средней.
Пример 5. Определить среднюю заработную плату рабочих предприятия за месяц, если месячный фонд оплаты труда составляет 523 тыс. руб., среднесписочная численность работников предприятия за анализируемый период – 84 чел.
Алгоритм решения
а) Определяем среднюю величину по формуле
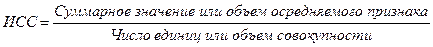
Числитель исходного соотношения средней представляет собой ее определяющий показатель. Для средней заработной платы таким определяющим показатель является фонд оплаты труда.
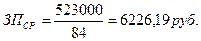
б) Вывод: средняя заработная плата работника анализируемого предприятия за месяц составила 6226 рублей 19 копеек
Задача 5.1. Определить среднюю заработную плату рабочих предприятия за месяц, если месячный фонд оплаты труда составляет 8256 тыс. руб., среднесписочная численность работников предприятия за анализируемый период – 19 чел.
Пример 6. Рассчитать среднегодовую величину активов предприятия, если стоимость активов на начало года составляла 1352 тыс. руб., а на конец года 1389 тыс. руб.
Алгоритм решения
а) Определяем среднегодовую стоимость активов предприятия по формуле средней арифметической:
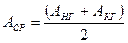 , где
, где
Анг и Акг – стоимость активов на начало и конец года соответственно
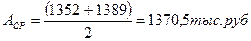
б) Вывод: среднегодовая стоимость активов предприятия составляет 1370, 5 тыс. руб.
Пример 6.1 Рассчитать среднегодовую величину активов предприятия, если стоимость активов на начало года составляла 8259 тыс. руб., а на конец года 7964 тыс. руб.
При прямой связи между признаками расчет производится по формуле средней арифметической взвешенной:
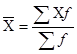 , где
, где 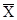 – средняя величина; X– значение признака (варианта); f– веса.
– средняя величина; X– значение признака (варианта); f– веса.
Задача 7 . Известны среднемесячная заработная плата рабочих (X) и среднемесячная численность (f), то для определения средней заработной платы нужно использовать формулу средней арифметической взвешенной. Если связь между признаками обратная, то есть известны значения одного признака (X) и объем значений (М=X*f), расчет следует производить по формуле средней гармонической взвешенной:
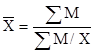 ,
,
где М– объем значений;
X– значения признака (варианта).
Пример 3 - Имеются данные о заработной плате на предприятии
| № цеха | 1 год | 2 год | ||
| Cредняя з/плата 1 рабочего за месяц (руб.) | Среднее списочное число рабочих (чел.) | Средняя з/плата 1 рабочего за месяц (руб.) | Фонд з/платы (тыс. руб.) | |
| X | F | X | M | |
| 1 | 4500 | 100 | 4700 | 376,0 |
| 2 | 4800 | 150 | 5200 | 624,0 |
Требуется:
определить среднемесячную заработную плату рабочего за каждый год, рассчитать изменения среднемесячной заработной платы (в сумме и в процентах).
Решение:
1. Среднемесячную заработную плату рабочего за 1год определяем по формуле средней арифметической взвешенной:
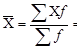
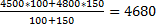 руб.
руб.
2. Среднемесячную заработную плату рабочего за 2 год определяем по формуле средней гармонической взвешенной:
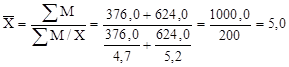 тыс. руб.
тыс. руб.
3. Изменение средней заработной платы за год составило:
5000-4680 = 320 (руб.)– рост средней заработной платы в абсолютном выражении.
5000/4680*100=106,84%
В процентах рост средней заработной платы составил + 6,84%
Задача 7.1
Имеются данные о заработной плате на предприятии:
| №цеха | 1год | 2 год | ||
| Средняя з/плата 1 рабочего за месяц (руб.) | Среднее списочное число рабочих (чел.) | Средняя з/плата 1 рабочего за месяц (руб.) | Фонд з/платы (тыс. руб) | |
| X | F | X | M | |
| 1 | 3020 | 110 | 3250 | 390,0 |
| 2 | 3240 | 140 | 3570 | 535,5 |
Требуется.
Определить среднемесячную заработную плату рабочего за каждый год, рассчитать изменения среднемесячной заработной платы (в сумме и в процентах). Указать виды средних величин, принятых в расчетах. Результаты расчетов показать в таблице и сделать экономические выводы.
Пример 9. По следующим данным вычислить среднемесячные остатки материалов за полугодие (табл.1):
Исходные данные
| Дата | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 | 1.07 |
| Остатки на начало месяца, тыс.руб. | 464.8 | 446.0 | 428.0 | 436.0 | 423.8 | 421.4 | 410.2 |
Решение. В нашей задаче даны остатки материалов на определенные моменты в ремени (1/1, 1/2, и т.д.), промежутки между которыми равны. В этом случае средняя исчисляется по формуле средней хронологического ряда:
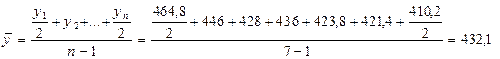 , тыс.руб.
, тыс.руб.
Пример 9.1 По следующим данным вычислить среднемесячные остатки материалов за полугодие (табл.1):
Исходные данные
| Дата | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 | 1.07 |
| Остатки на начало месяца, тыс.руб. | 1284 | 1375 | 1299 | 1471 | 1388 | 1394 | 1671 |
Относительные величины
Дата: 2018-12-28, просмотров: 589.