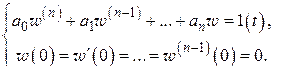Определение 2.6. Пусть функции  ,
,  удовлетворяют требованиям 10–30 в определении оригинала. Сверткой функций
удовлетворяют требованиям 10–30 в определении оригинала. Сверткой функций  ,
, 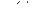 называется третья функция, вычисляемая по формуле
называется третья функция, вычисляемая по формуле
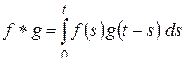 . (2.18)
. (2.18)
Например,
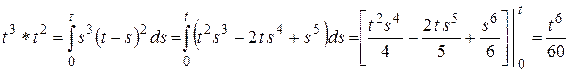 .
.
Нетрудно убедиться, что функция (2.18) также удовлетворяет требованиям
10–30.
Лемма 2.3. Имеет место равенство
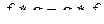 .
.
Доказательство. Выполняя в (2.18) замену переменной интегрирования: 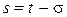 , получим
, получим
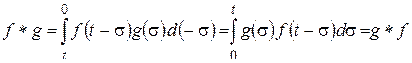 .
.
В приложениях операционного исчисления важную роль играет
Теорема 2.2. L -изображение свертки двух оригиналов равно произведению их L -изображений:
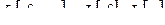 . (2.19)
. (2.19)
Доказательство. Обозначим 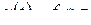 . Далее равенство (2.19) доказывается при p в полуплоскости
. Далее равенство (2.19) доказывается при p в полуплоскости  , где vk – показатели роста функций
, где vk – показатели роста функций  ,
, 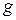 , тогда рассматриваемые несобственные интегралы сходятся (лемма 2.1) и проводимые преобразования корректны; затем оно может быть аналитически продолжено в p-плоскость. По определению (2.1) преобразования Лапласа имеем
, тогда рассматриваемые несобственные интегралы сходятся (лемма 2.1) и проводимые преобразования корректны; затем оно может быть аналитически продолжено в p-плоскость. По определению (2.1) преобразования Лапласа имеем
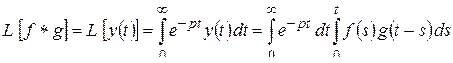 .
.
Обозначим D область на 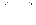 -плоскости, изображенную на рис. 2.11 (для наглядности
-плоскости, изображенную на рис. 2.11 (для наглядности 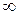 изображена точкой на числовой оси). По правилу преобразования двойного интеграла в повторный, примененному справа налево, получим
изображена точкой на числовой оси). По правилу преобразования двойного интеграла в повторный, примененному справа налево, получим
 Рис. 2.11. Рис. 2.11.
|
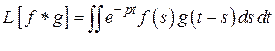 .
.
Подставим 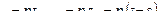 и перейдем к повторному интегралу в другом порядке:
и перейдем к повторному интегралу в другом порядке:
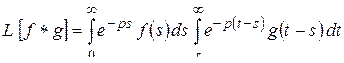 .
.
Выполняя во втором интеграле замену 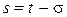 , получим
, получим
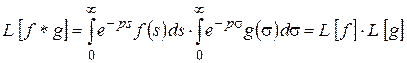 .
.
Теорема доказана.
Задание для самостоятельной работы.
Вычислить свертку следующих функций:
а)  ; б)
; б) 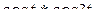 ; в)
; в) 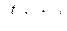 ;
;
г) 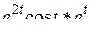 ; д)
; д) 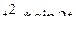 ; е)
; е) 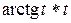 .
.
ФОРМУЛА ДЮАМЕЛЯ
В § 2.7 было установлено удобное правило описания линейных стационарных цепей на языке L-изображений с помощью передаточной функции – формулы (2.11), (2.12). Укажем часто применяемый способ описания цепей этого класса на языке оригиналов с использованием понятия «свертка». Для большей наглядности и для упрощения записей рассмотрим частный случай цепи (2.10):
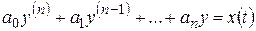 . (2.20)
. (2.20)
Выходной сигнал 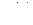 вычисляется по входному сигналу
вычисляется по входному сигналу 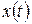 как решение задачи Коши для дифференциального уравнения (2.20) при нулевых начальных условиях:
как решение задачи Коши для дифференциального уравнения (2.20) при нулевых начальных условиях:
 .
.
Полученное далее правило остается верным для цепей общего вида (2.10).
|
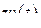 реакцию цепи (2.20) на сигнал
реакцию цепи (2.20) на сигнал 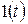 (рис. 2.12). Это означает, что
(рис. 2.12). Это означает, что 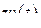 – решение задачи Коши
– решение задачи Коши

|
(2.21)
Теорема 2.3. Реакция 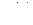 линейной стационарной цепи (2.20) на входное воздействие
линейной стационарной цепи (2.20) на входное воздействие 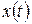 дается формулой
дается формулой
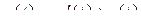 , (2.22)
, (2.22)
где 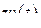 – функция (2.21).
– функция (2.21).
Доказательство. Достаточно проверить справедливость для функции (2.22) равенства  , где
, где 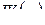 – передаточная функция цепи (2.20). Из определения функции
– передаточная функция цепи (2.20). Из определения функции 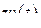 следует:
следует:
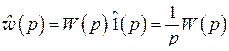 .
.
Применяя к обеим частям равенства (2.22) операцию L, с учетом теоремы о свертке (2.19), формулы для L-изображения производной и требования 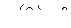 получим:
получим:
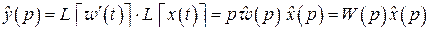 .
.
Теорема доказана.
Формула (2.22) называется формулой Дюамеля. Функция 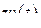 называется переходной функцией линейной стационарной цепи (2.20).
называется переходной функцией линейной стационарной цепи (2.20).
Пример. Найти переходную функцию линейной стационарной цепи
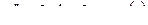 .
.
Пользуясь формулой Дюамеля, найти реакцию цепи на гармонику  .
.
Решение. Переходная функция 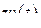 есть решение задачи Коши вида (2.21):
есть решение задачи Коши вида (2.21):
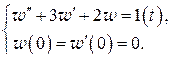
Применяя к обеим частям уравнения операцию L, вычисляя затем с учетом формулы 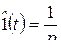 L-изображение
L-изображение 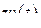 и разлагая полученную рациональную дробь в сумму элементарных дробей, получим
и разлагая полученную рациональную дробь в сумму элементарных дробей, получим
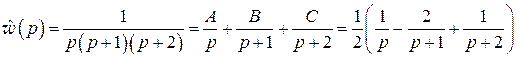 ,
,
откуда по правилу восстановления оригинала по L-изображению
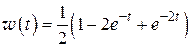 .
.
В силу теоремы 2.3 для вычисления реакции цепи на входной сигнал  нужно «свернуть» его с производной
нужно «свернуть» его с производной 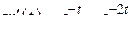 по формулам (2.22), (2.18):
по формулам (2.22), (2.18):
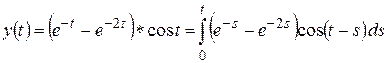 .
.
Вычисление этого интеграла с использованием приема «возвратного» интегрирования дает искомый результат:
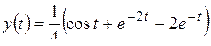 .
.
Задание для самостоятельной работы.
Найти переходные функции линейных стационарных цепей:
а) 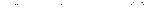 ; б)
; б) 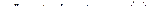 ; в)
; в) 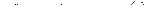 .
.
Пользуясь формулой Дюамеля, найти реакции этих цепей на сигналы 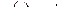 ,
, 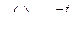 .
.
§ 2.10. ДЕЛЬТА-ФУНКЦИЯ.
ФИЛЬТРУЮЩЕЕ СВОЙСТВО ДЕЛЬТА-ФУНКЦИИ
В заключение изложим кратко широко применяемый в расчетах прием, предложенный в начале прошлого века английским физиком Дираком.
Определение 2.7. Дельта-функцией называется производная функции Хевисайда:
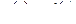 . (2.23)
. (2.23)
Из определения следует:
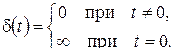
(при 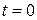 «касательная» к графику функции
«касательная» к графику функции 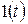 – см. рис. 2.3 – направлена вертикально, поэтому ее угловой коэффициент
– см. рис. 2.3 – направлена вертикально, поэтому ее угловой коэффициент 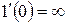 ). Очевидно,
). Очевидно, 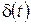 не является функцией в обычном смысле; в современной терминологии является обобщенной функцией или распределением (см. книгу [14]). В основе приложений дельта-функции лежит правило, называемое ее фильтрующим свойством. Мы приведем это правило с кратким пояснением и укажем приложение к теории автоматического управления.
не является функцией в обычном смысле; в современной терминологии является обобщенной функцией или распределением (см. книгу [14]). В основе приложений дельта-функции лежит правило, называемое ее фильтрующим свойством. Мы приведем это правило с кратким пояснением и укажем приложение к теории автоматического управления.

|
Из (2.23) следует (см. рис. 2.13): при любом 
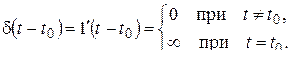 (2.24)
(2.24)
Точка  называется носителем функции
называется носителем функции 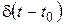 .
.
Теорема 2.4. Для любой непрерывной на оси функции 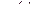 и любой
и любой 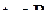 верно равенство
верно равенство
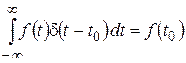 . (2.25)
. (2.25)
Таким образом, дельта-функция с носителем  «отбирает» из всех значений функции значение в точке
«отбирает» из всех значений функции значение в точке  – фильтрует множество значений.
– фильтрует множество значений.
Приведем нестрогое пояснение. Формальные вычисления по формуле (2.24) дают:
при 
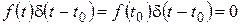 ,
,
при 
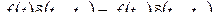 .
.
Поэтому
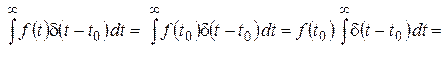
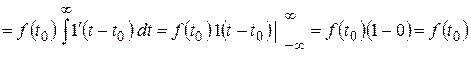 .
.
Следствие. L-изображение функции 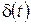 равно 1:
равно 1:
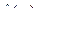 . (2.26)
. (2.26)
В самом деле, из определения (2.1) преобразования Лапласа с учетом 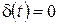 при
при 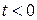 и фильтрующего свойства (2.25) получаем:
и фильтрующего свойства (2.25) получаем:
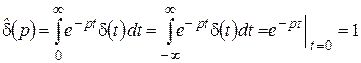 .
.

|
Рассмотрим линейную стационарную цепь с передаточной функцией 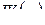 . Обозначим
. Обозначим 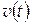 реакцию цепи на входной сигнал
реакцию цепи на входной сигнал 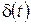 (рис. 2.14). Функция
(рис. 2.14). Функция 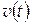 называется весовой функцией линейной стационарной цепи.
называется весовой функцией линейной стационарной цепи.
Лемма 2.4. Передаточная и весовая функции линейной стационарной цепи связаны соотношением
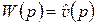 . (2.27)
. (2.27)
Доказательство. По формулам (2.11), (2.26) имеем:
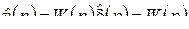 .
.
Теорема 2.5. Реакция 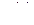 линейной стационарной цепи (2.10) с весовой функцией
линейной стационарной цепи (2.10) с весовой функцией 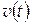 на входное воздействие
на входное воздействие 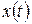 дается формулой
дается формулой
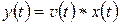 . (2.28)
. (2.28)
Доказательство. По формулам (2.19), (2.27) получаем:
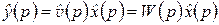 ,
,
откуда следует требуемое.
Пример. Решить пример из § 2.9, пользуясь понятием весовой функции и теоремой 2.5.
Решение. Весовая функция 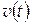 есть решение задачи Коши
есть решение задачи Коши
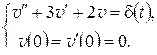
Применяя к обеим частям уравнения операцию L и используя формулу (2.26) для L-изображения дельта-функции: 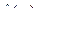 , после простых вычислений
, после простых вычислений
найдем:
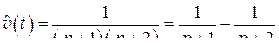 ,
,
откуда
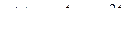 .
.
По формуле (2.28) получаем, как и в § 2.9:
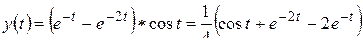 .
.
Задание для самостоятельной работы.
Решить примеры а), б), в), указанные в конце § 2.9, пользуясь понятием весовой функции и теоремой 2.5.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Маркушевич А.И. Введение в теорию аналитических функций /
А.И. Маркушевич, Л.А. Маркушевич. – М.: Просвещение, 1977.
2. Шабат Б.В. Введение в комплексный анализ / Б.В. Шабат. – М.: Наука, 1976. – Ч. 1.
3. Поддубный Г.В. Математический анализ для радиоинженеров /
Г.В. Поддубный, Р.К. Романовский. – М.: Воениздат, 1976.
4. Краснов М.Л. Функции комплексного переменного. Операционное исчисление. Теория устойчивости / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. – М.: Наука, 1971.
5. Мышкис А. Д. математика для втузов (специальные курсы) /
А.Д. Мышкис. – М.: Наука, 1971.
6. Лебедев Н.Н. Специальные функции и их приложения / Н.Н. Лебедев. – М.: ГИТТЛ, 1953.
7. Диткин В.А. Введение в комплексный анализ / В.А. Диткин,
А.П. Прудников. – М.: ГИФМЛ, 1961.
8. Мартыненко В.С. Операционное исчисление / В.С. Мартыненко. – Киев: Высшая школа, 1973.
9. Ройтенберг Я.Н. Автоматическое управление / Я.Н. Ройтенберг. – М.: Наука, 1978.
10. Попов Е.П. Теория линейных систем автоматического регулирования и управления / Е.П. Попов. – М.: Наука, 1978.
11. Чаки Ф. Современная теория управления / Ф. Чаки. – М.: Мир, 1975.
12. Шаталов А.С. Теория автоматического управления / А.С. Шаталов. – М.: Энергия, 1977.
13. Воронов А.А. Устойчивость, управляемость, наблюдаемость /
А.А. Воронов. – М.: Наука, 1978.
14. Владимиров В.С. Уравнения математической физики / В.С. Владимиров, В.В. Жаринов. – М.: ФМЛ, 2000.
Министерство образования и науки Российской Федерации

Государственное образовательное учреждение
высшего профессионального образования
«Омский государственный технический университет»

Дата: 2018-12-28, просмотров: 979.