Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

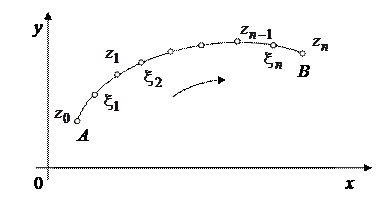
Пусть функция 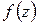 задана и непрерывна на некоторой дуге АВ[4]
(рис. 1.5). Точку А будем считать начальной, точку В – конечной точкой дуги; тем самым на дуге выбрано положительное направление.

Разделим дугу АВ произвольным образом на п частей и зану­меруем точки деления в направлении от начала к концу дуги: 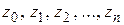 ( 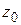отвечает началу,  – концу дуги). На каждой частичной дуге выберем точки и обозначим эти точки 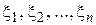 (нумерация «от начала к концу»). Составим сумму

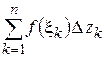,                                          (1.16)

где обозначено

 

Рис. 1.5.

Определение 1.7. Предел суммы (1.16) при стремлении к нулю длины наибольшей из частных дуг называется интегралом от функции 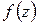 по дуге АВ и обозначается :

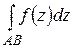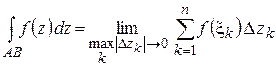.                        (1.17)

 

Из определения вытекают следующие свойства интеграла[5]:

1°.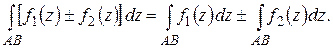

2°. 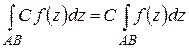 (С – постоянная).

3°.

(если точку B объявить начальной, а точку А – конечной, то все множители 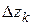 в правой части (1.17) изменят знак на противопо­ложный).

4°. Если дуга АВ разделена на части точкой С, то

.

5°. Если во всех точках дуги АВ  и длина дуги АВ равна L, то

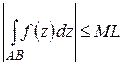.                                        (1.18)

Действительно, согласно (1.3) имеем:

.

Но 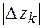 есть расстояние между точкам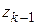и  и 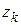 и, следова­тельно,  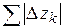есть длина ломаной линии, вписанной в дугу АВ, поэтому

.

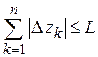Следовательно,

.

откуда в пределе получаем (1.18).

6°. 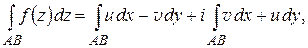                            (1.19)

где , .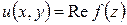

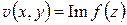Действительно, обозначая 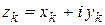, , 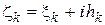получим:

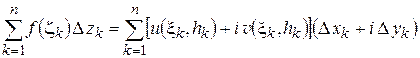
или

Суммы в правой части этого равенства являются инте­гральными суммами криволинейных интегралов второго рода 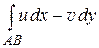, , 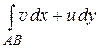поэтому предельный переход при условии  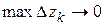или, что то же, при условиях 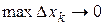,  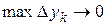дает формулу (1.19).

Замечание. Существование пределов интегральных сумм в пра­вой части последнего равенства (т. е. криволинейных интегралов в (1.19)) обеспечено непрерывностью функций 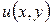,  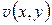на дуге АВ. Следовательно, предел интегральной суммы в левой части равенства, т. е. интеграл  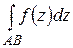существует, если функция  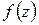непрерывна на дуге АВ.

7°. Если дуга АВ задана параметрическими уравнениями

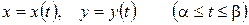
или, что то же, комплексным параметрическим уравнением

,

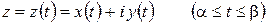то имеет место формула

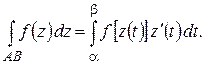                                 (1.20)

Предлагаем читателю доказать формулу (1.20) самостоятельно.

Отметим, что в частном случае конечная точка дуги АВ может совпадать с начальной, т. е. дуга может оказаться замкнутой. Интеграл по замкнутой дуге  (или, как мы будем в дальнейшем говорить, по замкнутому контуру ) обозначается

стрелка указывает направление, по которому вычис­ляется интеграл[6]. Очевидно, для интегралов по замкнутому кон­туру справедливы все свойства 1°–7°.

Рис. 1.6.

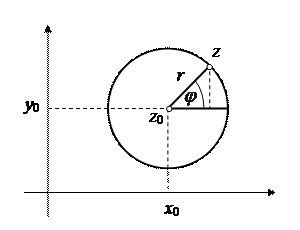
Пример 1. Вычислить , где  – окружность .

Решение. Параметрические уравнения окружности  (рис. 1.6) суть

,

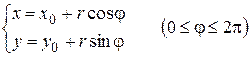или, в комплексной форме,

,

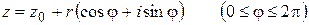поэтому, в силу (1.20),

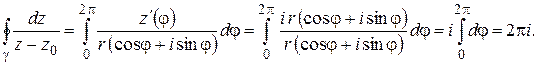
Пример 2. Вычислить 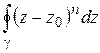, где  – окружность 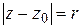, п – целое число, п .

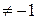Решение. Аналогично предыдущему получим:

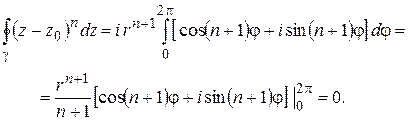
Обратим внимание, что интегралы в примерах 1, 2 не зависят от радиуса окружности :

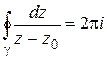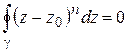,  (n – целое, 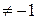).            (1.21)

Пример 3. Доказать формулу

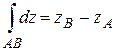,                                              (1.22)

где 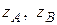 – комплексные числа, отвечающие началу и концу дуги АВ.

Решение. Имеем:

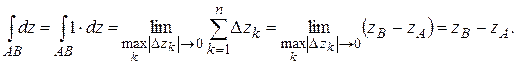
Задание для самостоятельной работы.

Вычислить .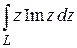

а) L – отрезок прямой, соединяющий точку 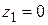 с точкой ;

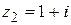б) L – ломаная, состоящая из отрезка, соединяющего точку 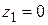 с точкой 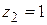, и отрезка, соединяющего точку  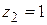с точкой ;

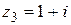в) L – окружность 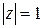, проходимая в положительном на­правлении (против часовой стрелки).

 

ТЕОРЕМА КОШИ

В этом параграфе будет установлен фундаментальный факт теории функций комплексного переменного.

Теорема 1.2. Если функция 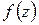 аналитична в односвязной об­ласти D, ограниченной замкнутым контуром , а также в точках этого контура, то интеграл от этой функции по контуру  равен нулю:

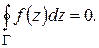
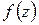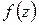Доказательство. Аналитичность функции  на контуре  означает ее дифференцируемость в малых окрестностях точек , поэтому функция  будет дифференцируемой в некоторой об­ласти D₁, содержащей целиком внутри контур  и область D (рис. 1.7). Следовательно, ее действительная и мнимая части удо­влетворяют в области D₁ условиям Коши – Римана

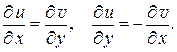
В силу (1.19) имеем:

 

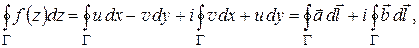
где обозначено

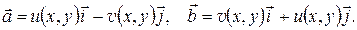
Вычислим роторы векторов :

 

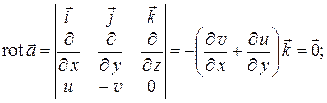
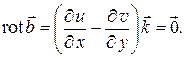
Рис. 1.7.

 

Таким образом, векторы 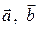 являются потенциальными в односвязной области D₁. Следовательно, циркуляция каждого из них по любому замкнутому контуру, лежащему внутри D₁ , равна нулю [7]; в частности, 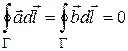, откуда

следует 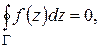 что и требовалось доказать.

Следствие. Если функция 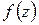 аналитична в многосвязной об­ласти D, ограниченной внешним контуром  и внутренними конту­рами  (рис. 1.8), а также в точках контуров , , то имеет место формула

                                (1.23)

В самом деле, пусть, например, внутри контура  (рис. 1.8) лежат два контура 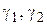 и функция  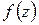аналитична в трехсвязной области между контуром  и контурами 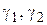, а также на всех этих контурах.

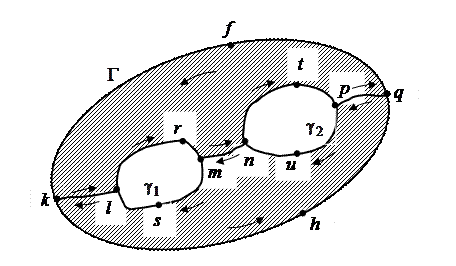
Рис. 1.8.

 

Проведем гладкие дуги kl, тп, р q, соединяющие  с ,  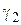с ,  с , и обозначим через  замкнутый контур 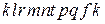, через  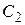– замкнутый контур 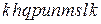. Тогда в силу теоремы Коши 1.2

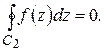
Складывая эти равенства и учитывая, что интегрирование по каждой из дуг kl, тп, р q происходит дважды в противоположных направлениях, получим:

что и требовалось.

Пусть функция 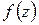 аналитична в односвязной области D. Вы­берем в области D две точки  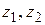и проведем две дуги 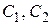, соединяющие  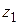с 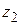 и целиком лежащие в D (рис. 1.9).

Тогда из теоремы Коши вытекает:

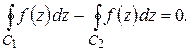
Таким образом, если функция аналитична в односвязной об­ласти, то интеграл от нее по любому лежащему в области пути, соединяющему две заданные точки области, одинаков, поэтому имеет смысл обозна­чение

Рассмотрим интеграл с переменным верхним пределом

Рис. 1.9.

 

Так как

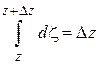
(см. формулу (1.22)), то

              (1.24)

Функция 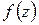 непрерывна в точке 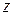, поэтому для любого  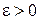найдется такое 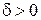, что при  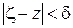будет 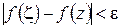. Выбирая в (1.24)  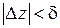и пользуясь оценкой (1.18) для модуля интеграла, получим:

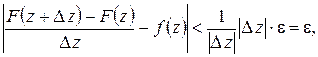
откуда следует

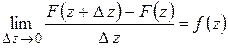       или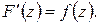       

Таким образом, доказано, что функция аналитическая в односвязной области имеет первообразную. Добавим к этому, что любые две первооб­разные аналитической функции отличаются на постоянную. В самом деле, есл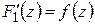и  и 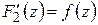, то, обозначив

,

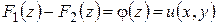получим 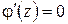 и, следовательно, согласно формуле (1.13)

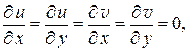
откуда

Из сказанного непосредственно вытекает формула Ньютона – Лейбница для аналитических функций:

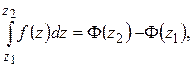
где 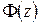 – какая-либо первообразная к .

 

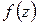Задание для самостоятельной работы.

Доказать: если – замкнутый контур, содержащий внутри точку , то

.

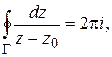
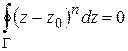
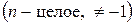Вытекает ли последнее равенство из теоремы Коши?

 

ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ

Пусть функция 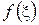 аналитична в односвязной области D, огра­ниченной замкнутым контуром , и на самом контуре. Зафикси­руем в области D точку 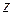 (рис. 1.10) и зададимся произвольным 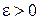. Так как  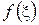непрерывна в точке 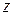, то найдется такое 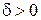, что во всех точках 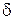-окрестности точки  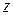выполняется неравенство

 

 

 

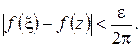
Рис. 1.10.

Проведем окружность 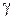 с центром в точке  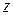радиуса 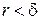. Пользуясь оценкой (1.18) для модуля интеграла, получим:

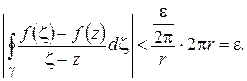
(Здесь учтено, что если 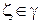, то 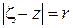). Но по следствию из теоремы Коши

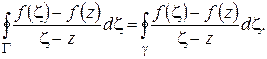
Следовательно,

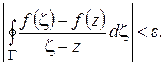
Ввиду произвольности 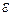отсюда следует, что

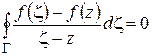
или, что то же,

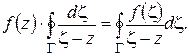
Используя полученный ранее результат (1.21) и деля почленно на 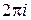, получим:

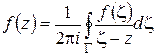.                                      (1.25)

Эта формула называется интегральной формулой Коши. Для вычисления интеграла в правой части (он называется интегралом Коши) нужно, очевидно, знать значения функции 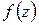 только на контуре . Таким образом, формула Коши позволяет находить значения аналитической функции внутри области, если известны ее значения на границе области.

Замечание 1. Из формулы Коши вытекает: если две функции 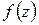,  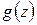аналитические внутри замкнутого контура  и на са­мом , имеют одинаковые значения в точках , то они имеют оди­наковые значения и во всех точках внутри . Это утверждение может быть обобщено следующим образом: если две функции, анатилитические в односвязной области D, имеют одинаковые зна­чения на некоторой дуге, лежащей в D, то они совпадают во всей области D. Это замечательное свойство аналитических функций называется свойством единственности.

Замечание 2. Если на дуге 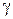 (замкнутой или незамкнутой) за­дана непрерывная функция 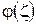, то выражение

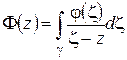                                            (1.26)

имеет смысл при 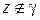 и называется интегралом типа Коши. Из (1.26) следует

.

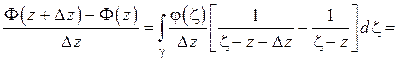
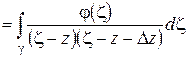Предельный переход дает

.

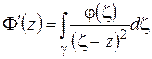Аналогично доказывается существование 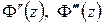 и т. д., при этом

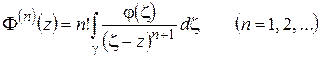.                      (1.27)

Так как интеграл Коши является частным случаем интеграла типа Коши, то из (1.25) и (1.27) вытекает: функция 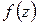, анали­тическая в области D, имеет производные всех порядков в D, при этом

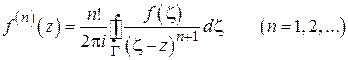,                   (1.28)

где 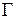– любой замкнутый контур, содержащий внутри точку z .

Доказанная формула (1.25) играет существенную роль в даль­нейших исследованиях. Сейчас мы покажем, как эта формула может быть использована для вычисления интегралов.

Пример. Вычислить , где 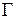– окружность .

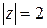Решение. Обозначим 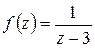, тогда

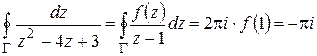
(здесь использовано, что 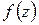 аналитична внутри и на ).

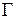Задание для самостоятельной работы.

1) Будет ли верным вычисление, проведенное в последнем при­мере, если в качестве контура 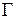 взять окружность 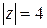? Как использовать формулу Коши для вычисления интеграла по такому контуру?

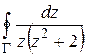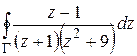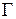2) Вычислить интегралы , , где – окружность .

 

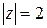СТЕПЕННЫЕ РЯДЫ

Определение 1.8. Ряд с комплексными членами

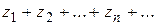                                       (1.29)

называется сходящимся к числу 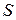, если последовательность част­ичных сумм  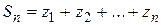имеет предел, равный 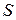, т. е. если для любого  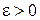найдется такой номер 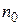, что при  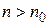выпол­няется неравенство 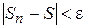. Число  называется суммой ряда.

Обозначим 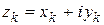 и рассмотрим ряды:

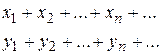                                       (1.30)

Если ряды (1.30) сходятся соответственно к 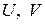 то ряд (1.29) сходится к числу 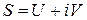. Обратно, если ряд (1.29) сходится: 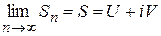, то , , 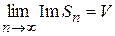т. е. ряды (1.30) сходятся. Таким образом, для сходимости ряда (1.29) с комплексными членами необходимо и достаточно, чтобы сходились ряды (1.30), составленные соответственно из действительных и мнимых частей членов этого ряда.

Отсюда, в частности, следует: если ряд с комплексными чле­нами сходится, то его общий член стремится к нулю. В самом деле, из сходимости ряда (1.29) вытекает сходимость рядов (1.30) и, следовательно, стремление 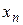,  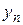к нулю, откуда следует нужное.

Определение 1.9. Если сходится ряд модулей

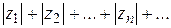,                                     (1.31)

то ряд (1.29) называется абсолютно сходящимся.

Абсолютно сходящийся ряд сходится. В самом деле, если 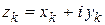, то 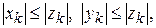 поэтому из сходимости ряда (1.31) вытекает сходимость рядов (1.30), а следовательно, и ряда (1.29).

Определения и свойства суммы, разности и произведения ря­дов с действительными членами без изменений переносятся на ряды с комплексными членами.

Рассмотрим комплексный степенной ряд

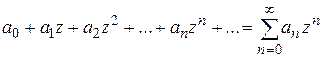                  (1.32)

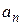( – комплексные числа, называемые коэффициентами ряда, 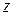– комплексное переменное).

Теорема 1.3 (теорема Абеля). Если степенной ряд (1.32) схо­дится при некотором значении переменного 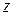, то он абсолютно сходится при всех значениях  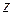с меньшим модулем.

Доказательство. Пусть сходится ряд , тогда последовательность чисел 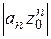 сходится к нулю и, следовательно, ограничена, т. е. найдется такое 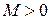, что

.

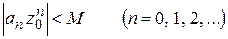Если 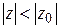, то число  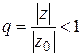и

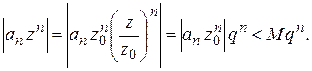
Так как геометрическая прогрессия 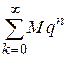 сходится, то на осно­вании теоремы сравнения для рядов с неотрицательными членами ряд  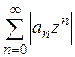сходится; следовательно, ряд  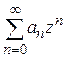абсолютно сходится, что и требовалось доказать.

Замечание. Из теоремы Абеля вытекает: если степенной ряд расходится в точке , то он расходится при . В самом деле, если бы ряд 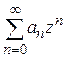 сходился, то по теореме Абеля (так как 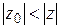) ряд 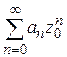 был бы сходящимся, что противоречит условию.

Содержание теоремы Абеля можно не вполне строго выразить так: точки сходимости степенного ряда расположены ближе к нулю, чем любая точка расходимости.

Теорема Абеля позволяет исследо­вать структуру области сходимости степенного ряда.

В отношении степенного ряда (1.32) возможны три случая:

1) все положительные числа яв­ляются точками сходимости;

2) все положительные числа яв­ляются точками расходимости;

3) существуют положительные точ­ки сходимости и положительные точки расходимости.

В первом случае по теореме Абеля ряд сходится во всей плоскости. Во втором случае по замечанию к теореме Абеля ряд сходится только в одной точке 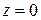. В третьем случае, так как точки сходимости расположены ближе к нулю, чем точки расходимости, найдется «пограничная» точка 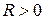, отделяющая  положительные  точки сходимости от положительных точек расходимости

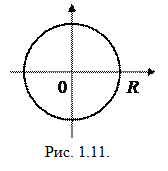
(в самой этой точке ряд может схо­диться либо расходиться). Проведем на плоскости круг радиуса 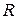 с центром в начале координат (рис. 1.11). Тогда, оче­видно, ряд (1.32) будет абсолютно сходиться внутри круга и расходиться вне круга (сходимость или расходимость на границе круга неизвестна).

Построенный круг называется кругом сходимости степенного ряда (1.32), а его радиус 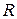 – радиусом сходимости ряда (1.32). В случаях 1), 2) можно считать соответственно 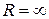, . Прак­тическое вычисление радиуса сходимости может быть выполнено с помощью известных признаков сходимости рядов.

Заметим, что ряд

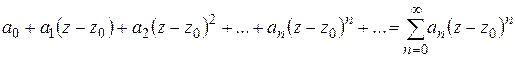,      (1.33)

где 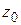 – любое комплексное число, также называется степенным рядом, его областью сходимости является круг с центром в точке .

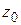Рассмотрим круг 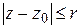, лежащий внутри круга сходи­мости ряда (1.33). Тогда числовой ряд

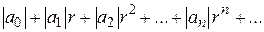
сходится и является мажорантой для ряда (1.33) в круге , это значит, что  для всех п.

Определение 1.10. Если для ряда функций

,                                   (1.34)

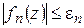
определенных на некотором множестве М, существует сходящаяся числовая мажоранта: при всех 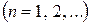, где 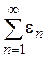– сходящийся числовой ряд, то будем говорить, что ряд (1.34) правильно сходится на множестве М.

Из сказанного выше вытекает

Лемма 1.1. Степенной ряд (1.33) правильно сходится в любом круге , лежащем внутри круга сходимости.

Нам понадобятся следующие два свойства правильно сходя­щихся рядов.

Теорема 1.4. Если члены ряда (1.34) непрерывны на дуге 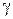 и ряд правильно сходится на 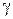, то и сумма  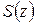ряда (1.34) непре­рывна на  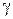и ряд можно почленно интегрировать по дуге :

 .

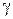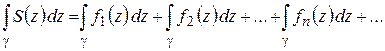Теорема 1.5. Если члены ряда (1.34) являются аналитическими функциями в области D и ряд правильно сходится в D, то и сумма 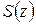 ряда (1.34) является аналитической функцией в области D и ряд (1.34) можно почленно дифференцировать в области D:

 .

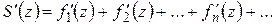Первая из этих теорем доказывается так же, как аналогичная теорема для функций действительного переменного. Для доказатель­ства второй выберем окружность 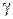, лежащую вместе с внутренно­стью в области D, и зафиксируем точку  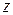внутри 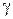. Тогда при 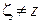справедливо тождество

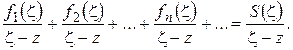                         (1.35)

Так как ряд (1.34) имеет в области D сходящуюся числовую мажоранту 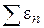, то ряд (1.35) имеет на  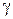сходящуюся числовую мажоранту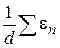  
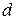( – минимальное расстояние от точек  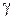до 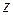), т. е. правильно сходится на 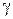. Интегрируя почленно ряд (1.35) по  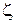и учитывая, что вследствие аналитичности функций  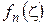внутри  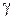и на 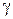 интегралы в левой части могут быть вычислены по формуле Коши (1.25), получим:

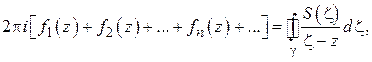
откуда находим:

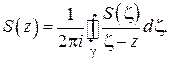
Таким образом, в точках 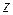, лежащих внутри 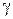, функция  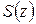представляется интегралом типа Коши; следовательно (см. § 1.8, замечание 2),  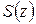является аналитической функцией внутри 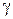. Так как каждая точка области содержится внутри некоторого круга, лежащего целиком в области, из доказанного вытекает аналитичность  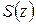в области D.

Аналогично, интегрируя почленно по контуру 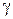 равенство

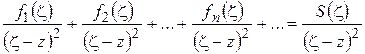
и учитывая формулу (1.28) для производных аналитической функции, получим 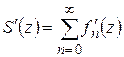, что и требовалось доказать.

Заметим, что аналогичное утверждение не имеет места для функций действительного переменного: из дифференцируемости членов правильно сходящегося ряда не вытекает дифференцируемость суммы ряда и возможность почленного дифференцирования.

Из леммы 1.1 и теорем 1.4, 1.5 вытекает

Следствие. Сумма степенного ряда (1.33) является аналитиче­ской функцией в круге сходимости; степенной ряд можно почленно дифференцировать в круге сходимости и почленно интегрировать по любой дуге, лежащей в круге сходимости.

Задание для самостоятельной работы.

Доказать, что ряд 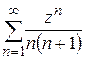 правильно сходится в круге сходимости.