В § 1.2 было отмечено, что функция комплексного переменного 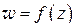 задает отображение множества М точек на z-плоскости (области определения 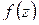) на некоторое множество N точек на 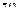-плоскости (области значений 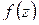). В этом параграфе будут кратко рассмотрены отображения, даваемые аналитическими функциями.

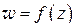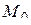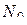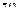В дальнейшем мы будем употреблять следующий термин. Если при отображении  множество  на z-плоскости переходит в множество  на -плоскости, то будем называть множество  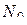образом множества  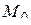при отображении .

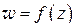Пусть функция 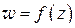 аналитична в точке 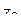, , 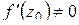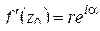. Выясним геометрический смысл чисел .

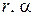Проведем через точку 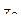 какую-нибудь кривую l, имеющую в точке  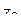касательную. Если кривая l описывается параметрическим уравнением  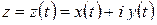и 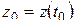, то направление касательной к l в точке  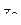дается вектором  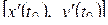или комплексным числом  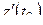(рис. 1.20, а).

Функция 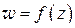 переводит кривую l в некоторую кривую  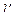на
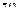-плоскости с параметрическим уравнением 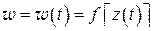, проходящую через точку  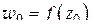(рис. 1.20, б). Направление касательной к  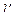в точке  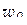дается комплексным числом 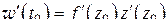. Имеем

,

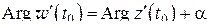отсюда следует: аргумент 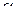 производной  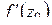равен углу, на который поворачиваются касательные ко всем кривым в точке  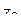при отображении 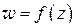. Из сказанного, в частности, вытекает: если две кривые 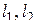, проходящие через точку 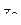, образуют между собой угол  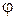(т. е. угол между касательными в точке  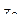равен 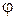), то угол между их образами  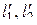на
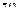-плоскости также равен  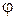(с сохранением направления отсчета) (рис. 1.21).

Рис. 1.20.

Далее имеем:

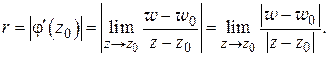                   (1.75)

Величина 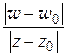 показывает, во сколько раз растягивается отрезок  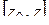при

отображении 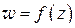. Предел этой величины при условии  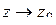естественно называть коэффициентом растяжения в точке 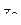: он показывает, во сколько раз растягиваются ма­лые отрезки, исходящие из точки 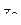. Таким образом, модуль  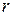производной  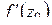равен коэффициенту растяжения в точке  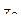при отображении 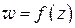. Так как предел (1.75) не зависит от направления,
по которому 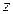 приближается к  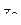(это следует из определения производной), то коэффициент растяжения одинаков по всем направлениям, исходящим из точки .

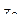Рис. 1.21.

Определение 1.12. Отображение 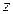-плоскости (или части 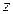-плоскости) в 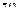-плоскость, которое

1) сохраняет углы (и направление их отсчета),

2) растягивает одинаково (в малом) по всем направлениям называется конформным отображением.

Таким образом, нами доказано, что отображение, даваемое аналитической функцией 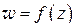 с отличной от нуля производ­ной, является конформным отображением.

Для применений в физике и технике важна следующая задача. Заданы области D, 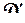 соответственно в 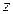-плоскости и 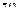-плоскости; требуется построить функцию 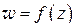, дающую конформное и взаимно однозначное отображение области D на область  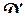(т. е. такое конформное отображение, при котором  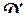является обра­зом D и при этом каждая точка  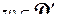является образом един­ственной точки 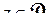). Мы рассмотрим две частных задачи такого типа: об отображении заданного круга на другой заданный круг или на полуплоскость и об отображении полуплоскости на прямо­угольник. Вначале сделаем следующее

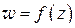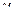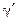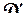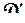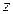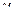Замечание. В связи с поставленной выше задачей возникает такой вопрос: пусть найдено конформное отображение , при котором граница  области D переходит в границу обла­сти ; можно ли утверждать, что при этом область D переходит в область ? Ответ на этот вопрос таков: если при перемещении точки  по  в положительном направлении относительно области D (т. е. таком, при котором область D остается слева от 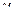) ее образ  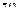перемещается по  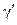в положительном направлении относительно области 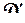, то область D переходит в  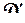(рис. 1.22). Обоснование этого правила мы не приводим (оно требует привлечения математического аппарата, выходящего за рамки пособия).

Рис. 1.22.