§ 2.1. ОРИГИНАЛ. L -ИЗОБРАЖЕНИЕ ОРИГИНАЛА
Будем рассматривать функции времени (сигналы) со свойствами
10. 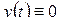 при
при 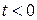 ;
;
20. 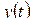 непрерывна при
непрерывна при 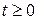 ;
;
30. 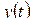 растет не быстрее экспоненты при
растет не быстрее экспоненты при  : существуют числа
: существуют числа  ,
, 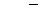 такие, что
такие, что
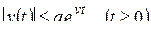 .
.
Определение 2.1. Функция со свойствами 10 – 30 называется оригиналом (рис. 2.1). Точная нижняя грань чисел 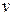 , при которых верна оценка 30, называется показателем роста оригинала
, при которых верна оценка 30, называется показателем роста оригинала 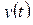 .
.

| 
|
Рис. 2.1. Рис. 2.2.
Определение 2.2. Преобразованием Лапласа или 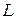 -изображением оригинала
-изображением оригинала 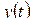 называется функция комплексного переменного
называется функция комплексного переменного 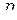 , вычисляемая по формуле
, вычисляемая по формуле
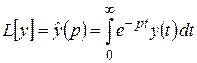 . (2.1)
. (2.1)
Поставим вопрос: при каких значениях 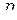 существует неопределенный интеграл (2.1)? Рассмотрим на
существует неопределенный интеграл (2.1)? Рассмотрим на 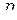 -плоскости полуплоскость
-плоскости полуплоскость 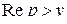 , где
, где 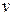 – показатель роста
– показатель роста 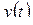 (рис. 2.2).
(рис. 2.2).
Лемма 2.1. Интеграл (2.1) сходится при всех 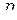 в полуплоскости
в полуплоскости 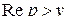 .
.
Доказательство. Воспользуемся теоремой сравнения для несобственных
интегралов: если 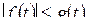 при
при 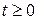 и интеграл
и интеграл 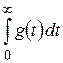 сходится, то интеграл
сходится, то интеграл
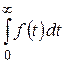 также сходится. Имеем: при
также сходится. Имеем: при 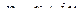
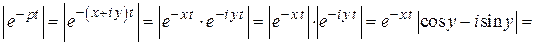
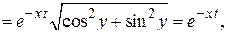
откуда с учетом свойства 30 оригинала следует оценка
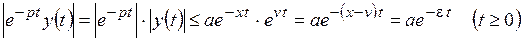 .
.
При 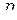 в полуплоскости
в полуплоскости 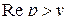 будет
будет  (рис. 2.2) и интеграл от правой части этого неравенства по промежутку
(рис. 2.2) и интеграл от правой части этого неравенства по промежутку 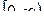 сходится (поверьте это), тем самым и подавно сходится интеграл (2.1).
сходится (поверьте это), тем самым и подавно сходится интеграл (2.1).
Лемма 2.2. Функция (2.1) является аналитической функцией в полуплоскости 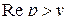 .
.
Доказательство. Мы знаем: аналитичность функции комплексного переменного 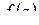 в области равносильна существованию производной первого порядка
в области равносильна существованию производной первого порядка 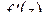 в этой области. Дифференцирование интеграла (2.1) по параметру
в этой области. Дифференцирование интеграла (2.1) по параметру 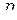 дает
дает
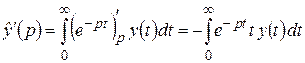 .
.
Аналогично предыдущему нетрудно убедиться, что несобственный интеграл в правой части сходится (проверьте это). Лемма доказана.
Тем самым к функции (2.1) применимы все правила теории аналитичес-ких функций, установленные в разделе 1.
Теория преобразования Лапласа называется операционным исчислением. Далее излагаются (как правило без доказательства) и иллюстрируются на примерах основные правила операционного исчисления, затем построенный математический аппарат применяется к некоторым задачам теории дифференциаль-ных уравнений и теории автоматического управления.
В заключение этого параграфа рассмотрим два простых примера на вычисление 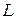 - изображений.
- изображений.
Пример 1. Найти 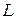 - изображение функции Хевисайда
- изображение функции Хевисайда
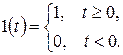
Решение. Функция 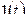 очевидным образом удовлетворяет требованиям 10 – 30 с показателем роста
очевидным образом удовлетворяет требованиям 10 – 30 с показателем роста  , тем самым является оригиналом. По лемме 2.1
, тем самым является оригиналом. По лемме 2.1
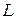 - изображение определено в полуплоскости
- изображение определено в полуплоскости 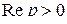 (рис. 2.4). По формуле (2.1) найдем
(рис. 2.4). По формуле (2.1) найдем
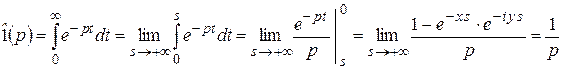 ;
;
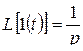 . (2.2)
. (2.2)

| 
|
Рис. 2.3. Рис. 2.4.
Пример 2. Найти 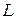 - изображение функции
- изображение функции
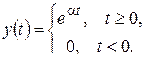
Решение. Данная функция (рис. 2.5) является оригиналом с показателем роста 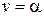 , поэтому
, поэтому 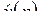 определена в полуплоскости
определена в полуплоскости 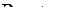 (рис. 2.6).
(рис. 2.6).
По формуле (2.1) имеем
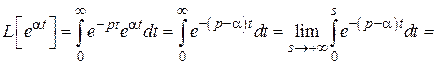
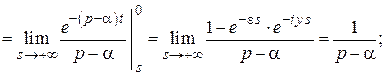
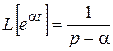 . (2.3)
. (2.3)
Отметим, что формула (2.2) формально содержится в (2.3): случай  .
.
Замечание 1. Мы вывели формулу (2.3) при условии 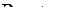 . Однако правая часть (2.3) определена при всех
. Однако правая часть (2.3) определена при всех 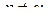 . Далее будем считать формулу (2.3) верной при всех
. Далее будем считать формулу (2.3) верной при всех 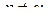 . Так же будем поступать и в других случаях: будем считать формулу для
. Так же будем поступать и в других случаях: будем считать формулу для 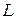 -изображения верной при всех p , при которых полученное выражение имеет смысл. Говорят так:
-изображения верной при всех p , при которых полученное выражение имеет смысл. Говорят так: 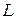 -изображение аналитически продолжается из полуплоскости
-изображение аналитически продолжается из полуплоскости 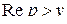 в комплексную плоскость.
в комплексную плоскость.
Замечание 2. Далее всегда будем задавать оригиналы их значениями на полуоси 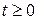 , не оговаривая всякий раз требование
, не оговаривая всякий раз требование 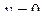 при
при 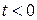 .
.

| 
|
Рис. 2.5. Рис. 2.6.
Задание для самостоятельной работы.
Проверить, что данные функции – оригиналы, и вычислить их 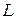 -изобра-жения (2.1):
-изобра-жения (2.1):
а) 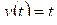 ; б)
; б) 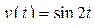 ; в)
; в) 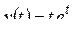 ; г)
; г) 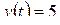 .
.
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
В приложениях операционного исчисления систематически используются следующие правила 10–70. Далее в 20–70 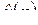 – L-изображение оригинала
– L-изображение оригинала 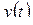 .
.
10 . Теорема линейности:
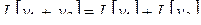 ;
; 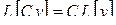
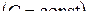 .
.
20. Теорема подобия:
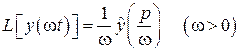 .
.
30. Теорема смещения:
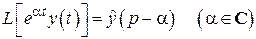 .
.
40. Теорема запаздывания:
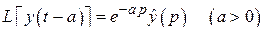 .
.
50. Изображение производных:
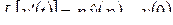 ,
,
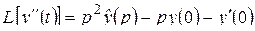 ,
,
. . .
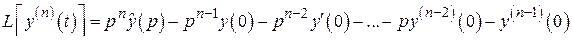 .
.
60. Изображение интеграла:
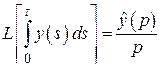 .
.
70.
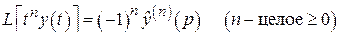 .
.
Свойство 10 непосредственно следует из определения (2.1). Предлагаем читателю доказать свойства 20–50. Отметим, что при доказательстве теоремы запаздывания существенно используется требование 20 в определении оригинала.
Замечание. В приложениях операционного исчисления к теории автоматического управления, радиотехнике, электротехнике оригинал 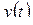 (выходной сигнал линейной стационарной цепи), как правило, удовлетворяет требованию
(выходной сигнал линейной стационарной цепи), как правило, удовлетворяет требованию 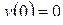 . В этом случае первая формула 50 принимает вид
. В этом случае первая формула 50 принимает вид
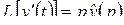 .
.
Это означает: основная операция математического анализа – дифференцирование – в переводе на язык L-изображений 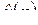 есть операция умножения на независимую переменную p. Аналогично формула 60 означает: другая основная операция математического анализа – интегрирование – в переводе на язык
есть операция умножения на независимую переменную p. Аналогично формула 60 означает: другая основная операция математического анализа – интегрирование – в переводе на язык
L-изображений есть операция деления на независимую переменную p. Эти два факта позволяют в ряде случаев заменить задачи, требующие применение методов математического анализа, равносильными более простыми задачами алгебры. В этом состоит основной замысел операционного исчисления.
Рассмотрим несколько примеров на применение формул 10 – 70.
Примеры. Найти L-изображения следующих функций.
1) 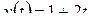 .
.
Решение. По формулам 10, 70 с учетом (2.2) имеем
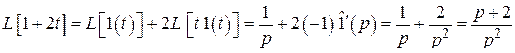 .
.
2) 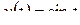 .
.
Решение. По формуле Эйлера (1.3) и формулам 10, (2.3) получим
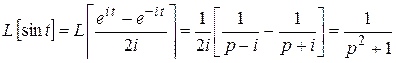 .
.
3) 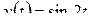 .
.
Решение. Обозначим 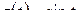 , тогда
, тогда 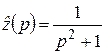 (пример 2). По формуле 20 найдем
(пример 2). По формуле 20 найдем
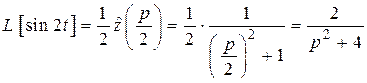 .
.
4) 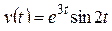 .
.
Решение. Обозначим 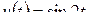 , тогда
, тогда 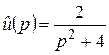 (пример 3). По формуле 30
(пример 3). По формуле 30
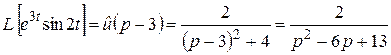 .
.
5) 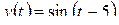 .
.
Решение. Имеем:
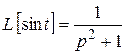 ;
; 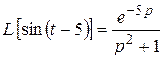 .
.
6) 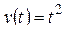 .
.
Решение. Аналогично примеру 1:
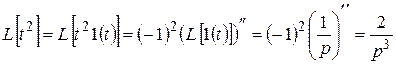 .
.
7) 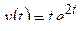 .
.
Решение. По формулам 70 и (2.2):
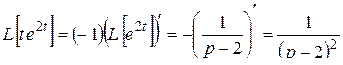 .
.
8) 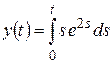 .
.
Решение. По формуле 60
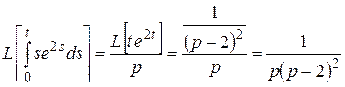
(учтен результат примера 7).
Задание для самостоятельной работы.
Пользуясь свойствами преобразования Лапласа найти L-изображения следующих функций:
а) 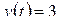 ; б)
; б) 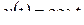 ; в)
; в) 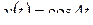 ; г)
; г) 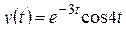 ;
;
д) 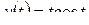 ; е)
; е) 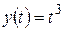 ; ж)
; ж) 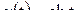 ; з)
; з) 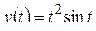 ;
;
и) 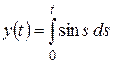 ; к)
; к) 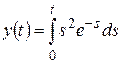 .
.
§ 2.3. ТАБЛИЦА НЕКОТОРЫХ L -ИЗОБРАЖЕНИЙ
Далее при вычислении L-изображений будут использоваться приводимые ниже формулы 1 – 14; первые две доказаны выше, остальные доказываются с помощью приемов, примененных при решении примеров в § 2.2.
| 
|
| 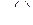
| 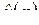
| ||
| 1. | 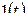
| 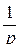
| 8. | 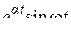
| 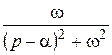
| |
| 2. | 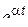
| 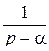
| 9. | 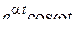
| 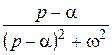
| |
| 3. | 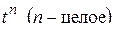
| 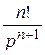
| 10. | 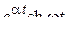
| 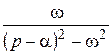
| |
| 4. | 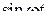
| 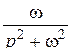
| 11. | 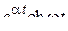
| 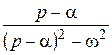
| |
| 5. | 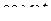
| 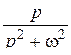
| 12. | 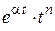
| 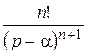
| |
| 6. | 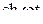
| 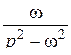
|
| 13. | 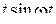
| 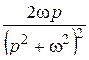
|
| 7. | 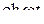
| 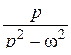
| 14. | 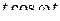
| 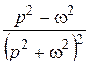
|
Подробные таблицы L-изображений содержатся в книге [7].
Примеры. Пользуясь свойствами преобразования Лапласа и таблицей
L-изображений, найти L-изображения следующих функций.
1) 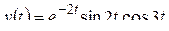 .
.
Решение. Представим произведение 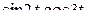 в виде разности синусов:
в виде разности синусов: 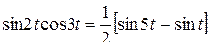 . Пользуясь теоремой линейности и затем формулой 8 из таблицы, получим:
. Пользуясь теоремой линейности и затем формулой 8 из таблицы, получим:
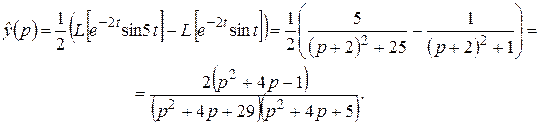
2) 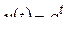
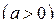 .
.
Решение. Имеем: 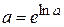 , поэтому
, поэтому 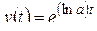 . По формуле 2 из таблицы найдем:
. По формуле 2 из таблицы найдем:
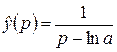 .
.
3) 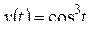 .
.
Решение. Представляя 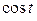 формулой Эйлера, получим:
формулой Эйлера, получим:
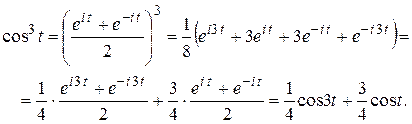
По теореме линейности и формуле 5 из таблицы найдем:
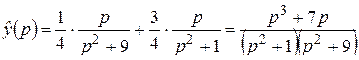 .
.
Задание для самостоятельной работы.
Найти L-изображения следующих функций:
а) 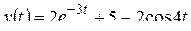 ; б)
; б) 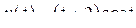 ; в)
; в) 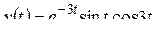 ;
;
г) 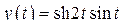 ; д)
; д) 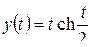 ; е)
; е) 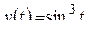 .
.
§ 2.4. ВОССТАНОВЛЕНИЕ ОРИГИНАЛА ПО ЕГО L -ИЗОБРАЖЕНИЮ
Одно из замечательных свойств преобразования Лапласа, широко используемое в приложениях операционного исчисления, состоит в том, что по
L -изображению 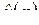 может быть восстановлен оригинал
может быть восстановлен оригинал 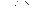 . Имеется общая формула, решающая эту задачу, называемая обратным преобразованием Лапласа (см. книгу [7]) . Эта формула неудобна для практического применения, поэтому мы ее здесь не приводим. Для многих приложений достаточно приводимое ниже частное правило, основанное на теории вычетов для аналитических функций комплексного переменного (§ 1.14).
. Имеется общая формула, решающая эту задачу, называемая обратным преобразованием Лапласа (см. книгу [7]) . Эта формула неудобна для практического применения, поэтому мы ее здесь не приводим. Для многих приложений достаточно приводимое ниже частное правило, основанное на теории вычетов для аналитических функций комплексного переменного (§ 1.14).
Напомним, что рациональная дробь (отношение двух многочленов)
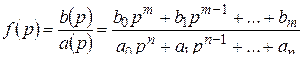
называется правильной, если степень числителя 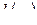 меньше степени знаменателя
меньше степени знаменателя 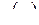 :
: 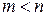 . В силу основной теоремы алгебры комплексных чисел имеет место разложение
. В силу основной теоремы алгебры комплексных чисел имеет место разложение
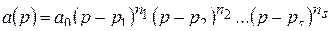 , (2.4)
, (2.4)
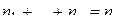 . Очевидно, числа
. Очевидно, числа  являются полюсами функции
являются полюсами функции 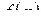 порядков соответственно
порядков соответственно  .
.
Теорема 2.1. Пусть L -изображение 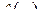 оригинала
оригинала 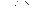 – правильная рациональная дробь со знаменателем (2.4). Тогда оригинал
– правильная рациональная дробь со знаменателем (2.4). Тогда оригинал 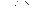 равен сумме вычетов функции
равен сумме вычетов функции 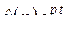 относительно полюсов
относительно полюсов 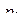 :
:
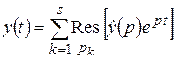 .
.
Эта формула называется формулой обращения. С учетом формулы (1.65) для вычета аналитической функции относительно полюса формула обращения принимает вид
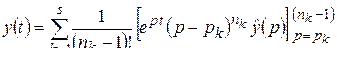 . (2.5)
. (2.5)
Следует помнить, что здесь производная порядка 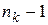 вычисляется (после сокращения в квадратных скобках на
вычисляется (после сокращения в квадратных скобках на 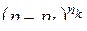 ) по комплексному переменному p при фиксированном t. В частном случае, когда
) по комплексному переменному p при фиксированном t. В частном случае, когда 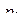 – полюс первого порядка,
– полюс первого порядка, 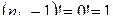 ; под производной порядка 0 понимается сама функция.
; под производной порядка 0 понимается сама функция.
Примеры. Найти оригиналы по данным L-изображениям.
1) 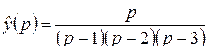 .
.
Решение. Здесь 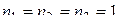 . По формуле обращения (2.5)
. По формуле обращения (2.5)
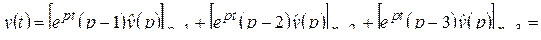
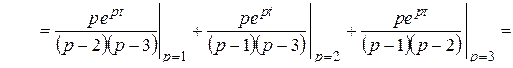
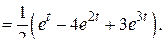
2) 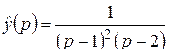 .
.
Решение. По формуле (2.5)
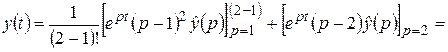
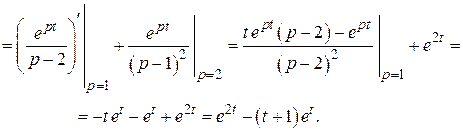
3) 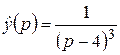 .
.
Решение. По формуле (2.5)
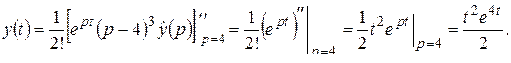
Замечание. Для вычисления оригиналов может быть использовано правило разложения правильной рациональной дроби в сумму простейших дробей. В рассмотренном выше примере 1 разложение имеет вид
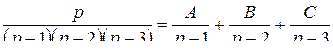 .
.
Вычисления методом неопределенных коэффициентов дают: 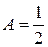 ,
,  ,
, 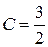 . Применяя к слагаемым формулу 2 из таблицы изображений и затем теорему линейности (справа налево), получим результат
. Применяя к слагаемым формулу 2 из таблицы изображений и затем теорему линейности (справа налево), получим результат
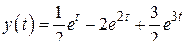 ,
,
совпадающий с полученным выше по формуле обращения. В примере 2 разложение имеет (после вычислений) вид
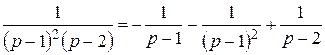 .
.
Применение теоремы линейности и формул 2, 12 из таблицы изображений дает формулу для 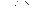 , полученную выше по формуле обращения (проверьте это).
, полученную выше по формуле обращения (проверьте это).
Задание для самостоятельной работы.
Восстановить оригиналы по данным L-изображениям:
а) 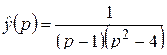 ; б)
; б) 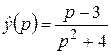 ; в)
; в) 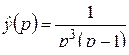 ;
;
г) 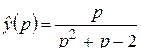 ; д)
; д) 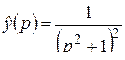 ; е)
; е) 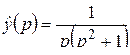 .
.
Дата: 2018-12-28, просмотров: 603.