Определение 1.1. Пусть имеется некоторое множество М комплексных чисел. Если указано правило, по которому каждому числу 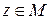 отвечает определенное комплексное число
отвечает определенное комплексное число 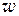 , то говорят, что на множестве М задана функция комплексного переменного z, и пишут так:
, то говорят, что на множестве М задана функция комплексного переменного z, и пишут так:
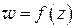 .
.
Множество М называется областью определения 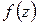 , совокупность N всех значений
, совокупность N всех значений 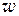 называется областью значений
называется областью значений 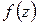 .
.
Чтобы пояснить геометрический смысл функции комплексного переменного, рассмотрим два экземпляра комплексной плоскости: «z-плоскость» и
« 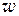 -плоскость» (рис. 1.3).
-плоскость» (рис. 1.3).
Множествам чисел М, N отвечают множества точек соответственно на
z-плоскости и 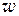 -плоскости. Таким образом, функция комплексного переменного задает отображение множества М точек на плоскости на некоторое другое множество N точек на плоскости[1].
-плоскости. Таким образом, функция комплексного переменного задает отображение множества М точек на плоскости на некоторое другое множество N точек на плоскости[1].

|
Рис. 1.3.
Примерами функций комплексного переменного являются:
линейная функция
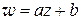 ;
;
дробно-линейная функция
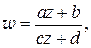
где 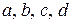 – заданные комплексные числа,
– заданные комплексные числа, 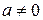 ;
;
степенная функция
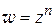 (п – целое число),
(п – целое число),
функции 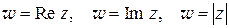 . (1.6)
. (1.6)
Другие примеры функций комплексного переменного будут рассмотрены в § 1.10.
В ближайших параграфах мы распространим на функции комплексного переменного фундаментальные понятия математического анализа: предел, непрерывность, производная, интеграл, затем перейдем к изучению специального класса функций комплексного переменного – так называемых аналитических функций. Совокупность свойств аналитических функций (изучение которых и составляет главное содержание теории функций комплексного переменного) представляет собой мощный аппарат исследования в физике и технике.
Замечание 1. Пусть 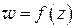 – функция комплексного переменного. Обозначим
– функция комплексного переменного. Обозначим 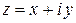 ,
, 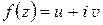 . Тогда, очевидно, u, v – функции от х, у:
. Тогда, очевидно, u, v – функции от х, у:
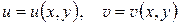 .
.
Таким образом, задание функции комплексного переменного равносильно заданию двух «вещественнозначных» функций двух действительных переменных. Например, пусть 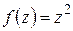 ; тогда получаем:
; тогда получаем:
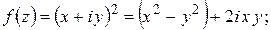
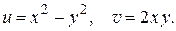
Обратно, зная эти две функции, можем восстановить 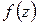 :
:
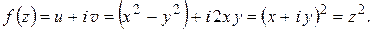
Замечание 2. Если указано правило, по которому каждому числу 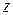 из некоторого множества комплексных чисел M отвечает определенный набор комплексных чисел
из некоторого множества комплексных чисел M отвечает определенный набор комплексных чисел 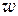 , то говорят, что на множестве М задана многозначная функция. Примером многозначной функции является функция
, то говорят, что на множестве М задана многозначная функция. Примером многозначной функции является функция
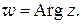
Другой важный пример многозначной функции комплексного переменного будет рассмотрен в § 1.10.
Задание для самостоятельной работы.
1) Найти действительную и мнимую части функций:
а) 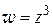 ; б)
; б) 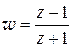 ; в)
; в) 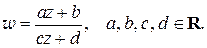
2) На какую линию 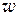 -плоскости отобразится линия
-плоскости отобразится линия 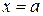
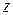 -плоскости с помощью функции
-плоскости с помощью функции 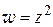 ?
?
Дата: 2018-12-28, просмотров: 456.