Определение 1.2. Комплексное число А будем называть пределом функции комплексного переменного 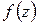 при
при  (и писать
(и писать 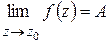 ), если для любого
), если для любого 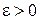 найдется такое
найдется такое 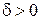 , что для всех
, что для всех 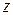 из области определения
из области определения 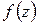 , удовлетворяющих неравенству
, удовлетворяющих неравенству 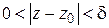 (т. е. лежащих в
(т. е. лежащих в 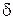 -окрестности точки
-окрестности точки 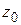 с «выколотым» центром), выполняется неравенство
с «выколотым» центром), выполняется неравенство  .
.
Определение 1.3. Функцию комплексного переменного 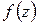 будем называть непрерывной в точке
будем называть непрерывной в точке 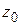 , если 1) точка
, если 1) точка 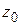 входит в область определения
входит в область определения 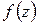 ; 2) существует
; 2) существует 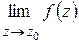 ; 3)
; 3) 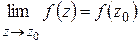 .
.
Определение 1.4. Если функция 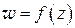 определена в некоторой окрестности точки
определена в некоторой окрестности точки 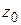 и существует предел
и существует предел
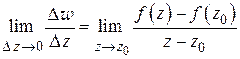
то этот предел называется производной функции 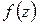 в точке
в точке 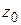 и обозначается
и обозначается 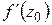 или
или 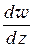 . В этом случае функция
. В этом случае функция 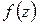 называется дифференцируемой в точке
называется дифференцируемой в точке 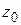 .
.
Так как определения 1.2–1.4 формально совпадают с определениями тех же понятий для функций действительного переменного, то доказанные для последних теоремы о пределе, непрерывности и дифференцируемости суммы, разности, произведения и частного двух функций, о непрерывности и дифференцируемости сложной функции, о непрерывности дифференцируемой функции распространяются без изменений на функции комплексного переменного. Отметим также следующие утверждения:
а) Число 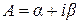 является пределом функции
является пределом функции 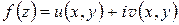 при
при 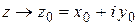 тогда и только тогда, если
тогда и только тогда, если 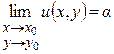 ,
, 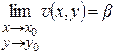 .
.
б) Функция 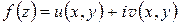 непрерывна в точке
непрерывна в точке 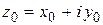 тогда и только тогда, если функции
тогда и только тогда, если функции  непрерывны в точке
непрерывны в точке  .
.
в) Если функция 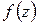 непрерывна на замкнутом ограниченном множестве (т. е. в каждой точке этого множества), то она ограничена на этом множестве, т. е. значения
непрерывна на замкнутом ограниченном множестве (т. е. в каждой точке этого множества), то она ограничена на этом множестве, т. е. значения 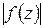 в точках этого множества не превосходят некоторой величины.
в точках этого множества не превосходят некоторой величины.
Предлагаем читателю проверить справедливость а), б) самостоятельно[2].
Производные высших порядков определяются формулой
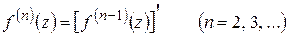 .
.
Важное замечание. В определении производной функции комплексного переменного содержится гораздо более сильное требование, чем в определении того же понятия для функции действительного переменного 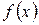 (хотя внешне эти определения совпадают).
(хотя внешне эти определения совпадают).
В самом деле, в определении 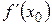 содержится требование существования одинакового предела
содержится требование существования одинакового предела 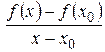 при стремлении х к
при стремлении х к  слева
слева  и справа
и справа 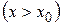 . Определение
. Определение 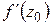 требует существования одинакового предела
требует существования одинакового предела 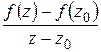 при приближении
при приближении 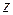 к
к 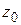 по всем возможным на плоскости направлениям. Этим объясняется то, что дифференцируемые функции комплексного переменного обладают рядом замечательных свойств, не имеющих места для дифференцируемых функций действительного переменного. В частности, в § 1.8 будет показано, что из существования
по всем возможным на плоскости направлениям. Этим объясняется то, что дифференцируемые функции комплексного переменного обладают рядом замечательных свойств, не имеющих места для дифференцируемых функций действительного переменного. В частности, в § 1.8 будет показано, что из существования  в точке
в точке 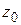 (и некоторой ее окрестности) вытекает существование производных всех порядков
(и некоторой ее окрестности) вытекает существование производных всех порядков 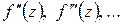 и разложимость
и разложимость 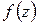 в степенной ряд в точке
в степенной ряд в точке 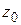 .
.
Пусть функция 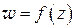 имеет производную в точке
имеет производную в точке 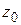 . Вводя обозначение
. Вводя обозначение 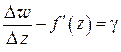 , получим:
, получим:
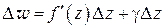 , (1.7)
, (1.7)
где 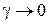 при
при 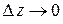 . Подставляя в (1.7)
. Подставляя в (1.7)
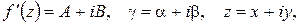
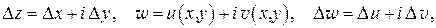 (1.8)
(1.8)
где обозначено
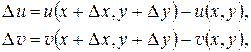
получим равенство
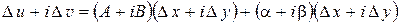 , (1.9)
, (1.9)
откуда следует:
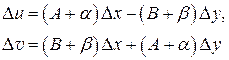 (1.10)
(1.10)
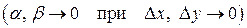 .
.
Напомним, что функция двух переменных 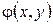 , полное приращение которой
, полное приращение которой 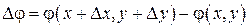 представлено в виде
представлено в виде
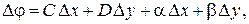
где 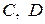 – некоторые постоянные,
– некоторые постоянные,  при
при  , называется дифференцируемой в точке
, называется дифференцируемой в точке 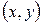 ; при этом
; при этом 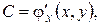
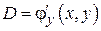 . Следовательно, равенства (1.10) показывают, что функции
. Следовательно, равенства (1.10) показывают, что функции 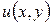 ,
, 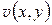 дифференцируемы в точке
дифференцируемы в точке 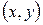 ; при этом
; при этом
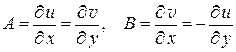 . (1.11)
. (1.11)
Таким образом, нами доказано следующее: если функция комплексного переменного 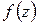 дифференцируема в точке
дифференцируема в точке 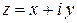 , то ее действительная и мнимая части
, то ее действительная и мнимая части 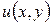 ,
, 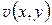 также дифференцируемы в точке
также дифференцируемы в точке 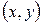 и удовлетворяют в ней условиям
и удовлетворяют в ней условиям
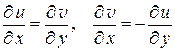 . (1.12)
. (1.12)
Обратно, пусть функции 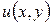 ,
, 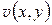 дифференцируемы в точке
дифференцируемы в точке 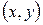 и удовлетворяют в ней условиям (1.12). Тогда, очевидно, выполняются равенства (1.10), где А, В определяются формулами (1.11). Возвращаясь от (1.10) к (1.9) и применяя снова обозначения (1.8), получим:
и удовлетворяют в ней условиям (1.12). Тогда, очевидно, выполняются равенства (1.10), где А, В определяются формулами (1.11). Возвращаясь от (1.10) к (1.9) и применяя снова обозначения (1.8), получим:

где 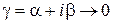 при
при 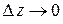 . Деля почленно на
. Деля почленно на 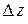 и переходя к пределу при
и переходя к пределу при 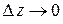 , получим, что
, получим, что
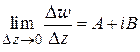 ,
,
т. е. функция 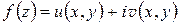 имеет в точке
имеет в точке 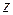 производную, равную
производную, равную 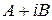 .
.
Равенства (1.12) называются условиями Коши – Римана. Нами доказана следующая теорема.
Теорема 1.1. Для того чтобы функция комплексного переменного  была дифференцируема в данной точке, необходимо и достаточно, чтобы функции
была дифференцируема в данной точке, необходимо и достаточно, чтобы функции 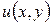 ,
, 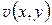 были дифференцируемы в этой точке и удовлетворяли в ней условиям Коши – Римана (1.12). Для производной
были дифференцируемы в этой точке и удовлетворяли в ней условиям Коши – Римана (1.12). Для производной 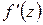 имеют место равенства:
имеют место равенства:
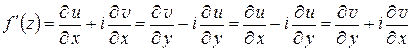 . (1.13)
. (1.13)
Пример 1. Проверить условия Коши – Римана для функции 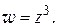
Решение. Имеем:
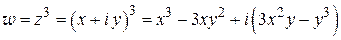 ;
;
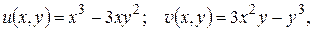
откуда
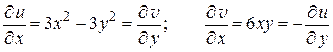 .
.
Условия (1.12) выполнены во всех точках плоскости; следовательно, функция 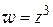 дифференцируема во всей плоскости.
дифференцируема во всей плоскости.
Пример 2. Исследовать на дифференцируемость функцию 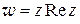 .
.
Решение. Имеем:
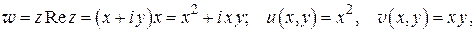
откуда

Условия (1.12) выполнены только в одной точке (0,0); следовательно, функция  дифференцируема только в точке
дифференцируема только в точке 
Задание для самостоятельной работы.
1) Проверить условия Коши – Римана для функции 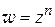 (п – целое число); используя формулу (1.13), доказать, что
(п – целое число); используя формулу (1.13), доказать, что

2) Показать, что функции (1.6) не дифференцируемы ни в одной точке плоскости.
3) Найти точки разрыва функции 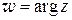 (см. § 1.1).
(см. § 1.1).
§ 1.5. АНАЛИТИЧЕСКИЕ ФУНКЦИИ.
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
Определение 1.5. Если функция 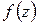 дифференцируема не только в данной точке
дифференцируема не только в данной точке 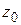 , но и в некоторой окрестности этой точки, то она называется аналитической в точке
, но и в некоторой окрестности этой точки, то она называется аналитической в точке 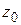 .
.
Определение 1.6. Функция 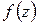 , аналитическая во всех точках области D, называется аналитической в области D.
, аналитическая во всех точках области D, называется аналитической в области D.
В силу теоремы 1.1 для аналитичности функции 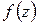 в точке необходимо и достаточно, чтобы условия Коши – Римана (1.12) выполнялись в самой этой точке и в некоторой ее окрестности; для аналитичности в области необходимо и достаточно, чтобы условия (1.12) выполнялись во всех точках этой области.
в точке необходимо и достаточно, чтобы условия Коши – Римана (1.12) выполнялись в самой этой точке и в некоторой ее окрестности; для аналитичности в области необходимо и достаточно, чтобы условия (1.12) выполнялись во всех точках этой области.
Так, функция из примера 1 предыдущего параграфа является аналитичес-кой во всей плоскости. Функция из примера 2 не является аналитической ни в одной точке (из дифференцируемости в отдельной точке не вытекает аналитичность в ней).
Сумма, разность, произведение и частное (при условии неравенства нулю знаменателя) двух аналитических функций, а также сложная функция, составленная из двух аналитических функций, являются аналитическими функциями.
Пусть функция 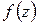 аналитична в области D. Записывая условия Коши –Римана
аналитична в области D. Записывая условия Коши –Римана
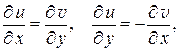
дифференцируя первое из этих тождеств[3] по х, второе по у и складывая, получим:
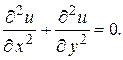 (1.14)
(1.14)
Аналогично, дифференцируя первое тождество по у, второе по х и вычитая, получим:

Дифференциальное уравнение (1.14) называется уравнением Лапласа, а решения этого уравнения называются гармоническими функциями; две гармонические функции 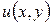 ,
, 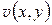 , связанные тождествами (1.12), называются сопряженными. Таким образом доказано: если функция комплексного переменного
, связанные тождествами (1.12), называются сопряженными. Таким образом доказано: если функция комплексного переменного 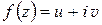 является аналитической в области D, то ее действительная и мнимая части являются сопряженными гармоническими функциями в области D.
является аналитической в области D, то ее действительная и мнимая части являются сопряженными гармоническими функциями в области D.
Обратно, если 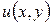 ,
, 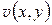 –– сопряженные гармонические функции в области D, то функция
–– сопряженные гармонические функции в области D, то функция 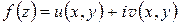 является, очевидно, аналитичес-кой в области D.
является, очевидно, аналитичес-кой в области D.
Замечание. Если дана одна гармоническая функция  , то для отыскания сопряженной к ней нужно, очевидно, решить систему уравнений:
, то для отыскания сопряженной к ней нужно, очевидно, решить систему уравнений:
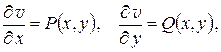 (1.15)
(1.15)
где 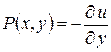 ,
, 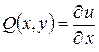 . Так как в этом случае выполнено условие
. Так как в этом случае выполнено условие 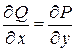 , то эта система разрешима и определяет
, то эта система разрешима и определяет 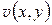 с точностью до постоянного слагаемого. Из сказанного вытекает: зная действительную часть
с точностью до постоянного слагаемого. Из сказанного вытекает: зная действительную часть 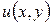 аналитической функции
аналитической функции 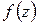 , можно восстановить функцию
, можно восстановить функцию 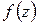 с точ-ностью до постоянного слагаемого.
с точ-ностью до постоянного слагаемого.
Пример. Восстановить 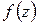 , если
, если 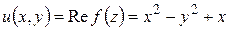 .
.
Решение. Составим систему уравнений (1.15):
 . (*)
. (*)
Из первого уравнения находим
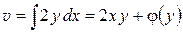 ,
,
где 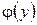 – произвольная (пока) функция от у. Продифференцируем последнее равенство по у:
– произвольная (пока) функция от у. Продифференцируем последнее равенство по у:
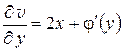 .
.
Сопоставление со вторым уравнением (*) дает 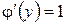 , откуда
, откуда 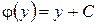 . Таким образом,
. Таким образом, 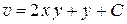 , следовательно,
, следовательно,
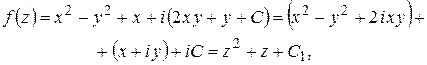
где 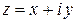 ,
, 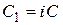 – произвольная постоянная.
– произвольная постоянная.
В заключение этого параграфа приведем электростатический смысл аналитической функции. Пусть в области D на плоскости задано электростатическое поле (поле вектора напряженности)
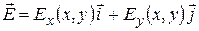 .
.
Потенциалом электростатического поля 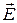 называется функция
называется функция 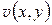 , удовлетворяющая условиям:
, удовлетворяющая условиям:
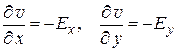 .
.
Предположим, что в области D нет зарядов, тогда во всех точках D
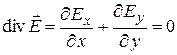 ,
,
откуда
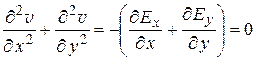 ,
,
т. е. потенциал 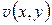 будет гармонической функцией в области D.
будет гармонической функцией в области D.
Функция комплексного переменного
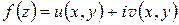 ,
,
где 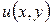 – гармоническая функция, сопряженная к
– гармоническая функция, сопряженная к 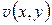 , называется комплексным потенциалом электростатического поля
, называется комплексным потенциалом электростатического поля 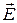 .
.
Очевидно, комплексный потенциал 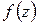 является аналитической функцией в области D. Имеем (см. формулу (1.13)):
является аналитической функцией в области D. Имеем (см. формулу (1.13)):
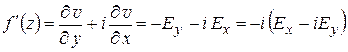 ,
,
откуда

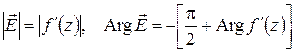 .
.
Функция 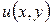 , сопряженная к потенциалу
, сопряженная к потенциалу 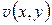 , называется силовой функцией поля
, называется силовой функцией поля 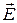 , ее линии уровня (т. е. линии
, ее линии уровня (т. е. линии 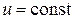 ) называются силовыми линиями; линии уровня функции
) называются силовыми линиями; линии уровня функции 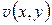 (т. е. линии
(т. е. линии 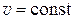 ) называются эквипотенциальными линиями поля
) называются эквипотенциальными линиями поля 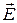 .
.
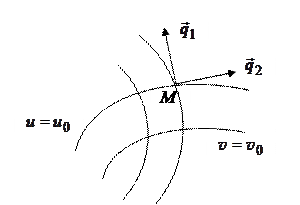
Докажем, что силовые и эквипотенциальные линии образуют ортогональную сеть в области D. В самом деле, в любой точке М области D (рис. 1.4)
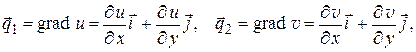
откуда
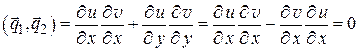
(мы пользовались условиями Коши – Римана (1.12)), т. е. 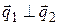 . Так как вектор
. Так как вектор 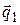 ортогонален касательной к силовой линии в точке М, а вектор
ортогонален касательной к силовой линии в точке М, а вектор 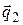 – к эквипотенциальной линии в точке М, то эти линии ортогональны в точке М.
– к эквипотенциальной линии в точке М, то эти линии ортогональны в точке М.
|
Рис. 1.4.
Введение комплексного потенциала позволяет применить хорошо разработанный аппарат теории функций комплексного переменного к исследованию проблем электростатики.
Задание для самостоятельной работы.
1) Найти комплексный потенциал электростатического поля 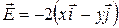 , силовые, эквипотенциальные линии этого поля.
, силовые, эквипотенциальные линии этого поля.
2) Найти длину и направление вектора напряженности электро-статического поля, силовые и эквипотенциальные линии поля по заданному комплексному потенциалу:
а) 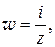 б)
б) 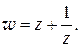
Дата: 2018-12-28, просмотров: 441.