К РЕШЕНИЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Рассмотрим задачу Коши для линейного дифференциального уравнения с постоянными коэффициентами:
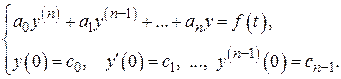 (2.6)
(2.6)
Здесь 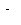 – заданные числа. Будем предполагать, что правая часть
– заданные числа. Будем предполагать, что правая часть  удовлетворяет требованиям 10–30 в определении оригинала. Из теории линейных дифференциальных уравнений следует: в этом случае решение
удовлетворяет требованиям 10–30 в определении оригинала. Из теории линейных дифференциальных уравнений следует: в этом случае решение  и его производные всех порядков также удовлетворяют 10–30.
и его производные всех порядков также удовлетворяют 10–30.
Применяя к обеим частям уравнения (2.6) операцию L, после вычислений с учетом теоремы линейности, формул для L-изображения производных (свойство 50 преобразования Лапласа) и начальных условий (2.6) получим соотношение вида
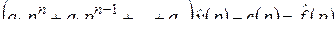 , (2.7)
, (2.7)
где 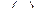 – многочлен с коэффициентами, строящимися по числам
– многочлен с коэффициентами, строящимися по числам 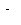 , откуда следует:
, откуда следует:
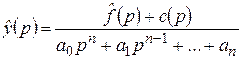 .
.
Применение правила восстановления оригинала по его L-изображению дает искомое решение  задачи Коши (2.6).
задачи Коши (2.6).
Обратим внимание, что в изложенной процедуре наглядно просматривается основной замысел операционного исчисления: дифференциальное уравнение (2.6) для оригинала  заменено эквивалентным существенно более прос-тым алгебраическим уравнением (2.7) для
заменено эквивалентным существенно более прос-тым алгебраическим уравнением (2.7) для  .
.
Примеры. Решить операционным методом следующие задачи Коши.
1) 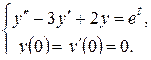
Решение. По теореме линейности имеем:
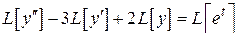 .
.
Формулы 50 § 2.2 для L-изображений производных с учетом начальных условий дают:
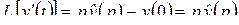 ,
,
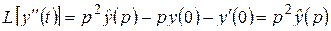 .
.
Подставляя, с учетом равенства 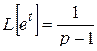 , получим:
, получим:
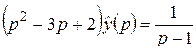 ,
,
откуда
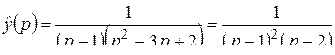 .
.
По формуле обращения (2.5) найдем (см. пример 2 в § 2.4):
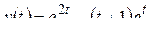
2) 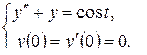
Решение. С учетом формулы 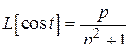 аналогично предыдущему получим
аналогично предыдущему получим
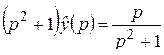 ,
,
откуда
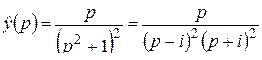 .
.
По формуле обращения
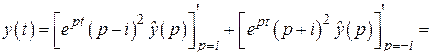
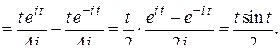
Рекомендуем читателю провести эти вычисления подробно.
§ 2.6. ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
К РЕШЕНИЮ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Рассмотрим задачу Коши для системы линейных дифференциальных уравнений с постоянными коэффициентами
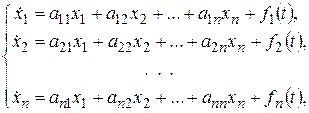

Здесь 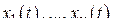 – неизвестные функции,
– неизвестные функции,  – их производные по времени
– их производные по времени 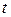 . Обозначим
. Обозначим
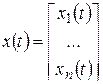 ,
, 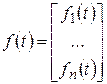 ,
, 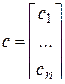 ,
, 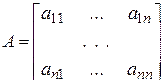 ,
,
тогда задача Коши примет вид
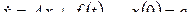 (2.8)
(2.8)
(производная столбца – столбец производных). Будем, как и в § 2.5, предполагать, что правая часть 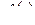 удовлетворяет (поэлементно) требованиям 10–30 в определении оригинала, тогда, в силу теории линейных систем, решение
удовлетворяет (поэлементно) требованиям 10–30 в определении оригинала, тогда, в силу теории линейных систем, решение 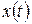 задачи Коши и его производная
задачи Коши и его производная 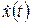 удовлетворяют 10–30.
удовлетворяют 10–30.
Применяя к обеим частям уравнения (2.8) операцию L и вынося постоянный матричный множитель за знак L-изображения, получим:
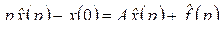
(L-изображение столбца – столбец L-изображений) или, что то же,
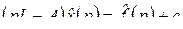 .
.
Здесь I – единичная матрица порядка n, учтено 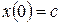 . Умножим обе части равенства слева на матрицу, обратную к
. Умножим обе части равенства слева на матрицу, обратную к 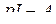 :
:
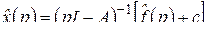 . (2.9)
. (2.9)
Вычисляя по этой формуле по правилам линейной алгебры столбец 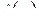 и затем применяя поэлементно правило восстановления оригинала по его L-изображению, получим искомое решение
и затем применяя поэлементно правило восстановления оригинала по его L-изображению, получим искомое решение 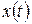 задачи Коши (2.8).
задачи Коши (2.8).
Пример. Решить операционным методом задачу Коши
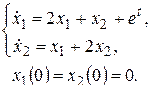
Решение. Вводя обозначения 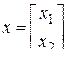 ,
, 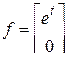 ,
, 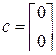 ,
, 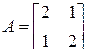 , приведем задачу Коши к виду (2.8). По формуле (2.9)
, приведем задачу Коши к виду (2.8). По формуле (2.9)
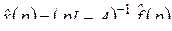 .
.
Здесь
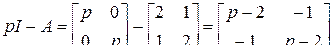 ,
, 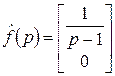 .
.
По формуле для обращения матрицы второго порядка
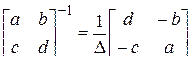 ,
, 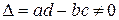
(проверьте ее) получим
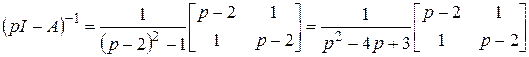 .
.
Таким образом, с учетом 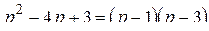 ,
,
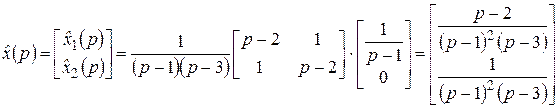 .
.
Вычисления по формуле обращения дают
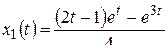 ,
, 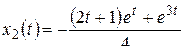 .
.
Задание для самостоятельной работы.
Решить операционным методом задачу Коши:
а) 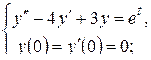 б)
б) 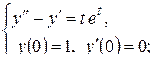 в)
в) 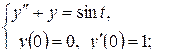
г) 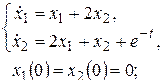 д)
д) 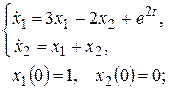 е)
е) 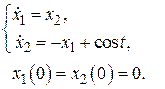
§ 2.7. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
ЛИНЕЙНОЙ СТАЦИОНАРНОЙ ЦЕПИ
В теории автоматического управления широко применяется описание функционирования автоматических устройств на языке «вход – выход»
(рис. 2.7).

| 
|
Рис. 2.7. Рис. 2.8.
Здесь 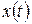 – входной сигнал (входное воздействие),
– входной сигнал (входное воздействие),
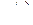 – выходной сигнал (реакция на входное воздействие),
– выходной сигнал (реакция на входное воздействие),
A – правило работы системы:
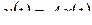 .
.
Определение 2.3. Автоматическое устройство называется линейной цепью, если выполняется принцип суперпозиции:
 ,
,
т.е. если реакция устройства на суперпозицию (результат наложения) нескольких входных воздействий равна сумме реакций на отдельные воздействия.
Определение 2.4. Автоматическое устройство называется стационарной цепью, если форма выходного сигнала полностью определяется формой входного сигнала:
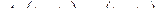 при всех
при всех  .
.
В ряде случаев входной и выходной сигналы линейной стационарной цепи связаны соотношением вида
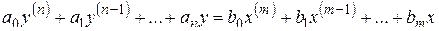 , (2.10)
, (2.10)
где 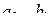 – постоянные; в этой ситуации свойства линейности и стационар-ности следуют из правил теории линейных дифференциальных уравнений. Применяя при нулевых начальных условиях
– постоянные; в этой ситуации свойства линейности и стационар-ности следуют из правил теории линейных дифференциальных уравнений. Применяя при нулевых начальных условиях
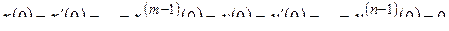
к обеим частям равенства (2.10) операцию L, получим
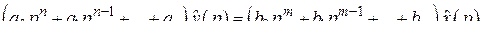 ,
,
откуда
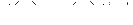 , (2.11)
, (2.11)
где
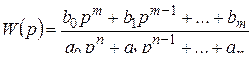 . (2.12)
. (2.12)
Определение 2.5. Рациональная дробь (2.12) называется передаточной функцией линейной стационарной цепи (2.10).
Формула (2.11) задает правило работы цепи на языке L-изображений: на этом языке реакция цепи на входное воздействие сводится к умножению на «передаточный коэффициент» 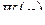 . В теории автоматического управления, радиотехнике, электротехнике широко применяется задание линейных стационарных цепей с помощью передаточной функции (рис. 2.8).
. В теории автоматического управления, радиотехнике, электротехнике широко применяется задание линейных стационарных цепей с помощью передаточной функции (рис. 2.8).
|
Рис. 2.9.
Пример. Входным сигналом радиоприемника является падение напряжения 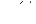 на зажимах антенны, выходным сигналом (с точностью до трансформации электрической энергии в звуковую) – контурный ток
на зажимах антенны, выходным сигналом (с точностью до трансформации электрической энергии в звуковую) – контурный ток 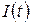 , возбуждаемый в колебательном контуре (рис. 2.9). По второму закону Кирхгофа (закону напряжений) сумма падений напряжения на двуполюсниках
, возбуждаемый в колебательном контуре (рис. 2.9). По второму закону Кирхгофа (закону напряжений) сумма падений напряжения на двуполюсниках 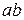 ,
, 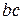 и
и 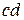 равна падению напряжения на двуполюснике
равна падению напряжения на двуполюснике  :
:
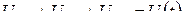 . (2.13)
. (2.13)
По правилам электротехники
 ,
,  ,
, 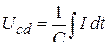 ,
,
где  – положительные постоянные. Подставляя эти выражения в (2.13)
– положительные постоянные. Подставляя эти выражения в (2.13)
и дифференцируя обе части равенства по t (чтобы избавиться от интеграла), получим соотношение вида (2.10):
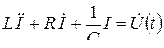 .
.
Применяя к обеим частям при нулевых начальных условиях операцию L,
получим
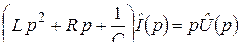 ,
,
откуда 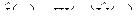 , где
, где
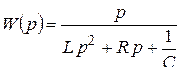 . (2.14)
. (2.14)
Таким образом, радиоприемник – линейная стационарная цепь с передаточной функцией (2.14).
Замечание 1. Фундаментальное свойство линейной стационарной цепи, которое может быть принято за определение, состоит в том, что она переводит одночастотный сигнал (гармонику) в сигнал той же частоты:
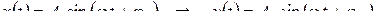 .
.
Отношение
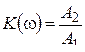
называется коэффициентом усиления на частоте 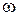 или частотной характеристикой линейной стационарной цепи. Справедлива формула
или частотной характеристикой линейной стационарной цепи. Справедлива формула
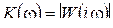 (2.15)
(2.15)
(частотная характеристика равна модулю передаточной функции при 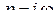 ).
).
В частности, вычисления по формулам (2.14), (2.15) (проведите их) дают частотную характеристику радиоприемника:
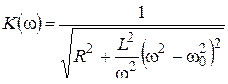 ,
,
где 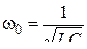 – собственная частота радиоприемника. Эта формула объясняет принцип работы радиоприемника: чтобы услышать сигнал частоты
– собственная частота радиоприемника. Эта формула объясняет принцип работы радиоприемника: чтобы услышать сигнал частоты 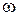 , нужно настроить собственную частоту на входную:
, нужно настроить собственную частоту на входную: 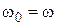 , тогда
, тогда 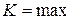 и входной сигнал малой амплитуды становится слышимым.
и входной сигнал малой амплитуды становится слышимым.
Замечание 2. Приведем пример линейной стационарной цепи с векторным выходным сигналом (под вектором понимается столбец, см. рис. 2.10).

|
Рис. 2.10.
Линейная стационарная система автоматического управления (см. книгу [9]) моделируется векторным дифференциальным уравнением вида
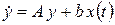 . (2.16)
. (2.16)
Здесь 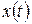 – управляющий сигнал, b – вектор размера n, называемый вектором управляемости, А – матрица управляемого объекта, вектор
– управляющий сигнал, b – вектор размера n, называемый вектором управляемости, А – матрица управляемого объекта, вектор 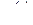 задает состояние управляемого объекта в момент t.
задает состояние управляемого объекта в момент t.
Применяя при нулевых начальных условиях к обеим частям равенства (2.16) операцию L, получим:
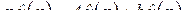 .
.
Как и в § 2.6, L-изображение вектора вычисляется поэлементно. Найдем отсюда 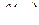 :
:
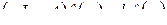 , откуда
, откуда
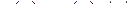 , где
, где 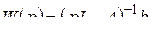 . (2.17)
. (2.17)
Очевидно, при каждом p 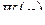 – вектор-столбец. Таким образом, система управления (2.16) – линейная стационарная цепь с передаточной вектор-функцией (2.17).
– вектор-столбец. Таким образом, система управления (2.16) – линейная стационарная цепь с передаточной вектор-функцией (2.17).
Дата: 2018-12-28, просмотров: 436.