Аппарат степенных рядов позволяет естественным образом продолжить функции действительного переменного  ,
, 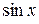 ,
, 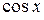 и некоторые другие в комплексную область.
и некоторые другие в комплексную область.
Так как разложения в ряды
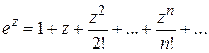 , (1.36)
, (1.36)
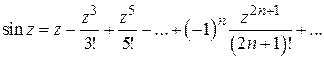 , (1.37)
, (1.37)
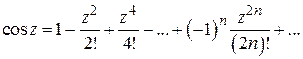 (1.38)
(1.38)
справедливы при любых действительных 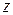 , то в силу теоремы Абеля ряды в правых частях сходятся при любых комплексных
, то в силу теоремы Абеля ряды в правых частях сходятся при любых комплексных 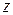 . Формулы (1.36)–(1.38) примем за определения
. Формулы (1.36)–(1.38) примем за определения 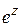 ,
, 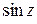 ,
,  при комплексном
при комплексном 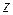 .
.
При таких определениях  ,
, 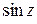 ,
, 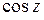 являются аналитическими функциями во всей плоскости (см. следствие из теорем 1.4, 1.5), совпадающими на действительной оси с соответствующими функциями действительного переменного. Дифференцируя почленно ряды (1.36) – (1.38), получим:
являются аналитическими функциями во всей плоскости (см. следствие из теорем 1.4, 1.5), совпадающими на действительной оси с соответствующими функциями действительного переменного. Дифференцируя почленно ряды (1.36) – (1.38), получим:
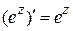 ,
, 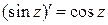 ,
, 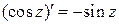 .
.
Теорема 1.6. При любых комплексных 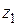 ,
, 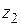 справедливы формулы сложения
справедливы формулы сложения
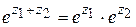 , (1.39)
, (1.39)
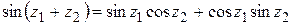 . (1.40)
. (1.40)
Доказательство. Зафиксируем какое-либо действительное значение 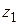 . Тогда левая и правая части (1.39) являются функциями от
. Тогда левая и правая части (1.39) являются функциями от 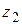 , совпадающими на действительной оси (так как для действительных значений
, совпадающими на действительной оси (так как для действительных значений 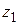 ,
,  формула (1.39) верна). Так как эти функции аналитичны во всей плоскости, то по свойству единственности аналитических функций (см. § 1.8, замечание 1) они совпадают при всех комплексных значениях
формула (1.39) верна). Так как эти функции аналитичны во всей плоскости, то по свойству единственности аналитических функций (см. § 1.8, замечание 1) они совпадают при всех комплексных значениях 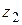 . Зафиксируем теперь любое комплексное значение
. Зафиксируем теперь любое комплексное значение  . Тогда левая и правая части (1.39) являются аналитическими функциями от
. Тогда левая и правая части (1.39) являются аналитическими функциями от 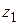 и в силу доказанного совпадают на действительной оси. Следовательно, они совпадают и при всех комплексных значениях
и в силу доказанного совпадают на действительной оси. Следовательно, они совпадают и при всех комплексных значениях 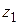 , т. е. формула (1.39) верна при любых комплексных
, т. е. формула (1.39) верна при любых комплексных  ,
, 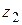 . Аналогично может быть доказана формула (1.40).
. Аналогично может быть доказана формула (1.40).
Теорема 1.7. При любом комплексном 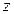 справедлива формула Эйлера
справедлива формула Эйлера
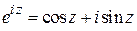 . (1.41)
. (1.41)
Доказательство. Из (1.36) – (1.38) вытекает:
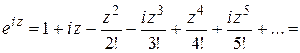

Из (1.36), (1.41) в качестве элементарных следствий вытекают такие формулы (предлагаем читателю проверить их самостоятельно):
а) При любом комплексном 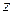


б) При любом комплексном 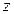

(т. е.  является периодической функцией с периодом
является периодической функцией с периодом 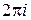 ).
).
в) Если 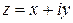 , то
, то
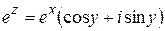 .
.
г) Комплексное число 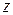 с модулем
с модулем 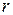 и аргументом
и аргументом 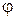 можно представить в виде
можно представить в виде
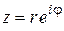 . (1.42)
. (1.42)
Выражение (1.42) называется показательной формой комплексного числа 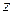 .
.
Функции 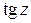 ,
,  определяются равенствами
определяются равенствами
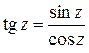 ,
, 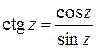 .
.
Гиперболические функции определяются равенствами:
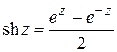 ,
, 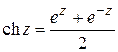 ,
, 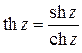 ,
,  .
.
Нетрудно установить тождества:
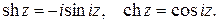
Комплексное число 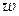 будем называть натуральным логарифмом комплексного числа
будем называть натуральным логарифмом комплексного числа 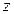 , если
, если
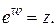 (1.43)
(1.43)
Так как вместе с 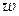 условию (1.43) удовлетворяет число
условию (1.43) удовлетворяет число  , то логарифм
, то логарифм 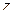 имеет много значений. Чтобы найти все значения логарифма
имеет много значений. Чтобы найти все значения логарифма 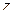 , подставим в (1.43)
, подставим в (1.43)
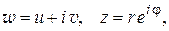
где  – главное значение аргумента
– главное значение аргумента 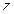 (см. § 1.1). Тогда получим
(см. § 1.1). Тогда получим  ; откуда
; откуда 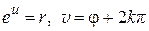 , т. е.
, т. е.
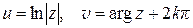
( 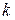 – целое число). Следовательно, обозначая общее значение логарифма
– целое число). Следовательно, обозначая общее значение логарифма 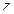 через
через 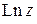 , получим:
, получим:
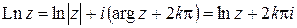
( 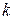 – произвольное целое число), где обозначено:
– произвольное целое число), где обозначено:
 . (1.44)
. (1.44)
Выражение (1.44) будем называть главным значением натурального логарифма 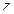 . Очевидно, при
. Очевидно, при 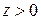
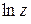 совпадает с обычным логарифмом
совпадает с обычным логарифмом 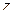 .
.
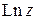 является примером многозначной функции (см. замечание к § 1.2).
является примером многозначной функции (см. замечание к § 1.2).
Задание для самостоятельной работы.
1) Доказать (1.40), не опираясь на свойство единственности аналитических функций.
2) Проверить справедливость утверждений а) – г).
3) Доказать периодичность тригонометрических и гиперболических фун-кций комплексного переменного, найти «наименьшие» периоды для 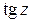 и
и 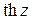 .
.
4) Вычислить 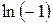 ,
,  ,
, 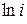 ,
, 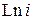 .
.
5) Найти область существования и точки разрыва функции 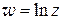 .
.
6) Доказать формулы 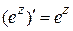 ,
, 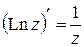 , используя формулу (1.13).
, используя формулу (1.13).
РЯД ТЕЙЛОРА
Рассмотрим функцию 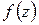 , аналитическую внутри круга
, аналитическую внутри круга 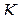 с центром в точке
с центром в точке 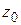 . Покажем, что
. Покажем, что 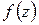 разлагается в этом круге в степенной ряд вида (1.33).
разлагается в этом круге в степенной ряд вида (1.33).
Пусть  – любая точка внутри круга
– любая точка внутри круга 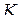 . Проведем внутри
. Проведем внутри 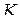 окружность
окружность 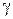 с центром в точке
с центром в точке  так, чтобы точка
так, чтобы точка 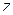 оказалась внутри этой окружности. Тогда значение функции в точке
оказалась внутри этой окружности. Тогда значение функции в точке 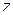 можно представить интегральной формулой Коши:
можно представить интегральной формулой Коши:
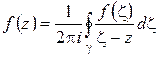 . (1.45)
. (1.45)
Рассмотрим отдельно множитель 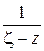 :
:
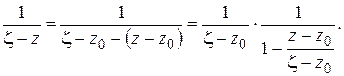 (1.46)
(1.46)
Если точка 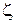 лежит на окружности
лежит на окружности 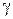 , то
, то 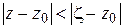 (рис. 1.12), поэтому
(рис. 1.12), поэтому
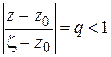
и второй множитель правой части (1.46) является суммой геометрической прогрессии:
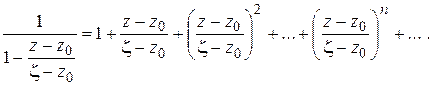 (1.47)
(1.47)

|
Рис. 1.12.
Из (1.46), (1.47) вытекает, что подынтегральную функцию в правой части (1.45) можно представить в виде суммы ряда:
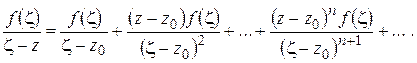 (1.48)
(1.48)
Учитывая, что значения 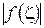 в точках окружности
в точках окружности 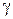 не превосходят некоторой величины М (по свойству непрерывных функций), получим для всех
не превосходят некоторой величины М (по свойству непрерывных функций), получим для всех 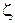 на
на 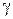 :
:
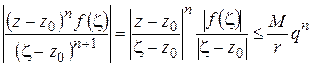
( 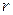 – радиус
– радиус 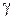 ). Так как числовой ряд
). Так как числовой ряд  сходится (геометрическая прогрессия,
сходится (геометрическая прогрессия,  ), то ряд (1.48) правильно сходится на
), то ряд (1.48) правильно сходится на 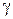 . Подставляя (1.48) в правую часть (1.45) и почленно интегрируя, получим:
. Подставляя (1.48) в правую часть (1.45) и почленно интегрируя, получим:
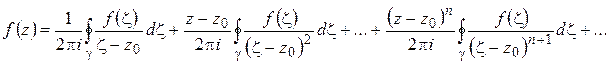
или
 (1.49)
(1.49)
где
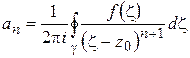 . (1.50)
. (1.50)
Мы представили значение функции в произвольной точке круга 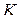 рядом (1.49) с коэффициентами (1.50). Отметим, что коэффициенты (1.50) одни и те же для всех точек
рядом (1.49) с коэффициентами (1.50). Отметим, что коэффициенты (1.50) одни и те же для всех точек  из круга
из круга 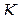 , так как в силу следствия из теоремы Коши величина интеграла (1.50) одна и та же для всех окружностей
, так как в силу следствия из теоремы Коши величина интеграла (1.50) одна и та же для всех окружностей 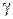 с центром в точке
с центром в точке 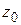 , лежащих внутри круга
, лежащих внутри круга 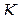 .
.
Ряд (1.49) с коэффициентами (1.50) называется рядом Тейлора. Таким образом, доказана
Теорема 1.8. Любая функция 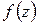 , аналитическая внутри круга с центром
, аналитическая внутри круга с центром 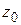 , разлагается внутри этого круга в ряд Тейлора (1.49).
, разлагается внутри этого круга в ряд Тейлора (1.49).
Сопоставляя формулу (1.50) с доказанной формулой (1.28) для производных аналитической функции, получим знакомые выражения для коэффициентов ряда Тейлора:
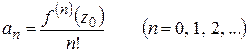 .
.
Замечание 1. Если функция 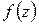 аналитична в точке
аналитична в точке 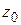 , т. е. дифференцируема в некоторой ее окрестности, то по теореме 1.8 она разлагается в этой окрестности в степенной ряд (1.49). Обратно, если
, т. е. дифференцируема в некоторой ее окрестности, то по теореме 1.8 она разлагается в этой окрестности в степенной ряд (1.49). Обратно, если 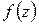 разлагается в степенной ряд в некоторой окрестности точки
разлагается в степенной ряд в некоторой окрестности точки 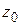 , то по следствию из теоремы 1.5 она аналитична в этой окрестности, а значит, и в точке
, то по следствию из теоремы 1.5 она аналитична в этой окрестности, а значит, и в точке 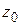 . Таким образом, утверждения «
. Таким образом, утверждения « 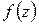 аналитична в точке
аналитична в точке 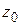 », «
», « 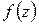 разлагается в степенной ряд в окрестности точки
разлагается в степенной ряд в окрестности точки 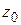 » равносильны. Этим отчасти объясняется термин «аналитическая функция»: она может быть аналитически задана в виде степенного ряда. В дальнейшем читатель должен воспринимать термин «аналитическая функция» как «разлагающаяся в степенной ряд».
» равносильны. Этим отчасти объясняется термин «аналитическая функция»: она может быть аналитически задана в виде степенного ряда. В дальнейшем читатель должен воспринимать термин «аналитическая функция» как «разлагающаяся в степенной ряд».
Замечание 2. Из теоремы 1.8 следует: радиус сходимости ряда Тейлора (1.49) равен расстоянию от точки 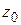 до ближайшей к
до ближайшей к 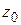 особой точки (т. е. точки, в которой
особой точки (т. е. точки, в которой 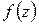 не является аналитической).
не является аналитической).
Замечание 3. Если значения 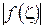 на контуре
на контуре 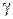 в формуле (1.50) не превосходят числа М, то, пользуясь оценкой (1.18) модуля интеграла, получим:
в формуле (1.50) не превосходят числа М, то, пользуясь оценкой (1.18) модуля интеграла, получим:
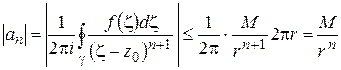
(здесь  – радиус
– радиус 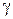 ); таким образом,
); таким образом,
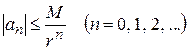 . (1.51)
. (1.51)
Неравенства (1.51) называются неравенствами Коши для коэффициентов ряда Тейлора.
Если 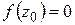 , то точка
, то точка 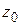 называется нулем функции
называется нулем функции 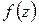 . Предполагая
. Предполагая 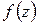 аналитической в точке
аналитической в точке 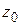 , разложим ее в степенной ряд в окрестности
, разложим ее в степенной ряд в окрестности  ; тогда, очевидно,
; тогда, очевидно,  . Если при этом
. Если при этом 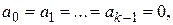
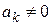 , то число
, то число 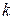 будем называть порядком нуля
будем называть порядком нуля 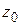 . В этом случае
. В этом случае
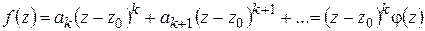 ,
,
где 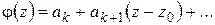 – функция, аналитическая в точке
– функция, аналитическая в точке 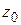 и не равная нулю в этой точке:
и не равная нулю в этой точке: 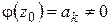 . Обратно, если
. Обратно, если  , где
, где 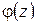 удовлетворяет указанным условиям, то, разложив
удовлетворяет указанным условиям, то, разложив 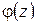 в ряд Тейлора в точке
в ряд Тейлора в точке  , получим:
, получим:
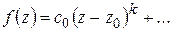 ,
,
где 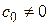 , т. е.
, т. е. 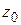 – нуль
– нуль 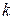 -го порядка
-го порядка 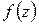 .
.
Например, точки  ,
, 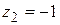 являются нулями первого порядка (или простыми нулями) функции
являются нулями первого порядка (или простыми нулями) функции 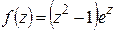 :
: 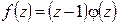 , где
, где 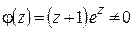 при
при 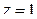 ; аналогично
; аналогично 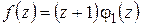 , где
, где 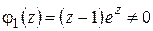 при
при 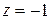 .
.
Задание для самостоятельной работы.
1) Разложить в ряд Тейлора: а) 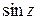 в точке
в точке 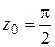 ; б)
; б)  в точке
в точке 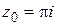 .
.
2) Найти радиус сходимости ряда Тейлора функции 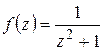 в точке
в точке 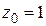 (см. замечание 2).
(см. замечание 2).
3) Найти нули функции и определить их порядки: а) 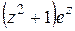 ; б)
; б) 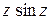 ; в)
; в) 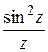 ; г)
; г) 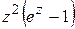 .
.
4) Доказать единственность разложения в ряд Тейлора:
если 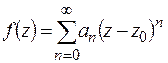 ,
, 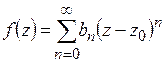 , то
, то 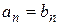
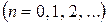 .
.
РЯД ЛОРАНА
Рассмотрим функцию 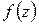 , аналитическую внутри кольца между двумя окружностями с центром
, аналитическую внутри кольца между двумя окружностями с центром 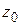 (в частном случае кольцо может быть кругом с «выколотым» центром). Проведем окружности
(в частном случае кольцо может быть кругом с «выколотым» центром). Проведем окружности 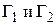 с центром в точке
с центром в точке 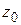 так, чтобы каждая из них находилась внутри данного кольца и чтобы точка
так, чтобы каждая из них находилась внутри данного кольца и чтобы точка  оказалась между ними. Из точки
оказалась между ними. Из точки 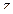 как из центра проведем окружность
как из центра проведем окружность 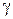 , лежащую между
, лежащую между 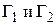 (рис. 1.13).
(рис. 1.13).

|
Рис. 1.13.
В силу следствия из теоремы Коши имеем:
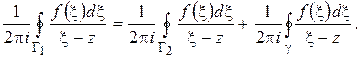
На основании интегральной формулы Коши последний из этих трех интегралов равен  , поэтому получаем:
, поэтому получаем:
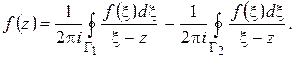 (1.52)
(1.52)
Первое слагаемое правой части на основании вычислений § 1.11 представляется рядом
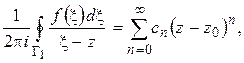
где
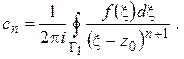 (1.53)
(1.53)
Чтобы разложить в ряд второе слагаемое, заметим, что если  , то
, то  , поэтому
, поэтому
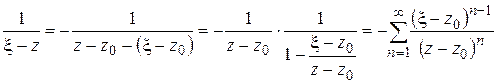 ,
,
откуда
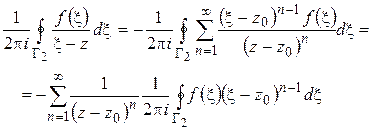
или
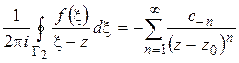 ,
,
где
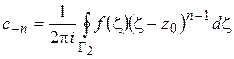 (1.54)
(1.54)
(возможность почленного интегрирования проверяется так же, как в предыдущем параграфе). Заметим, что в формулах (1.53), (1.54) в качестве контура интегрирования можно взять любую окружность  с центром в точке
с центром в точке 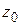 , лежащую внутри кольца (по следствию из теоремы Коши), поэтому формулы (1.53), (1.54) можно объединить в одну следующим образом:
, лежащую внутри кольца (по следствию из теоремы Коши), поэтому формулы (1.53), (1.54) можно объединить в одну следующим образом:
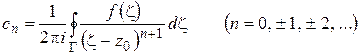 . (1.55)
. (1.55)
Подставляя полученные разложения в (1.52), получим:
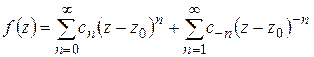
или
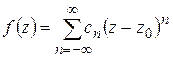 (1.56)
(1.56)
с коэффициентами (1.55).
Ряд (1.56) называется рядом Лорана.
Таким образом, доказана
Теорема 1.9. Любая функция  , аналитическая внутри кольца с центром
, аналитическая внутри кольца с центром  , разлагается внутри этого кольца в ряд Лорана (1.56) с коэффициентами (1.55).
, разлагается внутри этого кольца в ряд Лорана (1.56) с коэффициентами (1.55).
Пример. Разложить функцию  в ряд Лорана в кольце
в ряд Лорана в кольце 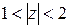 .
.
Решение. Вначале разложим  на простейшие дроби:
на простейшие дроби:
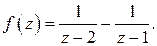
Разложим в ряд каждое слагаемое отдельно, используя примененный выше прием: разложение в бесконечно убывающую геометрическую прогрессию. Так как в данном кольце 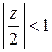 ,
, 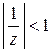 , то
, то
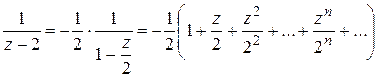 ;
;
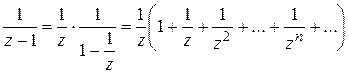 .
.
Вычитая эти разложения, получим:
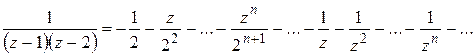
Замечание. Если в формуле (1.55) значения  на контуре
на контуре  не превосходят числа М и радиус
не превосходят числа М и радиус  равен
равен  , то, повторяя вычисления, проведенные в § 1.11 (замечание 3), получим оценки для модулей коэффициентов ряда Лорана:
, то, повторяя вычисления, проведенные в § 1.11 (замечание 3), получим оценки для модулей коэффициентов ряда Лорана:
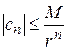 (
( 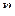 = 0, ±1, ±2, …).
= 0, ±1, ±2, …).
Задание для самостоятельной работы.
1) Разложить в ряд Лорана: а) 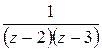 в кольце
в кольце 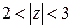 и в кольце
и в кольце 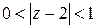 ; б)
; б) 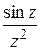 в кольце
в кольце 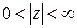 .
.
2) Доказать единственность разложения в ряд Лорана:
если 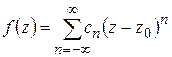 и
и 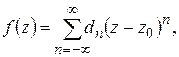
то 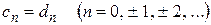 .
.
§ 1.13. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
АНАЛИТИЧЕСКОЙ ФУНКЦИИ
Точки плоскости, в которых функция 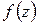 является аналитической, будем называть правильными точками этой функции, а точки, в которых
является аналитической, будем называть правильными точками этой функции, а точки, в которых  не является аналитической (в частности, точки, в которых
не является аналитической (в частности, точки, в которых  не определена), – особыми точками. Особая точка называется изолированной, если в некоторой ее окрестности нет других особых точек.
не определена), – особыми точками. Особая точка называется изолированной, если в некоторой ее окрестности нет других особых точек.
Если 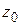 есть изолированная особая точка
есть изолированная особая точка 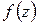 , то в достаточно малом круге с «выколотым» центром
, то в достаточно малом круге с «выколотым» центром  функция
функция  будет аналитической и, следовательно, разлагается в ряд Лорана
будет аналитической и, следовательно, разлагается в ряд Лорана
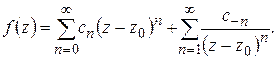 (1.57)
(1.57)
Ряд 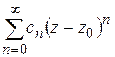 назовем правильной частью, ряд
назовем правильной частью, ряд 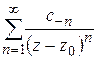 – главной частью разложения (1.57). Возможны три случая:
– главной частью разложения (1.57). Возможны три случая:
1) В разложении (1.57) отсутствует главная часть (т. е. все коэффициенты  ).
).
2) Главная часть содержит конечное число членов.
3) Главная часть содержит бесконечное число членов.
В этих случаях особая точка  называется соответственно 1) устранимой, 2) полюсом, 3) существенно особой точкой.
называется соответственно 1) устранимой, 2) полюсом, 3) существенно особой точкой.
В случае устранимой особой точки из (1.57) следует 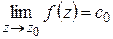 . Если доопределить
. Если доопределить  в точке
в точке 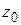 , приняв
, приняв  , то
, то  станет правильной точкой
станет правильной точкой 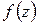 (особенность «устраняется»).
(особенность «устраняется»).
Если 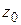 – полюс, то
– полюс, то
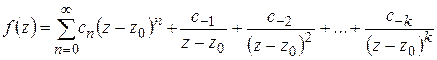 , (1.58)
, (1.58)
где 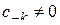 .
.
После приведения к общему знаменателю получим:
 , (1.59)
, (1.59)
где обозначено:
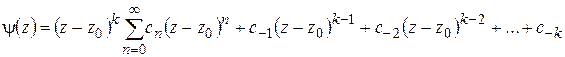 .
.
Последнее равенство показывает, что функция 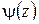 является аналитичес-кой в точке
является аналитичес-кой в точке 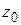 и
и 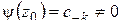 .
.
Таким образом, если точка 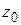 является полюсом функции
является полюсом функции 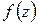 , то в окрестности этой точки
, то в окрестности этой точки 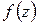 изображается в виде (1.59), где
изображается в виде (1.59), где 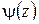 аналитична в точке
аналитична в точке  и
и 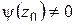 . Обратно, если
. Обратно, если 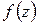 имеет вид (1.59), где
имеет вид (1.59), где 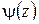 удовлетворяет указанным условиям, то, разлагая
удовлетворяет указанным условиям, то, разлагая 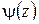 в ряд Тейлора в точке
в ряд Тейлора в точке  и выполняя почленное деление на
и выполняя почленное деление на 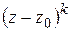 , получим разложение вида (1.58), откуда следует, что
, получим разложение вида (1.58), откуда следует, что 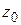 – полюс
– полюс  .
.
Число 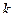 называется порядком полюса. Полюс первого порядка называется простым полюсом.
называется порядком полюса. Полюс первого порядка называется простым полюсом.
Заметим следующее: функция 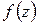 имеет в точке
имеет в точке  полюс
полюс 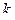 -го порядка тогда и только тогда, если функция
-го порядка тогда и только тогда, если функция 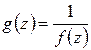 имеет в точке
имеет в точке 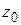 нуль такого же порядка (см. конец § 1.11). В самом деле, из (1.59) (с выполнением указанных условий для
нуль такого же порядка (см. конец § 1.11). В самом деле, из (1.59) (с выполнением указанных условий для 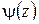 ) следует:
) следует:
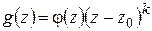 ,
,
где 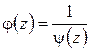 аналитична и не равна нулю в точке
аналитична и не равна нулю в точке 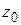 , т. е.
, т. е.  является нулем
является нулем 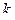 -го порядка для
-го порядка для 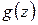 ; обратный переход выполняется так же.
; обратный переход выполняется так же.
Из формулы (1.59) вытекает:
если 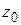 – полюс
– полюс  , то
, то
 .
.
Таким образом, поведение аналитической функции в окрестности полюса может быть описано следующим образом: при стремлении к  по любому направлению
по любому направлению  .
.
Чтобы выяснить поведение функции в окрестности существенно особой точки, рассмотрим следующий пример. Пусть 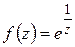 . Тогда из формулы (1.36) вытекает:
. Тогда из формулы (1.36) вытекает:
при 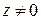
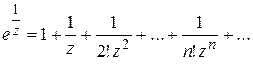 (1.60)
(1.60)
Так как это разложение содержит бесконечно много членов с отрицательными степенями  , то точка является существенно особой точкой для
, то точка является существенно особой точкой для 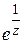 . Обратим внимание на следующее: если
. Обратим внимание на следующее: если  стремится к нулю слева (
стремится к нулю слева ( 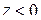 ), то
), то 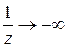 и
и 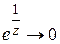 ; если
; если 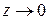 справа (
справа ( 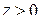 ), то
), то 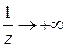 и
и 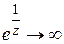 . Эти элементарные соображения показывают, что поведение функции в окрестности существенно особой точки более сложно, чем в окрестности устранимой особой точки и полюса. Можно доказать, что справедлива следующая теорема Сохоцкого: если
. Эти элементарные соображения показывают, что поведение функции в окрестности существенно особой точки более сложно, чем в окрестности устранимой особой точки и полюса. Можно доказать, что справедлива следующая теорема Сохоцкого: если 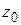 – существенно особая точка аналитической функции
– существенно особая точка аналитической функции  , то для любого комплексного числа
, то для любого комплексного числа 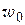 найдется последовательность точек
найдется последовательность точек 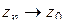 такая, что
такая, что  .
.
Задание для самостоятельной работы.
1) Найти особые точки функции и определить их характер (для полюсов указать их порядки):
а)  ; б)
; б) 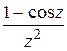 ; в)
; в) 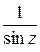 ; г)
; г) 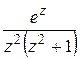 ; д)
; д) 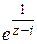 .
.
2) Будет ли точка  изолированной особой точкой для функции
изолированной особой точкой для функции 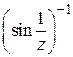 ?
?
ВЫЧЕТЫ
Пусть 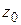 – изолированная особая точка аналитической функции
– изолированная особая точка аналитической функции  ; тогда в окрестности этой точки
; тогда в окрестности этой точки  изобразится рядом Лорана (1.57).
изобразится рядом Лорана (1.57).
Определение 1.11. Коэффициент при 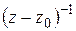 в разложении Лорана (1.57), т. е. число
в разложении Лорана (1.57), т. е. число 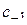 называется вычетом функции
называется вычетом функции  относительно особой точки
относительно особой точки 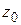 и обозначается
и обозначается 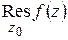 :
:
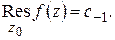
Например, из (1.60) вытекает:  .
.
Из формулы (1.55) для коэффициентов ряда Лорана следует:
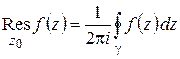 , (1.61)
, (1.61)
где  – окружность с центром
– окружность с центром  достаточно малого радиуса.
достаточно малого радиуса.
Роль вычетов выясняет следующая
Теорема 1.10 (основная теорема о вычетах). Если функция 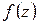 аналитична внутри замкнутого контура
аналитична внутри замкнутого контура  и на самом контуре, за исключением конечного числа точек
и на самом контуре, за исключением конечного числа точек 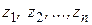 внутри
внутри  , то интеграл
, то интеграл 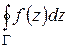 равен произведению числа
равен произведению числа 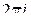 на сумму вычетов относительно особых точек, лежащих внутри
на сумму вычетов относительно особых точек, лежащих внутри  :
:
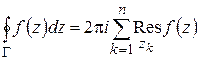 . (1.62)
. (1.62)
Доказательство. Проведем окружности 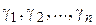 с центрами соответственно
с центрами соответственно 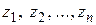 столь малых радиусов, чтобы все окружности лежали внутри
столь малых радиусов, чтобы все окружности лежали внутри  , не имели общих точек и внутри каждой окружности находилась только одна особая точка (рис. 1.14). Тогда в силу следствия из теоремы Коши
, не имели общих точек и внутри каждой окружности находилась только одна особая точка (рис. 1.14). Тогда в силу следствия из теоремы Коши
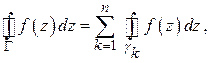
откуда, вследствие (1.61), и вытекает формула (1.62).
 
|
Рис. 1.14.
Доказанная теорема показывает: если мы научимся практически находить вычеты, то это даст нам подход к вычислению интегралов от функций комплексного переменного. Укажем некоторые приемы вычисления вычетов.
1) Пусть 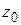 – простой полюс
– простой полюс 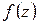 :
:
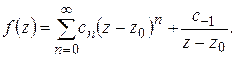
Умножая почленно на 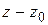 и переходя к пределу при
и переходя к пределу при 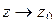 , получим:
, получим:
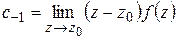 . (1.63)
. (1.63)
Пусть теперь 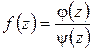 , где
, где 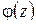 ,
, 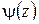 аналитичны в точке
аналитичны в точке 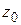 и
и 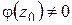 ,
, 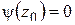 ,
, 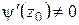 . Последнее условие означает, что
. Последнее условие означает, что  является простым нулем
является простым нулем 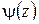 и, следовательно, простым полюсом для
и, следовательно, простым полюсом для 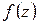 . Формула (1.63) дает:
. Формула (1.63) дает:
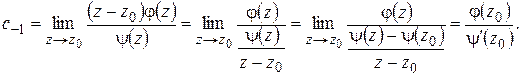
Итак, в этом случае
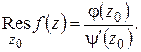 (1.64)
(1.64)
Например, 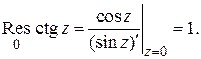
2) Пусть  – полюс второго порядка
– полюс второго порядка  :
:
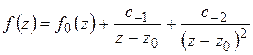 ,
,
где 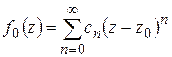 . Умножая почленно на
. Умножая почленно на 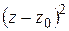 и дифференцируя полученное равенство по
и дифференцируя полученное равенство по  , получим:
, получим:
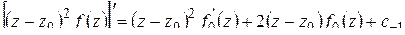 ,
,
откуда
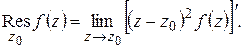
Например,
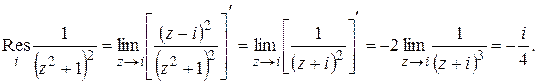 (*)
(*)
Аналогичным вычислением может быть найден вычет относительно полюса
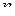 -го порядка:
-го порядка:
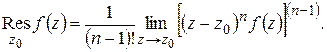 (1.65)
(1.65)
3) В ряде случаев вычет может быть найден путем разложения в ряд Лорана.
Пример 1. Найти 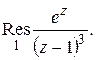
Решение. Имеем:
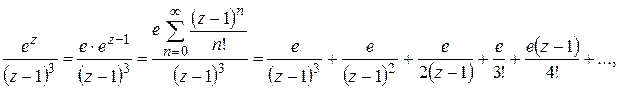
откуда 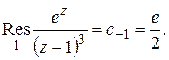
Пример 2. Вычислить 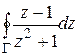 , где Г – окружность
, где Г – окружность 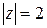 .
.
Решение. Оба полюса 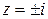 лежат внутри Г, поэтому, применяя формулы (1.62), (1.64), получим:
лежат внутри Г, поэтому, применяя формулы (1.62), (1.64), получим:
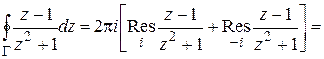
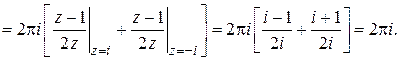
Задание для самостоятельной работы.
1) Найти вычеты следующих функций относительно каждого из полюсов:
а) 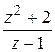 ; б)
; б) 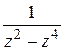 ; в)
; в) 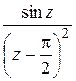 ; г)
; г) 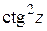 ; д)
; д) 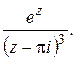
2) Вычислить  , где Г – окружность
, где Г – окружность 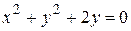 .
.
§ 1.15. ПРИМЕНЕНИЕ ВЫЧЕТОВ
К ВЫЧИСЛЕНИЮ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
С помощью вычетов могут быть вычислены некоторые несобственные интегралы от функций действительного переменного.
Теорема 1.11. Если функция  аналитична на действительной оси и в верхней полуплоскости, за исключением конечного числа точек
аналитична на действительной оси и в верхней полуплоскости, за исключением конечного числа точек 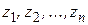
в верхней полуплоскости, и если  при
при 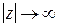 стремится к нулю быстрее, чем
стремится к нулю быстрее, чем  :
:
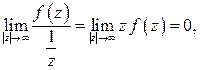 (1.66)
(1.66)
то
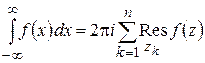 . (1.67)
. (1.67)
Доказательство. При достаточно большом 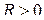 все особые точки
все особые точки 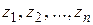 будут лежать внутри полукруга, ограниченного сегментом
будут лежать внутри полукруга, ограниченного сегментом 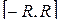 и верхней половиной
и верхней половиной 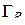 окружности
окружности 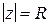 (рис. 1.15). Тогда в силу основной теоремы о вычетах
(рис. 1.15). Тогда в силу основной теоремы о вычетах
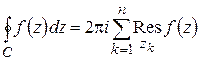 (1.68)
(1.68)
(С – граница полукруга); с другой стороны,
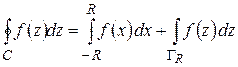 .
.

|
Рис. 1.15.
Заменяя левую часть величиной (1.68) и переходя к пределу при 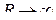 , получим:
, получим:
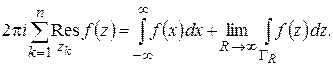
Остается показать, что последний предел равен нулю. Зададимся произвольным 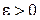 . Тогда по условию (1.66) существует такое
. Тогда по условию (1.66) существует такое 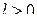 , что при
, что при 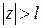 будет
будет  . Но
. Но 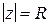 в точках полуокружности
в точках полуокружности 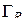 ; следовательно, если взять
; следовательно, если взять 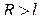 , то при
, то при 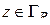 будет:
будет:
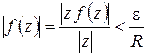 ;
;
тогда в силу (1.18)
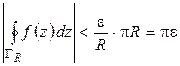 .
.
Таким образом, показано, что, выбирая радиус  полуокружности
полуокружности  достаточно большим, мы можем сделать величину
достаточно большим, мы можем сделать величину 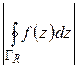 сколь угодно малой, а это и значит, что
сколь угодно малой, а это и значит, что 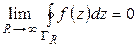 . Теорема доказана.
. Теорема доказана.
Пример 1. Вычислить
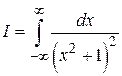 .
.
Решение. Функция 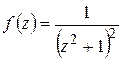 аналитична на действительной оси, имеет в верхней полуплоскости только одну особую точку
аналитична на действительной оси, имеет в верхней полуплоскости только одну особую точку 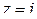 и удовлетворяет условию (1.66).
и удовлетворяет условию (1.66).
Следовательно, применяя формулу (1.67) и используя ранее полученный результат (*), находим:
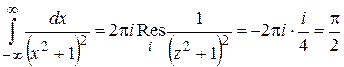 .
.
При вычислении несобственных интегралов иногда бывает полезна следующая лемма (приводим ее без доказательства):
Лемма Жордана. Если функция  имеет вид:
имеет вид:
 , (1.69)
, (1.69)
где 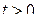 ,
, 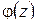 аналитична на действительной оси и в верхней полуплоскости, за исключением конечного числа точек
аналитична на действительной оси и в верхней полуплоскости, за исключением конечного числа точек  , и
, и 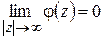 , то имеет место формула (1.67).
, то имеет место формула (1.67).
Пример 2. Вычислить
 .
.
Решение. Обратим внимание, что для этого интеграла условие (1.66) не выполняется. Далее заметим, что
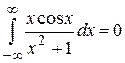
(так как функция 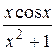 нечетная). Поэтому
нечетная). Поэтому
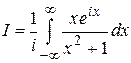 .
.
Подынтегральная функция имеет вид (1.69): 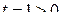 ,
, 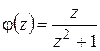 – аналитична на действительной оси, имеет в верхней полуплоскости полюс
– аналитична на действительной оси, имеет в верхней полуплоскости полюс  ,
, 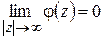 . Поэтому на основании леммы Жордана и формулы (1.64)
. Поэтому на основании леммы Жордана и формулы (1.64)
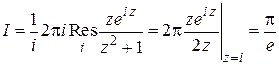 .
.
В заключение этого параграфа рассмотрим пример на вычисление несобственного интеграла с использованием теоремы Коши (теорема 1.2).
Пример 3. Вычислить интеграл Пуассона 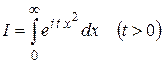 .
.
Решение. Функция 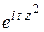 аналитична во всей плоскости, поэтому в силу теоремы Коши интеграл от нее по границе сектора ОАВ (рис. 1.16) равен нулю:
аналитична во всей плоскости, поэтому в силу теоремы Коши интеграл от нее по границе сектора ОАВ (рис. 1.16) равен нулю:
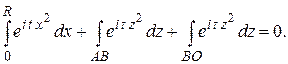
Переходя к пределу при  , получим
, получим 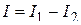 , где
, где


|
Рис. 1.16.
На отрезке 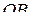
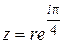
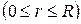 , поэтому
, поэтому
 .
.
(Здесь использовано, что 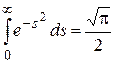 ). На дуге
). На дуге 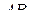
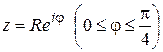 , поэтому
, поэтому
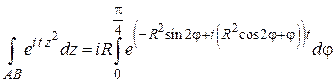 .
.
Откуда, учитывая неравенство  , получим
, получим
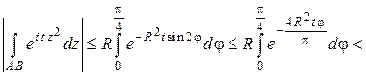
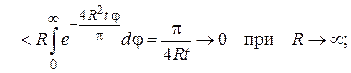
следовательно, 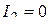 . Таким образом
. Таким образом
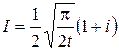 .
.
ПРИНЦИП АРГУМЕНТА
Укажем правило подсчета числа нулей и полюсов аналитической функции внутри заданного контура.
Теорема 1.12. Пусть функция 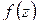 не имеет нулей и особых точек на замкнутом контуре
не имеет нулей и особых точек на замкнутом контуре  и имеет внутри
и имеет внутри  конечное число особых точек, являющихся полюсами. Тогда разность между числом нулей и числом полюсов функции
конечное число особых точек, являющихся полюсами. Тогда разность между числом нулей и числом полюсов функции 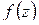 внутри контура
внутри контура  равна числу оборотов, которые описывает вектор, соединяющий начало координат с точкой
равна числу оборотов, которые описывает вектор, соединяющий начало координат с точкой 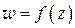 , при однократном обходе точкой
, при однократном обходе точкой  контура
контура  в положительном направлении (при этом каждый нуль и каждый полюс засчитывается столько раз, какова их кратность).
в положительном направлении (при этом каждый нуль и каждый полюс засчитывается столько раз, какова их кратность).
Доказательство. Напомним: если точка 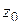 – нуль порядка
– нуль порядка  функции
функции 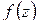 , то в окрестности точки
, то в окрестности точки 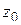
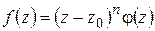 , (1.70)
, (1.70)
где 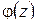 аналитична в точке
аналитична в точке 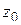 и
и 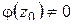 . Из (1.70) вытекает:
. Из (1.70) вытекает:

и
 .
.
Функция 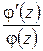 аналитична в точке
аналитична в точке  ; следовательно, функция
; следовательно, функция  имеет простой полюс в точке
имеет простой полюс в точке 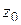 и
и
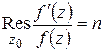 .
.
Аналогично, если 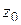 – полюс порядка m функции
– полюс порядка m функции 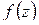 , то в окрестности
, то в окрестности 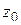
 ,
,
где 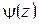 аналитична в точке
аналитична в точке 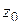 и
и 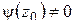 . Повторяя вычисления, получим:
. Повторяя вычисления, получим:
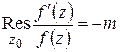 .
.
Так как на  нет нулей и полюсов
нет нулей и полюсов 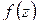 , то функция
, то функция 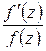 аналитична на
аналитична на  . Обозначая нули и полюса
. Обозначая нули и полюса 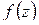 внутри
внутри  соответственно через
соответственно через 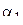 , …,
, …, 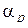 ,
, 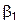 , …,
, …, 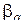 , по основной теореме о вычетах получим:
, по основной теореме о вычетах получим:
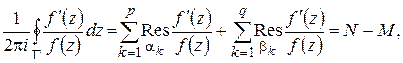 (1.71)
(1.71)
где N – сумма кратностей нулей 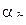 , M – сумма кратностей полюсов
, M – сумма кратностей полюсов  . С другой стороны, учитывая, что
. С другой стороны, учитывая, что 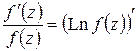 , по формуле Ньютона – Лейбница для аналитических функций (см. § 1.7) имеем:
, по формуле Ньютона – Лейбница для аналитических функций (см. § 1.7) имеем:
 ,
,
где правая часть означает приращение, которое получает 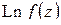 , когда точка
, когда точка  описывает контур
описывает контур  в положительном направлении. Так как
в положительном направлении. Так как
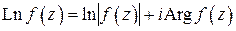 ,
,
то
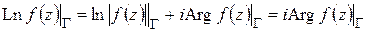
(функция 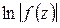 непрерывна на
непрерывна на  и после обхода возвращается к первоначальному значению) и
и после обхода возвращается к первоначальному значению) и
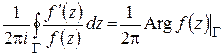 .
.
Правая часть этого равенства выражает число оборотов, которые описывает вектор, соединяющий начало координат с точкой 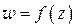 , когда точка
, когда точка  описывает
описывает  в положительном направлении. Сопоставляя с (1.71), получим:
в положительном направлении. Сопоставляя с (1.71), получим:
 ,
,
что и требовалось доказать.
Доказанное правило называется принципом аргумента. Очевидно, в частном случае, если внутри  нет полюсов
нет полюсов 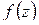 , принцип аргумента дает возможность подсчитать число нулей
, принцип аргумента дает возможность подсчитать число нулей 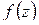 внутри
внутри  .
.
Пример. Доказать, что многочлен степени п
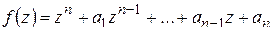
имеет ровно п нулей.
Решение. Имеем
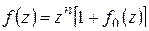 , (1.72)
, (1.72)
где
 .
.
Так как 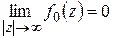 , то существует такое
, то существует такое 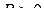 , что при
, что при 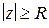 будет
будет 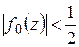 ; следовательно, точка, изображающая
; следовательно, точка, изображающая 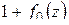 , будет лежать внутри круга радиуса
, будет лежать внутри круга радиуса 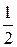 с центром в точке
с центром в точке  (рис. 1.17). Из сказанного вытекает, что: а) все нули
(рис. 1.17). Из сказанного вытекает, что: а) все нули 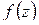 лежат внутри окружности
лежат внутри окружности 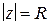 ; б) когда точка
; б) когда точка  описывает окружность
описывает окружность 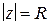 в положительном направлении, точка
в положительном направлении, точка 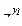 (первый множитель в (1.72)) делает п полных оборотов вокруг нуля, точка
(первый множитель в (1.72)) делает п полных оборотов вокруг нуля, точка 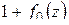 (второй множитель (1.72)) – ни одного; следовательно, точка
(второй множитель (1.72)) – ни одного; следовательно, точка  делает п полных оборотов. В силу принципа аргумента число нулей
делает п полных оборотов. В силу принципа аргумента число нулей 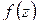 равно n, что и требовалось доказать.
равно n, что и требовалось доказать.

|
Рис. 1.17.
Доказанное утверждение называется основной теоремой алгебры.
ПРИНЦИП МАКСИМУМА
Применим принцип аргумента для обоснования другого фундаменталь-ного правила теории функций – принципа максимума. Сначала докажем следующую лемму.
Лемма 1.2. Если функция 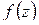 аналитична в точке
аналитична в точке 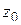 ,
, 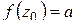 ,
, 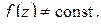 то существует окрестность точки
то существует окрестность точки 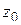 , не содержащая корней уравнения
, не содержащая корней уравнения 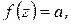 кроме точки
кроме точки 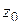 .
.
Доказательство. Так как 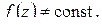 то в разложении Тейлора
то в разложении Тейлора 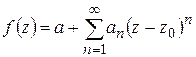 хотя бы одно из чисел
хотя бы одно из чисел 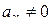 , поэтому имеем:
, поэтому имеем:
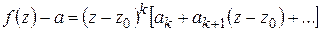 , (1.73)
, (1.73)
где 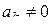 . С другой стороны, если в любой близости точки
. С другой стороны, если в любой близости точки 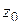 имелись бы корни уравнения
имелись бы корни уравнения 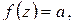 то существовала бы последовательность точек
то существовала бы последовательность точек 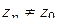 ,
, 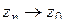 ,
, 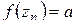 . Подставляя в (1.73)
. Подставляя в (1.73) 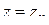 и учитывая, что
и учитывая, что 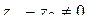 , получили бы
, получили бы
 ;
;
переходя к пределу при  , получили бы
, получили бы 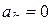 . Полученное противоречие доказывает лемму.
. Полученное противоречие доказывает лемму.
Теорема 1.13 (принцип максимума). Если функция 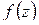 , не равная постоянной, непрерывна в ограниченной замкнутой области
, не равная постоянной, непрерывна в ограниченной замкнутой области 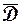 и аналитична во внутренних точках
и аналитична во внутренних точках 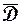 , то ее модуль достигает наибольшего значения на границе области
, то ее модуль достигает наибольшего значения на границе области 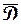 .
.
Доказательство. Так как функция 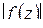 непрерывна в замкнутой ограниченной области
непрерывна в замкнутой ограниченной области 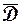 , то она достигает наибольшего значения в некоторой точке
, то она достигает наибольшего значения в некоторой точке 
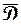 :
:
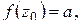
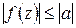 при
при 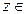
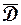 . (1.74)
. (1.74)
Геометрически это означает, что все точки  при
при 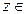
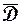 лежат в круге
лежат в круге 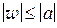 на
на 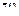 -плоскости (рис. 1.19). Покажем, что
-плоскости (рис. 1.19). Покажем, что 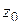 – граничная точка
– граничная точка 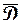 .
.
В самом деле, пусть 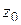 – внутренняя точка
– внутренняя точка 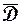 . Тогда
. Тогда 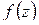 удовлетворяет в точке
удовлетворяет в точке 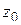 условиям леммы 1.2, и поэтому существует столь малая окружность
условиям леммы 1.2, и поэтому существует столь малая окружность 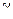 с центром
с центром 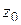 , что на
, что на 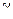 и внутри
и внутри 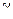 нет нулей функции
нет нулей функции  кроме точки
кроме точки 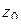 (можно считать, что
(можно считать, что 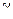 с внутренностью целиком лежит внутри
с внутренностью целиком лежит внутри 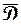 (рис. 1.18)). Обозначив
(рис. 1.18)). Обозначив 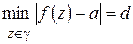 (очевидно,
(очевидно, 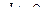 ) и выбрав точку
) и выбрав точку 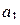 так, что
так, что  ,
, 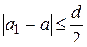 (рис. 1.19), будем иметь:
(рис. 1.19), будем иметь:
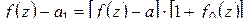 ,
,
где
 ,
, 
при 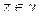 .
.
При обходе точкой  окружности
окружности 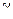 в положительном направлении первый множитель в правой части делает не менее одного оборота вокруг нуля (в силу принципа аргумента), второй – ни одного (рис. 1.17), следовательно, функция
в положительном направлении первый множитель в правой части делает не менее одного оборота вокруг нуля (в силу принципа аргумента), второй – ни одного (рис. 1.17), следовательно, функция 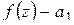 имеет хотя бы один нуль
имеет хотя бы один нуль 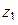 внутри
внутри 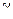 :
: 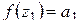 . Получено противоречие с (1.74), теорема доказана.
. Получено противоречие с (1.74), теорема доказана.
Теорема 1.14. Функция 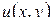 , гармоническая в замкнутой ограниченной области
, гармоническая в замкнутой ограниченной области  и не равная постоянной, достигает наибольшего и наименьшего значения на границе области
и не равная постоянной, достигает наибольшего и наименьшего значения на границе области 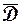 .
.
Доказательство. Обозначим 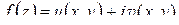 , где
, где  – гармоническая в
– гармоническая в  функция, сопряженная
функция, сопряженная 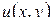 (см. § 1.5). Тогда функция
(см. § 1.5). Тогда функция 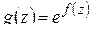 удовлетворяет в области
удовлетворяет в области  условиям теоремы 1.13 и, следовательно, ее модуль
условиям теоремы 1.13 и, следовательно, ее модуль 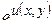 достигает наибольшего значения на границе
достигает наибольшего значения на границе  ; отсюда вытекает, что
; отсюда вытекает, что 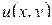 достигает наибольшего значения на границе
достигает наибольшего значения на границе  . Вводя вместо
. Вводя вместо 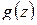 функцию
функцию 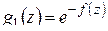 , убедимся, что наименьшее значение
, убедимся, что наименьшее значение 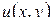 также достигается на границе
также достигается на границе 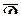 .
.
Теорема 1.14 геометрически означает, что график гармонической функции 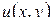 есть поверхность (рельеф) без вершин и впадин.
есть поверхность (рельеф) без вершин и впадин.

| 
|
Рис. 1.18. Рис. 1.19.
Задание для самостоятельной работы.
1) Доказать: если функция 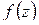 удовлетворяет в области
удовлетворяет в области 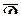 условиям теоремы 1.14 и не имеет нулей в
условиям теоремы 1.14 и не имеет нулей в 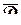 , то ее модуль достигает наименьшего значения на границе
, то ее модуль достигает наименьшего значения на границе 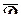 .
.
2) Найти графики (рельефы) гармонических функций:
а) 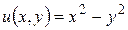 ; б)
; б) 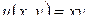 ; в)
; в) 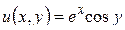 .
.
Дата: 2018-12-28, просмотров: 480.