Рассмотрим в верхней полуплоскости 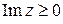 функцию
функцию
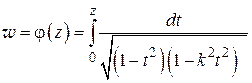 , (1.81)
, (1.81)
где 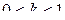 .
.

|
Рис. 1.25.
Имеем:
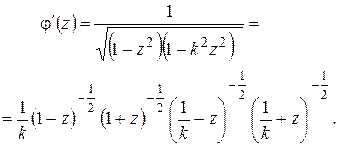 (1.82)
(1.82)
Из (1.82) видно, что производная 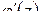 существует (и не равна нулю) всюду, кроме точек
существует (и не равна нулю) всюду, кроме точек 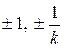 (рис. 1.25). Далее заметим следующее:
(рис. 1.25). Далее заметим следующее:
1) на каждом интервале действительной оси, не содержащем особых точек, каждая из скобок в правой части (1.82) сохраняет знак, и поэтому аргумент производной 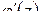 сохраняет постоянное значение;
сохраняет постоянное значение;
2) при переходе через каждую особую точку слева направо (по «малой» дуге в верхней полуплоскости) аргумент одной из скобок уменьшается на  (рис. 1.26), аргументы остальных скобок не меняются, поэтому аргумент производной
(рис. 1.26), аргументы остальных скобок не меняются, поэтому аргумент производной 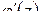 увеличивается на
увеличивается на 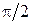 .
.
Из пунктов 1), 2) и из геометрического смысла производной вытекает, что при отображении (1.81) действительная ось переходит в ломаную линию с прямыми углами при вершинах, при этом особые точки 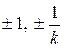 переходят в вершины ломаной. Перемещению точки
переходят в вершины ломаной. Перемещению точки 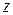 по действительной оси слева направо отвечает перемещение ее образа
по действительной оси слева направо отвечает перемещение ее образа 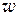 по ломаной против часовой стрелки.
по ломаной против часовой стрелки.

|
Рис. 1.26.
Более подробные рассмотрения показывают, что эта ломаная представляет собой границу прямоугольника 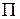 , расположенного, как показано на рис. 1.27; стороны этого прямоугольника могут быть найдены по формулам
, расположенного, как показано на рис. 1.27; стороны этого прямоугольника могут быть найдены по формулам
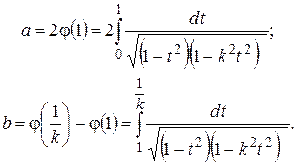 (1.83)
(1.83)

|
Рис. 1.27.
Из сказанного и из сформулированного выше (в замечании) правила вытекает, что функция 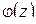 , определяемая формулой (1.81), конформно отображает верхнюю полуплоскость
, определяемая формулой (1.81), конформно отображает верхнюю полуплоскость 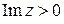 в прямоугольник П со сторонами (1.83). Можно доказать, что это отображение взаимно однозначно.
в прямоугольник П со сторонами (1.83). Можно доказать, что это отображение взаимно однозначно.
Функция (1.81) называется эллиптическим интегралом первого рода. Для вычисления значений этой функции составлены таблицы; в частности, с помощью таблиц могут быть вычислены величины (1.83).
Пусть теперь требуется найти конформное и взаимно однозначное отображение верхней полуплоскости на прямоугольник 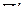 с заданными сторонами
с заданными сторонами 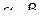 , расположенный так, как показано на рис. 1.28. Вначале, пользуясь таблицами эллиптических интегралов, нужно подобрать значение параметра
, расположенный так, как показано на рис. 1.28. Вначале, пользуясь таблицами эллиптических интегралов, нужно подобрать значение параметра 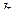 так,
так,

|
Рис. 1.28.
чтобы выполнялось соотношение 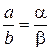 , тогда функция
, тогда функция 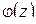 , отвечающая этому значению
, отвечающая этому значению 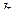 , отображает конформно и взаимно однозначно верхнюю полуплоскость на прямоугольник П, подобный данному. Затем нужно последовательно выполнить преобразования сжатия с коэффициентом
, отображает конформно и взаимно однозначно верхнюю полуплоскость на прямоугольник П, подобный данному. Затем нужно последовательно выполнить преобразования сжатия с коэффициентом 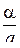 , поворота на угол
, поворота на угол 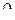 и переноса на величину
и переноса на величину 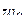 ; окончательная формула для искомого отображения, как легко убедиться, такова:
; окончательная формула для искомого отображения, как легко убедиться, такова:
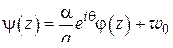 .
.
В заключение отметим, что функция, обратная к функции 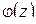 , называется эллиптическим синусом и обозначается
, называется эллиптическим синусом и обозначается 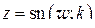 ; очевидно, она отображает прямоугольник П на верхнюю полуплоскость.
; очевидно, она отображает прямоугольник П на верхнюю полуплоскость.
Задание для самостоятельной работы.
1) Отобразить конформно и взаимно однозначно область 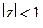 на каждую из указанных областей:
на каждую из указанных областей:
а) 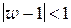 ; б)
; б) 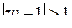 ; в)
; в) 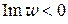 ; г)
; г) 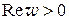 .
.
2) Отобразить конформно и взаимно однозначно на единичный круг каждую из указанных областей:
а) 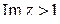 ; б)
; б) 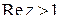 ; в)
; в) 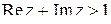 ; г)
; г) 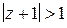 .
.
3) Найти конформное и взаимно однозначное отображение внешности единичного круга на верхнюю полуплоскость, при котором мнимая ось переходит в себя.
4) На какую область плоскости отображает:
а) функция 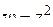 область
область 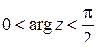 ;
;
б) функция 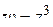 область
область 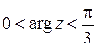 ,
, 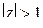 ;
;
в) функция 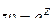 область
область 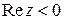 ,
, 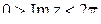 ?
?
5) Отобразить конформно и взаимно однозначно на верхнюю полуплоскость каждую из следующих областей:
а) общую часть кругов 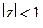 ,
, 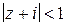 ;
;
6) общую часть кругов 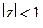 ,
, 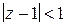 .
.
Дата: 2018-12-28, просмотров: 840.