Чтобы научиться решать эту задачу, нужно прежде всего по­добрать функцию, которая переводит окружности в окружности или прямые (рис. 1.23, 1.24). Оказывается, таким свойством обладает дробно-линейная функция.

Рис. 1.23.

Напомним, что дробно-линейной функцией называется функция вида

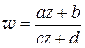,                                                    (1.76)

где a, b, с, d – комплексные постоянные; будем предполагать, что

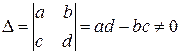
(в противном случае будет ). Очевидно, функция (1.76) определена во всей -плоскости, кроме точки 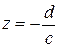, при этом производная 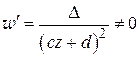. Далее, подставляя в левую часть (1.76) любое комплексное число  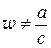и решая (1.76) относи­тельно 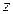, найдем

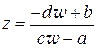                                             (1.77)

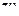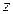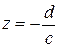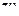 (это и есть то значение, которое переходит в  при отображении (1.76)). Таким образом, дробно-линейная функция (1.76) отобра­жает конформно и взаимно однозначно -плоскость с «выколотой» точкой  на -плоскость с «выколотой» точкой .

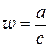Рис. 1.24.

Теорема 1.15. Дробно-линейная функция переводит любую окружность в окружность или прямую; любую прямую – также в окружность или прямую.

Доказательство. Заметим, что уравнение окружности и прямой можно записать единой формулой

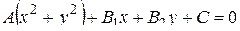
(при 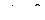 оно определяет окружность, при  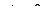– прямую).

Пе­реходя к комплексным обозначениям, перепишем это уравнение в виде

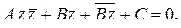                                   (1.78)

где 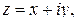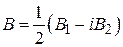. Подставляя вместо  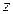выражение (1.77), после преобразований получим:

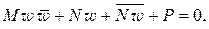                                 (1.79)

где обозначено

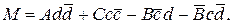
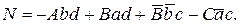
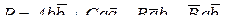
Уравнение (1.79) имеет такую же структуру, как (1.78), и, следовательно, определяет окружность или прямую на -плоскости; теорема доказана.

Доказанное утверждение называется круговым свойством дробно-линейной функции. Если считать прямую линию частным случаем окружности – окружностью бесконечного радиуса, то круговое свойство можно сформулировать так: дробно-линейная функция переводит окружность в окружность.

Теорема 1.16. Пусть заданы три точки 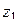, , 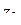 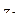на 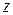-плоскости и три точки 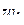, , 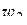 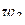на 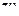-плоскости. Тогда существует един­ственная дробно-линейная функция, переводящая 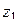, , 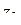 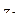соответ­ственно в 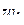, , 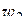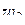. Эта функция определяется формулой

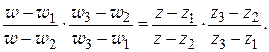                           (1.80)

Доказательство. Находя из (1.80) явное выражение для 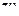, легко убедимся, что (1.80) определяет дробно-линейную функцию 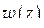. Далее, из (1.80) ясно, что  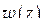переводит точки 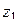, , 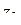 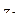соответственно в 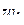, , 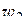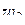. Покажем, что любая дробно-линейная функция, переводящая  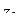в 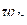, совпадает с построенной. В самом деле, пусть

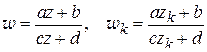 (k = 1, 2, 3);

вычитая почленно из первого и четвертого равенств второе и третье и составляя выражение 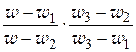, придем к (1.80).

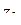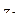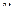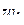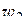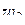Пусть теперь требуется найти конформное и взаимно однозначное отображение круга  на круг  (рис. 1.23). Выберем точки , ,  на границе  круга  и точки , ,  на границе  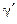круга 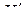 так, чтобы перемещения  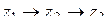и 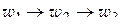 проис­ходили в положительных (относительно , 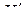) направлениях. Под­ставляя выбранные значения 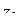,  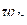в (1.80), получаем дробно-ли­нейную функцию 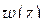, которая отображает  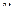на 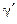 (это следует из кругового свойства и того, что три точки однозначно опреде­ляют окружность); на основании сформулированного выше пра­вила (см. замечание) эта функция конформно и взаимно однозначно отображает круг  на круг .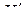

Аналогично может быть получено конформное отображение круга на полуплоскость (и обратно).

Пример. Найти конформное отображение единичного круга 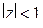 на верхнюю полуплоскость .

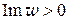Решение. Подставляя в (1.80)

, , ,    , ,

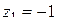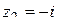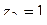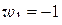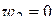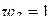
 (рис. 1.24), после преобразований получим дробно-линейную функцию

,

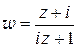переводящую окружность 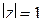 в действительную ось 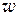-плоскости. Так как в силу выбора точек 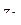, , 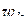обходу окружности  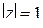в положительном относительно единичного круга направ­лении отвечает обход оси  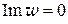в положительном относительно верхней полуплоскости направлении, эта функция дает искомое отображение.

Выбирая другим способом точки 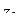 на окружности  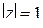и точки  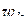на оси 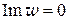, получим другую дробно-линейную функ­цию, решающую ту же задачу. Очевидно, таких функций беско­нечно много; пользуясь (1.80), легко найти общий вид таких функций.