ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ................................................................................................. 4
Раздел 1. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО................................................................................ 6
§ 1.1. Комплексные числа................................................................... 6
§ 1.2. Функции комплексного переменного....................................... 8
§ 1.3. Структура точечных множеств на плоскости........................ 10
§ 1.4. Производная функции комплексного переменного.............. 11
§ 1.5. Аналитические функции. Комплексный потенциал............... 15
§ 1.6. Интеграл от функции комплексного переменного................ 19
§ 1.7. Теорема Коши......................................................................... 23
§ 1.8. Интегральная формула Коши................................................ 27
§ 1.9. Степенные ряды...................................................................... 30
§ 1.10. Некоторые элементарные функции...................................... 34
§ 1.11. Ряд Тейлора.......................................................................... 37
§ 1.12. Ряд Лорана............................................................................ 41
§ 1.13. Изолированные особые точки аналитической функции..... 44
§ 1.14. Вычеты.................................................................................. 46
§ 1.15. Применение вычетов к вычислению несобственных
интегралов............................................................................. 49
§ 1.16. Принцип аргумента.............................................................. 53
§ 1.17. Принцип максимума............................................................. 55
§ 1.18. Понятие о комформном отображении................................. 58
Раздел 2. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ................................................ 67
§ 2.1. Оригинал. L-изображение оригинала.................................... 67
§ 2.2. Свойства преобразования Лапласа........................................ 70
§ 2.3. Таблица некоторых L-изображений...................................... 73
§ 2.4. Восстановление оригинала по его L-изображению............... 74
§ 2.5. Применение операционного исчисления к решению
дифференциальных уравнений............................................... 76
§ 2.6. Применение операционного исчисления
к решению систем дифференциальных уравнений................ 78
§ 2.7. Передаточная функция линейной стационарной цепи.......... 80
§ 2.8. Свертка двух функций. Теорема о свертке............................ 84
§ 2.9. Формула Дюамеля.................................................................. 85
§ 2.10. Дельта-функция. Фильтрующее свойство дельта-функции. 87
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.............................................................. 90
ПРЕДИСЛОВИЕ
Основное назначение данного учебного пособия – методическое обеспечение читаемых студентам всех технических специальностей курсов «Теория автоматического управления», «Математический анализ и теория функций комплексного переменного (ТФКП)». В соответствии с этим пособие состоит из двух разделов: «Элементы ТФКП» и «Операционное исчисление» (такой порядок изложения обусловлен тем, что построение операционного исчисления опирается на методы ТФКП). Содержание разделов соответствует требованиям госстандартов по указанным дисциплинам.
При изложении элементов ТФКП с самого начала внимание читателей обращено на то, что объектом изучения в этой теории является узкий класс функций: аналитические функции комплексного переменного; многочисленные приложения ТФКП к математике и физике связаны с замечательными свойствами этого класса функций. Изложены с подробным обоснованием элементарные основы теории аналитических функций: интегральная теорема и интегральная формула Коши, разложения в ряды Тейлора и Лорана, теорема о вычетах. В качестве приложения вычетов приведено и проиллюстрировано на примерах правило вычисления спектральной плотности сигналов (лемма Жордана). Заключительные параграфы раздела знакомят читателя с базовыми принципами комплексного анализа: принципом аргумента и принципом максимума, лежащими в основе многих приложений ТФКП, и с элементами теории конформных отображений, играющей важную роль в теории краевых задач математической физики.
Изложение раздела «Операционное исчисление» подразделяется на три части (этапа). В первой части (§ 2.1–2.4) излагаются и иллюстрируются на ряде примеров основные понятия и правила операционного исчисления, в том числе удобное правило восстановления оригинала по его лапласовому изображению с помощью вычетов (формула обращения).
Во второй части (§ 2.5, 2.6) этот аппарат применяется к решению задачи Коши для линейных дифференциальных уравнений и систем линейных дифференциальных уравнений с постоянными коэффициентами. Предложен способ решения задачи Коши для линейной системы приведением к стандартному
виду
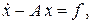
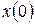 задано
задано
и последующим применением преобразования Лапласа; здесь в построении решения участвует резольвента 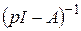 матрицы А системы.
матрицы А системы.
Третья часть (§ 2.7–2.10) посвящена приложению к теории автоматического управления. Вначале вводятся и иллюстрируются на примерах фундаментальные понятия «линейная стационарная цепь (ЛСЦ)», «передаточная функция ЛСЦ», указана связь между передаточной функцией и другим фундаментальным понятием теории ЛСЦ – частотной характеристикой. Затем после проведенной в § 2.8 подготовки (вводится понятие «свертка», доказывается теорема о свертке) выводится широко применяемая в инженерных расчетах формула Дюамеля, представляющая собой удобное правило задания ЛСЦ на языке оригиналов. Заключительный параграф кратко знакомит читателя с дельта-функцией и ее приложением к теории ЛСЦ.
В обоих разделах в конце каждого параграфа приводится задание для самостоятельной работы.
Помимо указанного выше основного назначения учебное пособие может быть использовано при чтении радиотехнических и электротехнических дисциплин, где применяются методы операционного исчисления и ТФКП.
Авторы
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
КОМПЛЕКСНЫЕ ЧИСЛА
В этом параграфе мы напомним читателю простейшие сведения о комплексных числах, используемые в дальнейшем.
Пусть задана прямоугольная система координат на плоскости. Тогда каждое комплексное число 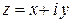 может быть изображено точкой плоскости с координатами
может быть изображено точкой плоскости с координатами 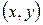 . В частности, действительные числа
. В частности, действительные числа 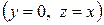 изображаются точками оси абсцисс, называемой поэтому действительной осью; чисто мнимые числа
изображаются точками оси абсцисс, называемой поэтому действительной осью; чисто мнимые числа 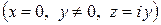 изображаются точками оси ординат, называемой поэтому мнимой осью.
изображаются точками оси ординат, называемой поэтому мнимой осью.
Полярные координаты 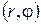 точки (рис. 1.1) называются соответственно модулем и аргументом комплексного числа
точки (рис. 1.1) называются соответственно модулем и аргументом комплексного числа  и обозначаются соответственно
и обозначаются соответственно  ,
, 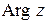 . Очевидно, при
. Очевидно, при 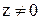
 имеет бесконечно много значений:
имеет бесконечно много значений: 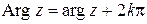
 , где
, где 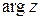 – какое-либо одно из значений
– какое-либо одно из значений 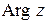 . Условимся в дальнейшем под
. Условимся в дальнейшем под 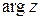 понимать значение
понимать значение 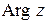 , заключенное в промежутке
, заключенное в промежутке 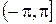 :
:
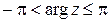 ,
,
и называть его главным значением аргумента  . При
. При  аргумент
аргумент  не определен.
не определен.
Из рис. 1.1 следует
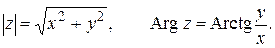
Так как 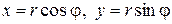 , то
, то
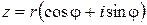 . (1.1)
. (1.1)
Это выражение называют тригонометрической формой комплексного числа  .
.
Пусть имеются два комплексных числа 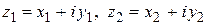 . Тогда
. Тогда
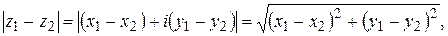
следовательно, модуль разности двух комплексных чисел равен расстоянию между точками, изображающими эти числа. По свойству сторон треугольника (см. рис. 1.2) получаем:
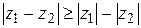 . (1.2)
. (1.2)
Далее имеем
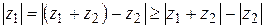 ,
,
откуда
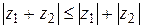 .
.
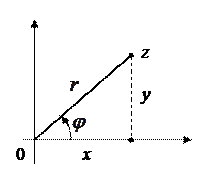
| 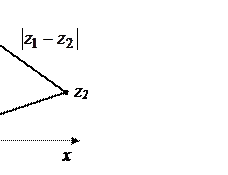
|
Рис. 1.1. Рис. 1.2.
Это неравенство легко распространяется на случай любого числа слагаемых:
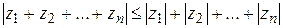 . (1.3)
. (1.3)
Пусть 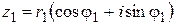 ,
, 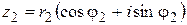 , тогда
, тогда

т. е. при умножении двух комплексных чисел их модули перемножаются, аргументы складываются (и, следовательно, при делении модули делятся, аргументы вычитаются). Отсюда сразу следует формула Муавра:
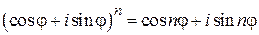 . (1.4)
. (1.4)
Формула (1.4) позволяет получить простое правило извлечения корня п-й степени из комплексного числа. Пусть 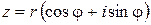 – заданное число,
– заданное число,  – корень п-й степени из
– корень п-й степени из  (т. е.
(т. е.  ). Тогда
). Тогда
 ,
,
откуда 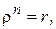
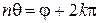 (
( 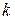 – некоторое целое число). Следовательно, всякий корень п-й степени из
– некоторое целое число). Следовательно, всякий корень п-й степени из  представляется формулой
представляется формулой
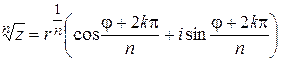 (1.5)
(1.5)
при некотором целом 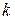 . Подставляя в (1.5) последовательно
. Подставляя в (1.5) последовательно 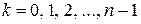 , мы, очевидно, исчерпаем все возможные значения
, мы, очевидно, исчерпаем все возможные значения 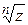 .
.
Пусть 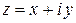 ; тогда комплексное число
; тогда комплексное число 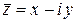 называется сопряженным к
называется сопряженным к  . Числа
. Числа 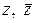 изображаются точками, симметричными относительно действительной оси. В частности, действительные числа (и только они) сопряжены себе. Легко проверяются равенства:
изображаются точками, симметричными относительно действительной оси. В частности, действительные числа (и только они) сопряжены себе. Легко проверяются равенства:
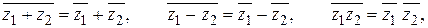
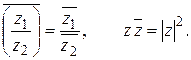
В дальнейшем действительную и мнимую части комплексного числа 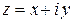 будем обозначать соответственно
будем обозначать соответственно 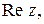
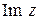 :
:
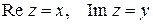 .
.
Очевидны равенства
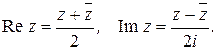
Задание для самостоятельной работы.
1) Найти модуль и аргумент комплексных чисел:
а) 1; б) –3; в) 2i; г) 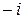 ; д)
; д)  ; е)
; е) 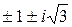 .
.
2) Указать, где расположены точки z, для которых:
а) 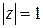 ; б)
; б) 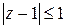 ; в)
; в)  ; г)
; г)  ;
;
д) 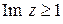 ; е)
; е) 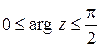 ; ж)
; ж) 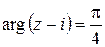 .
.
3) Вычислить:
а) 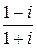 ; б)
; б) 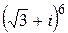 ; в)
; в) 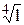 ; г)
; г) 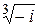 ; д)
; д) 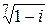 .
.
ТЕОРЕМА КОШИ
В этом параграфе будет установлен фундаментальный факт теории функций комплексного переменного.
Теорема 1.2. Если функция 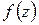 аналитична в односвязной области D, ограниченной замкнутым контуром
аналитична в односвязной области D, ограниченной замкнутым контуром  , а также в точках этого контура, то интеграл от этой функции по контуру
, а также в точках этого контура, то интеграл от этой функции по контуру  равен нулю:
равен нулю:
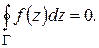
Доказательство. Аналитичность функции 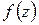 на контуре
на контуре  означает ее дифференцируемость в малых окрестностях точек
означает ее дифференцируемость в малых окрестностях точек  , поэтому функция
, поэтому функция 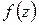 будет дифференцируемой в некоторой области D1, содержащей целиком внутри контур
будет дифференцируемой в некоторой области D1, содержащей целиком внутри контур  и область D (рис. 1.7). Следовательно, ее действительная и мнимая части удовлетворяют в области D1 условиям Коши – Римана
и область D (рис. 1.7). Следовательно, ее действительная и мнимая части удовлетворяют в области D1 условиям Коши – Римана
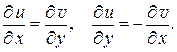
В силу (1.19) имеем:
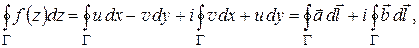
где обозначено
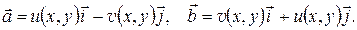
Вычислим роторы векторов 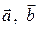 :
:
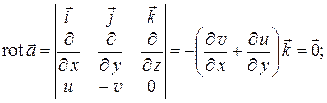
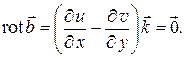

|
Рис. 1.7.
Таким образом, векторы 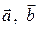 являются потенциальными в односвязной области D1. Следовательно, циркуляция каждого из них по любому замкнутому контуру, лежащему внутри D1 , равна нулю [7]; в частности,
являются потенциальными в односвязной области D1. Следовательно, циркуляция каждого из них по любому замкнутому контуру, лежащему внутри D1 , равна нулю [7]; в частности, 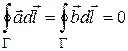 , откуда
, откуда
следует 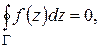 что и требовалось доказать.
что и требовалось доказать.
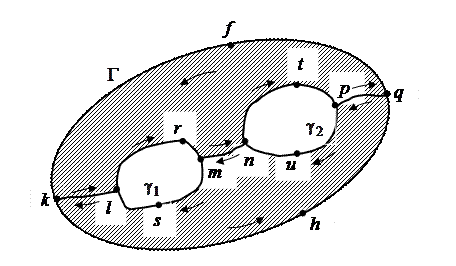
Следствие. Если функция 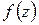 аналитична в многосвязной области D, ограниченной внешним контуром
аналитична в многосвязной области D, ограниченной внешним контуром  и внутренними контурами
и внутренними контурами  (рис. 1.8), а также в точках контуров
(рис. 1.8), а также в точках контуров  ,
,  , то имеет место формула
, то имеет место формула
 (1.23)
(1.23)
В самом деле, пусть, например, внутри контура  (рис. 1.8) лежат два контура
(рис. 1.8) лежат два контура 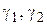 и функция
и функция 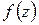 аналитична в трехсвязной области между контуром
аналитична в трехсвязной области между контуром  и контурами
и контурами 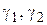 , а также на всех этих контурах.
, а также на всех этих контурах.
|
Рис. 1.8.
Проведем гладкие дуги kl, тп, р q, соединяющие  с
с 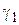 ,
, 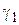 с
с 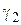 ,
, 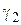 с
с  , и обозначим через
, и обозначим через  замкнутый контур
замкнутый контур 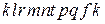 , через
, через  – замкнутый контур
– замкнутый контур  . Тогда в силу теоремы Коши 1.2
. Тогда в силу теоремы Коши 1.2

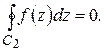
Складывая эти равенства и учитывая, что интегрирование по каждой из дуг kl, тп, р q происходит дважды в противоположных направлениях, получим:

что и требовалось.
Пусть функция 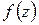 аналитична в односвязной области D. Выберем в области D две точки
аналитична в односвязной области D. Выберем в области D две точки 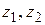 и проведем две дуги
и проведем две дуги 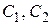 , соединяющие
, соединяющие 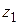 с
с 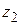 и целиком лежащие в D (рис. 1.9).
и целиком лежащие в D (рис. 1.9).
Тогда из теоремы Коши вытекает:
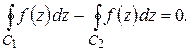
Таким образом, если функция аналитична в односвязной области, то интеграл от нее по любому лежащему в области пути, соединяющему две заданные точки области, одинаков, поэтому имеет смысл обозначение

Рассмотрим интеграл с переменным верхним пределом


|
Рис. 1.9.
Так как
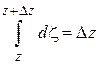
(см. формулу (1.22)), то
 (1.24)
(1.24)
Функция  непрерывна в точке
непрерывна в точке  , поэтому для любого
, поэтому для любого 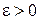 найдется такое
найдется такое 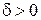 , что при
, что при 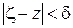 будет
будет 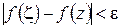 . Выбирая в (1.24)
. Выбирая в (1.24) 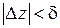 и пользуясь оценкой (1.18) для модуля интеграла, получим:
и пользуясь оценкой (1.18) для модуля интеграла, получим:
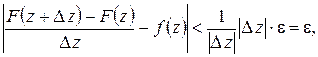
откуда следует
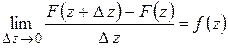 или
или 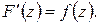
Таким образом, доказано, что функция аналитическая в односвязной области имеет первообразную. Добавим к этому, что любые две первообразные аналитической функции отличаются на постоянную. В самом деле, если 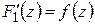 и
и 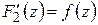 , то, обозначив
, то, обозначив
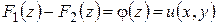 ,
,
получим 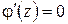 и, следовательно, согласно формуле (1.13)
и, следовательно, согласно формуле (1.13)
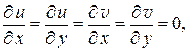
откуда

Из сказанного непосредственно вытекает формула Ньютона – Лейбница для аналитических функций:
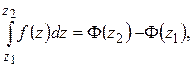
где 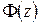 – какая-либо первообразная к
– какая-либо первообразная к 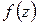 .
.
Задание для самостоятельной работы.
Доказать: если  – замкнутый контур, содержащий внутри точку
– замкнутый контур, содержащий внутри точку  , то
, то
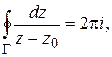
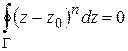
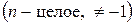 .
.
Вытекает ли последнее равенство из теоремы Коши?
ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
Пусть функция 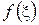 аналитична в односвязной области D, ограниченной замкнутым контуром
аналитична в односвязной области D, ограниченной замкнутым контуром  , и на самом контуре. Зафиксируем в области D точку
, и на самом контуре. Зафиксируем в области D точку 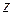 (рис. 1.10) и зададимся произвольным
(рис. 1.10) и зададимся произвольным 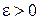 . Так как
. Так как 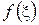 непрерывна в точке
непрерывна в точке 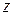 , то найдется такое
, то найдется такое 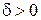 , что во всех точках
, что во всех точках 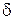 -окрестности точки
-окрестности точки 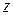 выполняется неравенство
выполняется неравенство
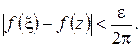
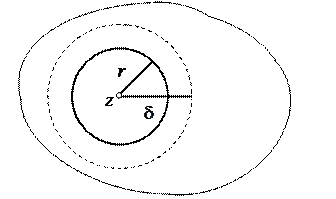
|
Рис. 1.10.
Проведем окружность 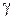 с центром в точке
с центром в точке 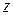 радиуса
радиуса 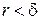 . Пользуясь оценкой (1.18) для модуля интеграла, получим:
. Пользуясь оценкой (1.18) для модуля интеграла, получим:
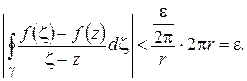
(Здесь учтено, что если 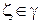 , то
, то 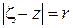 ). Но по следствию из теоремы Коши
). Но по следствию из теоремы Коши
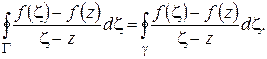
Следовательно,
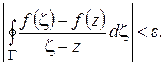
Ввиду произвольности 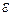 отсюда следует, что
отсюда следует, что
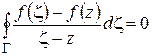
или, что то же,
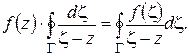
Используя полученный ранее результат (1.21) и деля почленно на 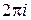 , получим:
, получим:
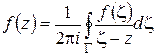 . (1.25)
. (1.25)
Эта формула называется интегральной формулой Коши. Для вычисления интеграла в правой части (он называется интегралом Коши) нужно, очевидно, знать значения функции 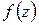 только на контуре
только на контуре  . Таким образом, формула Коши позволяет находить значения аналитической функции внутри области, если известны ее значения на границе области.
. Таким образом, формула Коши позволяет находить значения аналитической функции внутри области, если известны ее значения на границе области.
Замечание 1. Из формулы Коши вытекает: если две функции 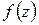 ,
, 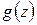 аналитические внутри замкнутого контура
аналитические внутри замкнутого контура  и на самом
и на самом  , имеют одинаковые значения в точках
, имеют одинаковые значения в точках  , то они имеют одинаковые значения и во всех точках внутри
, то они имеют одинаковые значения и во всех точках внутри  . Это утверждение может быть обобщено следующим образом: если две функции, анатилитические в односвязной области D, имеют одинаковые значения на некоторой дуге, лежащей в D, то они совпадают во всей области D. Это замечательное свойство аналитических функций называется свойством единственности.
. Это утверждение может быть обобщено следующим образом: если две функции, анатилитические в односвязной области D, имеют одинаковые значения на некоторой дуге, лежащей в D, то они совпадают во всей области D. Это замечательное свойство аналитических функций называется свойством единственности.
Замечание 2. Если на дуге 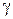 (замкнутой или незамкнутой) задана непрерывная функция
(замкнутой или незамкнутой) задана непрерывная функция 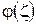 , то выражение
, то выражение
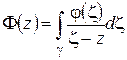 (1.26)
(1.26)
имеет смысл при 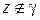 и называется интегралом типа Коши. Из (1.26) следует
и называется интегралом типа Коши. Из (1.26) следует
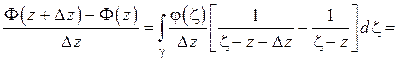
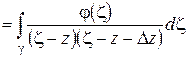 .
.
Предельный переход дает
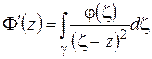 .
.
Аналогично доказывается существование 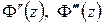 и т. д., при этом
и т. д., при этом
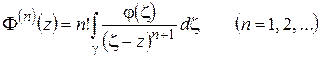 . (1.27)
. (1.27)
Так как интеграл Коши является частным случаем интеграла типа Коши, то из (1.25) и (1.27) вытекает: функция 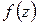 , аналитическая в области D, имеет производные всех порядков в D, при этом
, аналитическая в области D, имеет производные всех порядков в D, при этом
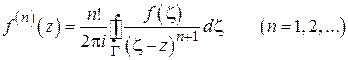 , (1.28)
, (1.28)
где 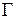 – любой замкнутый контур, содержащий внутри точку z .
– любой замкнутый контур, содержащий внутри точку z .
Доказанная формула (1.25) играет существенную роль в дальнейших исследованиях. Сейчас мы покажем, как эта формула может быть использована для вычисления интегралов.
Пример. Вычислить  , где
, где 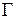 – окружность
– окружность 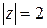 .
.
Решение. Обозначим 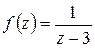 , тогда
, тогда
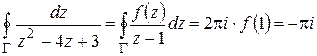
(здесь использовано, что 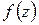 аналитична внутри и на
аналитична внутри и на 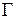 ).
).
Задание для самостоятельной работы.
1) Будет ли верным вычисление, проведенное в последнем примере, если в качестве контура  взять окружность
взять окружность 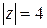 ? Как использовать формулу Коши для вычисления интеграла по такому контуру?
? Как использовать формулу Коши для вычисления интеграла по такому контуру?
2) Вычислить интегралы 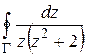 ,
, 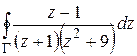 , где
, где 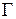 – окружность
– окружность 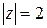 .
.
СТЕПЕННЫЕ РЯДЫ
Определение 1.8. Ряд с комплексными членами
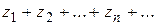 (1.29)
(1.29)
называется сходящимся к числу 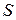 , если последовательность частичных сумм
, если последовательность частичных сумм 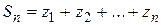 имеет предел, равный
имеет предел, равный 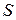 , т. е. если для любого
, т. е. если для любого 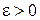 найдется такой номер
найдется такой номер 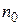 , что при
, что при 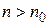 выполняется неравенство
выполняется неравенство 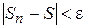 . Число
. Число  называется суммой ряда.
называется суммой ряда.
Обозначим 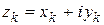 и рассмотрим ряды:
и рассмотрим ряды:
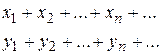 (1.30)
(1.30)
Если ряды (1.30) сходятся соответственно к  то ряд (1.29) сходится к числу
то ряд (1.29) сходится к числу 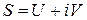 . Обратно, если ряд (1.29) сходится:
. Обратно, если ряд (1.29) сходится: 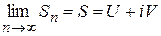 , то
, то  ,
, 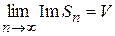 , т. е. ряды (1.30) сходятся. Таким образом, для сходимости ряда (1.29) с комплексными членами необходимо и достаточно, чтобы сходились ряды (1.30), составленные соответственно из действительных и мнимых частей членов этого ряда.
, т. е. ряды (1.30) сходятся. Таким образом, для сходимости ряда (1.29) с комплексными членами необходимо и достаточно, чтобы сходились ряды (1.30), составленные соответственно из действительных и мнимых частей членов этого ряда.
Отсюда, в частности, следует: если ряд с комплексными членами сходится, то его общий член стремится к нулю. В самом деле, из сходимости ряда (1.29) вытекает сходимость рядов (1.30) и, следовательно, стремление 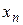 ,
, 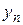 к нулю, откуда следует нужное.
к нулю, откуда следует нужное.
Определение 1.9. Если сходится ряд модулей
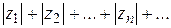 , (1.31)
, (1.31)
то ряд (1.29) называется абсолютно сходящимся.
Абсолютно сходящийся ряд сходится. В самом деле, если 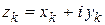 , то
, то 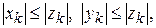 поэтому из сходимости ряда (1.31) вытекает сходимость рядов (1.30), а следовательно, и ряда (1.29).
поэтому из сходимости ряда (1.31) вытекает сходимость рядов (1.30), а следовательно, и ряда (1.29).
Определения и свойства суммы, разности и произведения рядов с действительными членами без изменений переносятся на ряды с комплексными членами.
Рассмотрим комплексный степенной ряд
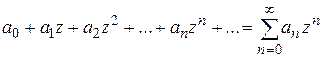 (1.32)
(1.32)
( 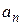 – комплексные числа, называемые коэффициентами ряда,
– комплексные числа, называемые коэффициентами ряда, 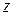 – комплексное переменное).
– комплексное переменное).
Теорема 1.3 (теорема Абеля). Если степенной ряд (1.32) сходится при некотором значении переменного 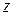 , то он абсолютно сходится при всех значениях
, то он абсолютно сходится при всех значениях 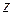 с меньшим модулем.
с меньшим модулем.
Доказательство. Пусть сходится ряд  , тогда последовательность чисел
, тогда последовательность чисел 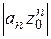 сходится к нулю и, следовательно, ограничена, т. е. найдется такое
сходится к нулю и, следовательно, ограничена, т. е. найдется такое 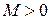 , что
, что
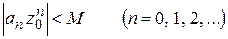 .
.
Если 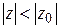 , то число
, то число 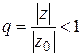 и
и
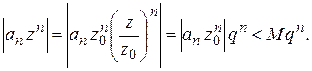
Так как геометрическая прогрессия 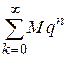 сходится, то на основании теоремы сравнения для рядов с неотрицательными членами ряд
сходится, то на основании теоремы сравнения для рядов с неотрицательными членами ряд 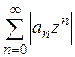 сходится; следовательно, ряд
сходится; следовательно, ряд 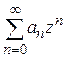 абсолютно сходится, что и требовалось доказать.
абсолютно сходится, что и требовалось доказать.
Замечание. Из теоремы Абеля вытекает: если степенной ряд расходится в точке  , то он расходится при
, то он расходится при  . В самом деле, если бы ряд
. В самом деле, если бы ряд 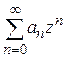 сходился, то по теореме Абеля (так как
сходился, то по теореме Абеля (так как 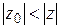 ) ряд
) ряд 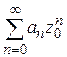 был бы сходящимся, что противоречит условию.
был бы сходящимся, что противоречит условию.
Содержание теоремы Абеля можно не вполне строго выразить так: точки сходимости степенного ряда расположены ближе к нулю, чем любая точка расходимости.
Теорема Абеля позволяет исследовать структуру области сходимости степенного ряда.
В отношении степенного ряда (1.32) возможны три случая:
1) все положительные числа являются точками сходимости;
2) все положительные числа являются точками расходимости;
3) существуют положительные точки сходимости и положительные точки расходимости.
В первом случае по теореме Абеля ряд сходится во всей плоскости. Во втором случае по замечанию к теореме Абеля ряд сходится только в одной точке 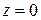 . В третьем случае, так как точки сходимости расположены ближе к нулю, чем точки расходимости, найдется «пограничная» точка
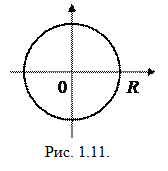
. В третьем случае, так как точки сходимости расположены ближе к нулю, чем точки расходимости, найдется «пограничная» точка 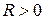 , отделяющая положительные точки сходимости от положительных точек расходимости
, отделяющая положительные точки сходимости от положительных точек расходимости
|
(в самой этой точке ряд может сходиться либо расходиться). Проведем на плоскости круг радиуса  с центром в начале координат (рис. 1.11). Тогда, очевидно, ряд (1.32) будет абсолютно сходиться внутри круга и расходиться вне круга (сходимость или расходимость на границе круга неизвестна).
с центром в начале координат (рис. 1.11). Тогда, очевидно, ряд (1.32) будет абсолютно сходиться внутри круга и расходиться вне круга (сходимость или расходимость на границе круга неизвестна).
Построенный круг называется кругом сходимости степенного ряда (1.32), а его радиус  – радиусом сходимости ряда (1.32). В случаях 1), 2) можно считать соответственно
– радиусом сходимости ряда (1.32). В случаях 1), 2) можно считать соответственно 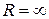 ,
,  . Практическое вычисление радиуса сходимости может быть выполнено с помощью известных признаков сходимости рядов.
. Практическое вычисление радиуса сходимости может быть выполнено с помощью известных признаков сходимости рядов.
Заметим, что ряд
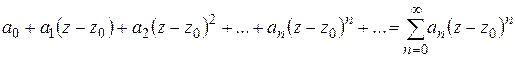 , (1.33)
, (1.33)
где 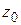 – любое комплексное число, также называется степенным рядом, его областью сходимости является круг с центром в точке
– любое комплексное число, также называется степенным рядом, его областью сходимости является круг с центром в точке 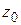 .
.
Рассмотрим круг 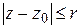 , лежащий внутри круга сходимости ряда (1.33). Тогда числовой ряд
, лежащий внутри круга сходимости ряда (1.33). Тогда числовой ряд
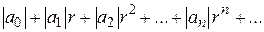
сходится и является мажорантой для ряда (1.33) в круге  , это значит, что
, это значит, что  для всех п.
для всех п.
Определение 1.10. Если для ряда функций
 , (1.34)
, (1.34)
определенных на некотором множестве М, существует сходящаяся числовая мажоранта: при всех 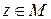
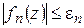
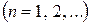 , где
, где 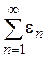 – сходящийся числовой ряд, то будем говорить, что ряд (1.34) правильно сходится на множестве М.
– сходящийся числовой ряд, то будем говорить, что ряд (1.34) правильно сходится на множестве М.
Из сказанного выше вытекает
Лемма 1.1. Степенной ряд (1.33) правильно сходится в любом круге  , лежащем внутри круга сходимости.
, лежащем внутри круга сходимости.
Нам понадобятся следующие два свойства правильно сходящихся рядов.
Теорема 1.4. Если члены ряда (1.34) непрерывны на дуге 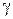 и ряд правильно сходится на
и ряд правильно сходится на 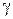 , то и сумма
, то и сумма 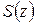 ряда (1.34) непрерывна на
ряда (1.34) непрерывна на 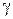 и ряд можно почленно интегрировать по дуге
и ряд можно почленно интегрировать по дуге 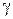 :
:
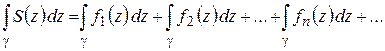 .
.
Теорема 1.5. Если члены ряда (1.34) являются аналитическими функциями в области D и ряд правильно сходится в D, то и сумма 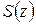 ряда (1.34) является аналитической функцией в области D и ряд (1.34) можно почленно дифференцировать в области D:
ряда (1.34) является аналитической функцией в области D и ряд (1.34) можно почленно дифференцировать в области D:
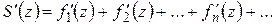 .
.
Первая из этих теорем доказывается так же, как аналогичная теорема для функций действительного переменного. Для доказательства второй выберем окружность 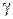 , лежащую вместе с внутренностью в области D, и зафиксируем точку
, лежащую вместе с внутренностью в области D, и зафиксируем точку 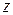 внутри
внутри 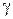 . Тогда при
. Тогда при 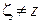 справедливо тождество
справедливо тождество
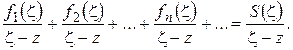 (1.35)
(1.35)
Так как ряд (1.34) имеет в области D сходящуюся числовую мажоранту 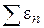 , то ряд (1.35) имеет на
, то ряд (1.35) имеет на 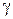 сходящуюся числовую мажоранту
сходящуюся числовую мажоранту 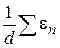
( 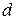 – минимальное расстояние от точек
– минимальное расстояние от точек 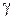 до
до 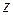 ), т. е. правильно сходится на
), т. е. правильно сходится на 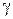 . Интегрируя почленно ряд (1.35) по
. Интегрируя почленно ряд (1.35) по 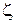 и учитывая, что вследствие аналитичности функций
и учитывая, что вследствие аналитичности функций 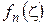 внутри
внутри 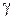 и на
и на 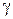 интегралы в левой части могут быть вычислены по формуле Коши (1.25), получим:
интегралы в левой части могут быть вычислены по формуле Коши (1.25), получим:
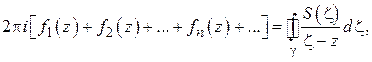
откуда находим:
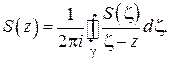
Таким образом, в точках 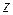 , лежащих внутри
, лежащих внутри 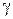 , функция
, функция 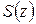 представляется интегралом типа Коши; следовательно (см. § 1.8, замечание 2),
представляется интегралом типа Коши; следовательно (см. § 1.8, замечание 2), 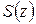 является аналитической функцией внутри
является аналитической функцией внутри 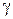 . Так как каждая точка области содержится внутри некоторого круга, лежащего целиком в области, из доказанного вытекает аналитичность
. Так как каждая точка области содержится внутри некоторого круга, лежащего целиком в области, из доказанного вытекает аналитичность 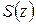 в области D.
в области D.
Аналогично, интегрируя почленно по контуру 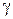 равенство
равенство
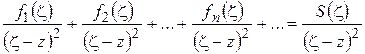
и учитывая формулу (1.28) для производных аналитической функции, получим 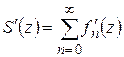 , что и требовалось доказать.
, что и требовалось доказать.
Заметим, что аналогичное утверждение не имеет места для функций действительного переменного: из дифференцируемости членов правильно сходящегося ряда не вытекает дифференцируемость суммы ряда и возможность почленного дифференцирования.
Из леммы 1.1 и теорем 1.4, 1.5 вытекает
Следствие. Сумма степенного ряда (1.33) является аналитической функцией в круге сходимости; степенной ряд можно почленно дифференцировать в круге сходимости и почленно интегрировать по любой дуге, лежащей в круге сходимости.
Задание для самостоятельной работы.
Доказать, что ряд 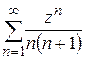 правильно сходится в круге сходимости.
правильно сходится в круге сходимости.
РЯД ТЕЙЛОРА
Рассмотрим функцию 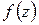 , аналитическую внутри круга
, аналитическую внутри круга 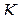 с центром в точке
с центром в точке 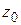 . Покажем, что
. Покажем, что 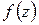 разлагается в этом круге в степенной ряд вида (1.33).
разлагается в этом круге в степенной ряд вида (1.33).
Пусть  – любая точка внутри круга
– любая точка внутри круга 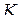 . Проведем внутри
. Проведем внутри 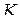 окружность
окружность 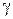 с центром в точке
с центром в точке  так, чтобы точка
так, чтобы точка 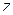 оказалась внутри этой окружности. Тогда значение функции в точке
оказалась внутри этой окружности. Тогда значение функции в точке 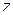 можно представить интегральной формулой Коши:
можно представить интегральной формулой Коши:
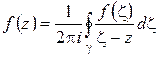 . (1.45)
. (1.45)
Рассмотрим отдельно множитель 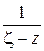 :
:
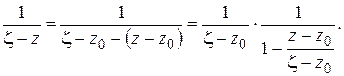 (1.46)
(1.46)
Если точка 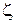 лежит на окружности
лежит на окружности 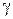 , то
, то 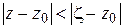 (рис. 1.12), поэтому
(рис. 1.12), поэтому
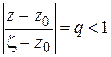
и второй множитель правой части (1.46) является суммой геометрической прогрессии:
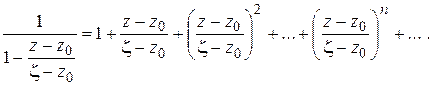 (1.47)
(1.47)

|
Рис. 1.12.
Из (1.46), (1.47) вытекает, что подынтегральную функцию в правой части (1.45) можно представить в виде суммы ряда:
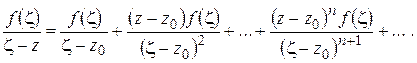 (1.48)
(1.48)
Учитывая, что значения  в точках окружности
в точках окружности  не превосходят некоторой величины М (по свойству непрерывных функций), получим для всех
не превосходят некоторой величины М (по свойству непрерывных функций), получим для всех 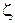 на
на 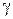 :
:
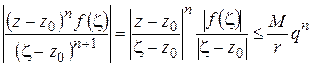
( 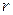 – радиус
– радиус 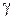 ). Так как числовой ряд
). Так как числовой ряд  сходится (геометрическая прогрессия,
сходится (геометрическая прогрессия,  ), то ряд (1.48) правильно сходится на
), то ряд (1.48) правильно сходится на 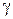 . Подставляя (1.48) в правую часть (1.45) и почленно интегрируя, получим:
. Подставляя (1.48) в правую часть (1.45) и почленно интегрируя, получим:
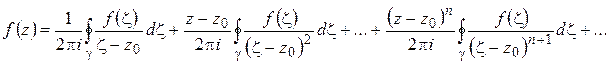
или
 (1.49)
(1.49)
где
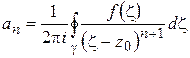 . (1.50)
. (1.50)
Мы представили значение функции в произвольной точке круга 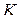 рядом (1.49) с коэффициентами (1.50). Отметим, что коэффициенты (1.50) одни и те же для всех точек
рядом (1.49) с коэффициентами (1.50). Отметим, что коэффициенты (1.50) одни и те же для всех точек  из круга
из круга 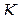 , так как в силу следствия из теоремы Коши величина интеграла (1.50) одна и та же для всех окружностей
, так как в силу следствия из теоремы Коши величина интеграла (1.50) одна и та же для всех окружностей 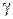 с центром в точке
с центром в точке 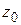 , лежащих внутри круга
, лежащих внутри круга 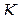 .
.
Ряд (1.49) с коэффициентами (1.50) называется рядом Тейлора. Таким образом, доказана
Теорема 1.8. Любая функция 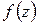 , аналитическая внутри круга с центром
, аналитическая внутри круга с центром 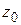 , разлагается внутри этого круга в ряд Тейлора (1.49).
, разлагается внутри этого круга в ряд Тейлора (1.49).
Сопоставляя формулу (1.50) с доказанной формулой (1.28) для производных аналитической функции, получим знакомые выражения для коэффициентов ряда Тейлора:
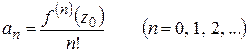 .
.
Замечание 1. Если функция 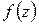 аналитична в точке
аналитична в точке 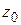 , т. е. дифференцируема в некоторой ее окрестности, то по теореме 1.8 она разлагается в этой окрестности в степенной ряд (1.49). Обратно, если
, т. е. дифференцируема в некоторой ее окрестности, то по теореме 1.8 она разлагается в этой окрестности в степенной ряд (1.49). Обратно, если 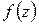 разлагается в степенной ряд в некоторой окрестности точки
разлагается в степенной ряд в некоторой окрестности точки 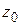 , то по следствию из теоремы 1.5 она аналитична в этой окрестности, а значит, и в точке
, то по следствию из теоремы 1.5 она аналитична в этой окрестности, а значит, и в точке 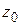 . Таким образом, утверждения «
. Таким образом, утверждения « 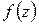 аналитична в точке
аналитична в точке 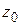 », «
», « 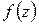 разлагается в степенной ряд в окрестности точки
разлагается в степенной ряд в окрестности точки 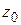 » равносильны. Этим отчасти объясняется термин «аналитическая функция»: она может быть аналитически задана в виде степенного ряда. В дальнейшем читатель должен воспринимать термин «аналитическая функция» как «разлагающаяся в степенной ряд».
» равносильны. Этим отчасти объясняется термин «аналитическая функция»: она может быть аналитически задана в виде степенного ряда. В дальнейшем читатель должен воспринимать термин «аналитическая функция» как «разлагающаяся в степенной ряд».
Замечание 2. Из теоремы 1.8 следует: радиус сходимости ряда Тейлора (1.49) равен расстоянию от точки 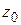 до ближайшей к
до ближайшей к 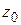 особой точки (т. е. точки, в которой
особой точки (т. е. точки, в которой 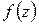 не является аналитической).
не является аналитической).
Замечание 3. Если значения 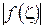 на контуре
на контуре 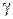 в формуле (1.50) не превосходят числа М, то, пользуясь оценкой (1.18) модуля интеграла, получим:
в формуле (1.50) не превосходят числа М, то, пользуясь оценкой (1.18) модуля интеграла, получим:
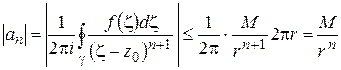
(здесь  – радиус
– радиус 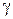 ); таким образом,
); таким образом,
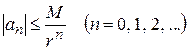 . (1.51)
. (1.51)
Неравенства (1.51) называются неравенствами Коши для коэффициентов ряда Тейлора.
Если 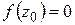 , то точка
, то точка 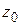 называется нулем функции
называется нулем функции 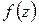 . Предполагая
. Предполагая 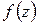 аналитической в точке
аналитической в точке 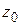 , разложим ее в степенной ряд в окрестности
, разложим ее в степенной ряд в окрестности  ; тогда, очевидно,
; тогда, очевидно,  . Если при этом
. Если при этом 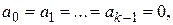
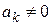 , то число
, то число 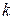 будем называть порядком нуля
будем называть порядком нуля 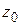 . В этом случае
. В этом случае
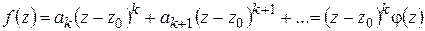 ,
,
где 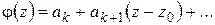 – функция, аналитическая в точке
– функция, аналитическая в точке 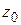 и не равная нулю в этой точке:
и не равная нулю в этой точке: 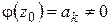 . Обратно, если
. Обратно, если  , где
, где 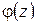 удовлетворяет указанным условиям, то, разложив
удовлетворяет указанным условиям, то, разложив 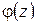 в ряд Тейлора в точке
в ряд Тейлора в точке  , получим:
, получим:
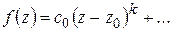 ,
,
где 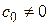 , т. е.
, т. е. 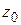 – нуль
– нуль 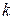 -го порядка
-го порядка 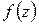 .
.
Например, точки  ,
, 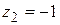 являются нулями первого порядка (или простыми нулями) функции
являются нулями первого порядка (или простыми нулями) функции 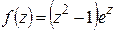 :
: 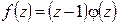 , где
, где 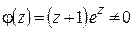 при
при 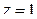 ; аналогично
; аналогично 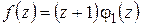 , где
, где 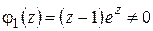 при
при 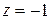 .
.
Задание для самостоятельной работы.
1) Разложить в ряд Тейлора: а) 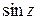 в точке
в точке 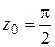 ; б)
; б)  в точке
в точке 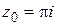 .
.
2) Найти радиус сходимости ряда Тейлора функции 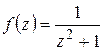 в точке
в точке 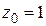 (см. замечание 2).
(см. замечание 2).
3) Найти нули функции и определить их порядки: а) 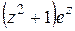 ; б)
; б) 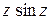 ; в)
; в) 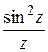 ; г)
; г) 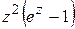 .
.
4) Доказать единственность разложения в ряд Тейлора:
если 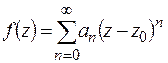 ,
, 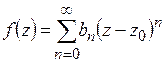 , то
, то 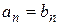
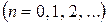 .
.
РЯД ЛОРАНА
Рассмотрим функцию 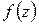 , аналитическую внутри кольца между двумя окружностями с центром
, аналитическую внутри кольца между двумя окружностями с центром 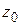 (в частном случае кольцо может быть кругом с «выколотым» центром). Проведем окружности
(в частном случае кольцо может быть кругом с «выколотым» центром). Проведем окружности 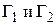 с центром в точке
с центром в точке 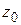 так, чтобы каждая из них находилась внутри данного кольца и чтобы точка
так, чтобы каждая из них находилась внутри данного кольца и чтобы точка  оказалась между ними. Из точки
оказалась между ними. Из точки 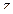 как из центра проведем окружность
как из центра проведем окружность 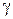 , лежащую между
, лежащую между 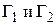 (рис. 1.13).
(рис. 1.13).

|
Рис. 1.13.
В силу следствия из теоремы Коши имеем:
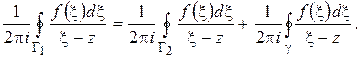
На основании интегральной формулы Коши последний из этих трех интегралов равен  , поэтому получаем:
, поэтому получаем:
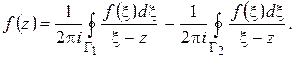 (1.52)
(1.52)
Первое слагаемое правой части на основании вычислений § 1.11 представляется рядом
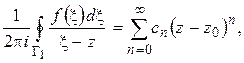
где
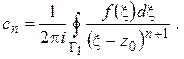 (1.53)
(1.53)
Чтобы разложить в ряд второе слагаемое, заметим, что если  , то
, то  , поэтому
, поэтому
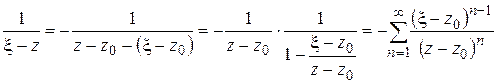 ,
,
откуда
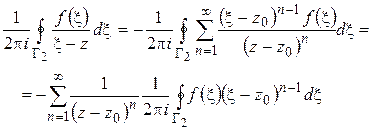
или
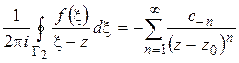 ,
,
где
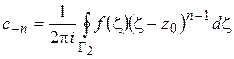 (1.54)
(1.54)
(возможность почленного интегрирования проверяется так же, как в предыдущем параграфе). Заметим, что в формулах (1.53), (1.54) в качестве контура интегрирования можно взять любую окружность  с центром в точке
с центром в точке 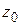 , лежащую внутри кольца (по следствию из теоремы Коши), поэтому формулы (1.53), (1.54) можно объединить в одну следующим образом:
, лежащую внутри кольца (по следствию из теоремы Коши), поэтому формулы (1.53), (1.54) можно объединить в одну следующим образом:
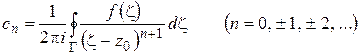 . (1.55)
. (1.55)
Подставляя полученные разложения в (1.52), получим:
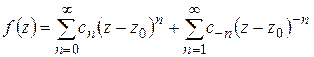
или
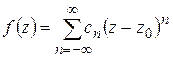 (1.56)
(1.56)
с коэффициентами (1.55).
Ряд (1.56) называется рядом Лорана.
Таким образом, доказана
Теорема 1.9. Любая функция  , аналитическая внутри кольца с центром
, аналитическая внутри кольца с центром  , разлагается внутри этого кольца в ряд Лорана (1.56) с коэффициентами (1.55).
, разлагается внутри этого кольца в ряд Лорана (1.56) с коэффициентами (1.55).
Пример. Разложить функцию  в ряд Лорана в кольце
в ряд Лорана в кольце 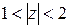 .
.
Решение. Вначале разложим  на простейшие дроби:
на простейшие дроби:
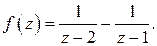
Разложим в ряд каждое слагаемое отдельно, используя примененный выше прием: разложение в бесконечно убывающую геометрическую прогрессию. Так как в данном кольце 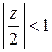 ,
, 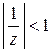 , то
, то
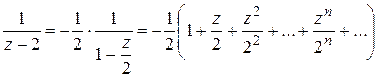 ;
;
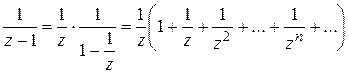 .
.
Вычитая эти разложения, получим:
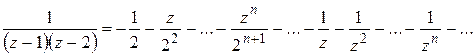
Замечание. Если в формуле (1.55) значения 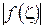 на контуре
на контуре  не превосходят числа М и радиус
не превосходят числа М и радиус  равен
равен 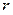 , то, повторяя вычисления, проведенные в § 1.11 (замечание 3), получим оценки для модулей коэффициентов ряда Лорана:
, то, повторяя вычисления, проведенные в § 1.11 (замечание 3), получим оценки для модулей коэффициентов ряда Лорана:
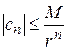 (
( 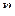 = 0, ±1, ±2, …).
= 0, ±1, ±2, …).
Задание для самостоятельной работы.
1) Разложить в ряд Лорана: а) 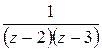 в кольце
в кольце 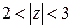 и в кольце
и в кольце 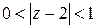 ; б)
; б) 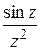 в кольце
в кольце 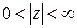 .
.
2) Доказать единственность разложения в ряд Лорана:
если 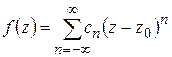 и
и 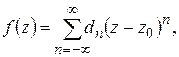
то 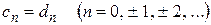 .
.
§ 1.13. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
АНАЛИТИЧЕСКОЙ ФУНКЦИИ
Точки плоскости, в которых функция 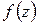 является аналитической, будем называть правильными точками этой функции, а точки, в которых
является аналитической, будем называть правильными точками этой функции, а точки, в которых  не является аналитической (в частности, точки, в которых
не является аналитической (в частности, точки, в которых  не определена), – особыми точками. Особая точка называется изолированной, если в некоторой ее окрестности нет других особых точек.
не определена), – особыми точками. Особая точка называется изолированной, если в некоторой ее окрестности нет других особых точек.
Если 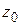 есть изолированная особая точка
есть изолированная особая точка 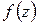 , то в достаточно малом круге с «выколотым» центром
, то в достаточно малом круге с «выколотым» центром  функция
функция  будет аналитической и, следовательно, разлагается в ряд Лорана
будет аналитической и, следовательно, разлагается в ряд Лорана
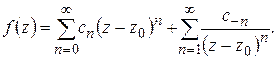 (1.57)
(1.57)
Ряд 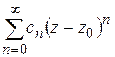 назовем правильной частью, ряд
назовем правильной частью, ряд 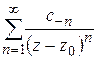 – главной частью разложения (1.57). Возможны три случая:
– главной частью разложения (1.57). Возможны три случая:
1) В разложении (1.57) отсутствует главная часть (т. е. все коэффициенты  ).
).
2) Главная часть содержит конечное число членов.
3) Главная часть содержит бесконечное число членов.
В этих случаях особая точка  называется соответственно 1) устранимой, 2) полюсом, 3) существенно особой точкой.
называется соответственно 1) устранимой, 2) полюсом, 3) существенно особой точкой.
В случае устранимой особой точки из (1.57) следует 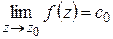 . Если доопределить
. Если доопределить  в точке
в точке 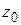 , приняв
, приняв  , то
, то  станет правильной точкой
станет правильной точкой 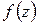 (особенность «устраняется»).
(особенность «устраняется»).
Если 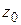 – полюс, то
– полюс, то
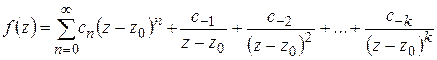 , (1.58)
, (1.58)
где 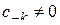 .
.
После приведения к общему знаменателю получим:
 , (1.59)
, (1.59)
где обозначено:
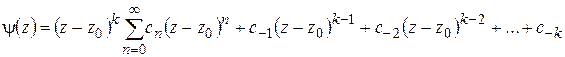 .
.
Последнее равенство показывает, что функция 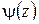 является аналитичес-кой в точке
является аналитичес-кой в точке 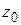 и
и 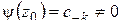 .
.
Таким образом, если точка 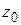 является полюсом функции
является полюсом функции 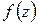 , то в окрестности этой точки
, то в окрестности этой точки 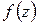 изображается в виде (1.59), где
изображается в виде (1.59), где 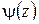 аналитична в точке
аналитична в точке  и
и 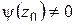 . Обратно, если
. Обратно, если 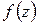 имеет вид (1.59), где
имеет вид (1.59), где 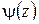 удовлетворяет указанным условиям, то, разлагая
удовлетворяет указанным условиям, то, разлагая 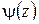 в ряд Тейлора в точке
в ряд Тейлора в точке  и выполняя почленное деление на
и выполняя почленное деление на 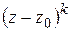 , получим разложение вида (1.58), откуда следует, что
, получим разложение вида (1.58), откуда следует, что 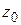 – полюс
– полюс  .
.
Число 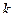 называется порядком полюса. Полюс первого порядка называется простым полюсом.
называется порядком полюса. Полюс первого порядка называется простым полюсом.
Заметим следующее: функция 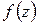 имеет в точке
имеет в точке  полюс
полюс 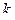 -го порядка тогда и только тогда, если функция
-го порядка тогда и только тогда, если функция 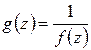 имеет в точке
имеет в точке 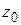 нуль такого же порядка (см. конец § 1.11). В самом деле, из (1.59) (с выполнением указанных условий для
нуль такого же порядка (см. конец § 1.11). В самом деле, из (1.59) (с выполнением указанных условий для 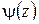 ) следует:
) следует:
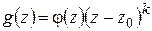 ,
,
где 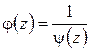 аналитична и не равна нулю в точке
аналитична и не равна нулю в точке 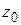 , т. е.
, т. е.  является нулем
является нулем 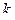 -го порядка для
-го порядка для 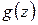 ; обратный переход выполняется так же.
; обратный переход выполняется так же.
Из формулы (1.59) вытекает:
если 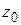 – полюс
– полюс  , то
, то
 .
.
Таким образом, поведение аналитической функции в окрестности полюса может быть описано следующим образом: при стремлении к  по любому направлению
по любому направлению  .
.
Чтобы выяснить поведение функции в окрестности существенно особой точки, рассмотрим следующий пример. Пусть 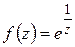 . Тогда из формулы (1.36) вытекает:
. Тогда из формулы (1.36) вытекает:
при 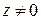
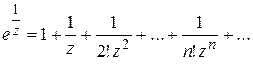 (1.60)
(1.60)
Так как это разложение содержит бесконечно много членов с отрицательными степенями  , то точка является существенно особой точкой для
, то точка является существенно особой точкой для 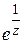 . Обратим внимание на следующее: если
. Обратим внимание на следующее: если  стремится к нулю слева (
стремится к нулю слева ( 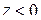 ), то
), то 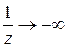 и
и 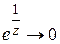 ; если
; если 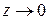 справа (
справа ( 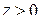 ), то
), то 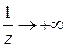 и
и 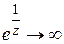 . Эти элементарные соображения показывают, что поведение функции в окрестности существенно особой точки более сложно, чем в окрестности устранимой особой точки и полюса. Можно доказать, что справедлива следующая теорема Сохоцкого: если
. Эти элементарные соображения показывают, что поведение функции в окрестности существенно особой точки более сложно, чем в окрестности устранимой особой точки и полюса. Можно доказать, что справедлива следующая теорема Сохоцкого: если 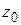 – существенно особая точка аналитической функции
– существенно особая точка аналитической функции  , то для любого комплексного числа
, то для любого комплексного числа 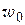 найдется последовательность точек
найдется последовательность точек 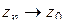 такая, что
такая, что  .
.
Задание для самостоятельной работы.
1) Найти особые точки функции и определить их характер (для полюсов указать их порядки):
а)  ; б)
; б) 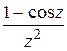 ; в)
; в) 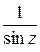 ; г)
; г) 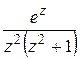 ; д)
; д) 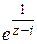 .
.
2) Будет ли точка  изолированной особой точкой для функции
изолированной особой точкой для функции 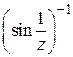 ?
?
ВЫЧЕТЫ
Пусть 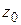 – изолированная особая точка аналитической функции
– изолированная особая точка аналитической функции  ; тогда в окрестности этой точки
; тогда в окрестности этой точки  изобразится рядом Лорана (1.57).
изобразится рядом Лорана (1.57).
Определение 1.11. Коэффициент при 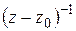 в разложении Лорана (1.57), т. е. число
в разложении Лорана (1.57), т. е. число 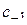 называется вычетом функции
называется вычетом функции  относительно особой точки
относительно особой точки 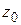 и обозначается
и обозначается 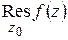 :
:
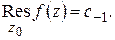
Например, из (1.60) вытекает:  .
.
Из формулы (1.55) для коэффициентов ряда Лорана следует:
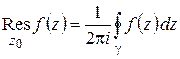 , (1.61)
, (1.61)
где 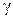 – окружность с центром
– окружность с центром 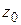 достаточно малого радиуса.
достаточно малого радиуса.
Роль вычетов выясняет следующая
Теорема 1.10 (основная теорема о вычетах). Если функция 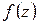 аналитична внутри замкнутого контура
аналитична внутри замкнутого контура  и на самом контуре, за исключением конечного числа точек
и на самом контуре, за исключением конечного числа точек 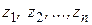 внутри
внутри  , то интеграл
, то интеграл 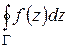 равен произведению числа
равен произведению числа 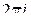 на сумму вычетов относительно особых точек, лежащих внутри
на сумму вычетов относительно особых точек, лежащих внутри  :
:
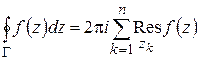 . (1.62)
. (1.62)
Доказательство. Проведем окружности 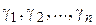 с центрами соответственно
с центрами соответственно 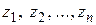 столь малых радиусов, чтобы все окружности лежали внутри
столь малых радиусов, чтобы все окружности лежали внутри  , не имели общих точек и внутри каждой окружности находилась только одна особая точка (рис. 1.14). Тогда в силу следствия из теоремы Коши
, не имели общих точек и внутри каждой окружности находилась только одна особая точка (рис. 1.14). Тогда в силу следствия из теоремы Коши
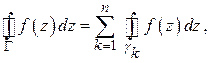
откуда, вследствие (1.61), и вытекает формула (1.62).
 
|
Рис. 1.14.
Доказанная теорема показывает: если мы научимся практически находить вычеты, то это даст нам подход к вычислению интегралов от функций комплексного переменного. Укажем некоторые приемы вычисления вычетов.
1) Пусть 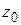 – простой полюс
– простой полюс 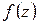 :
:
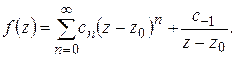
Умножая почленно на 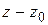 и переходя к пределу при
и переходя к пределу при 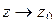 , получим:
, получим:
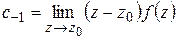 . (1.63)
. (1.63)
Пусть теперь 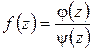 , где
, где 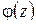 ,
, 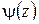 аналитичны в точке
аналитичны в точке 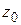 и
и 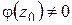 ,
, 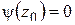 ,
, 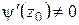 . Последнее условие означает, что
. Последнее условие означает, что  является простым нулем
является простым нулем 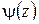 и, следовательно, простым полюсом для
и, следовательно, простым полюсом для 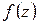 . Формула (1.63) дает:
. Формула (1.63) дает:
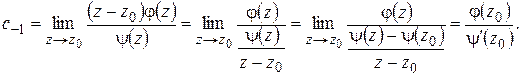
Итак, в этом случае
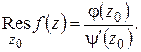 (1.64)
(1.64)
Например, 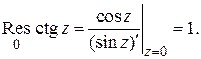
2) Пусть  – полюс второго порядка
– полюс второго порядка  :
:
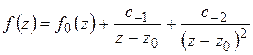 ,
,
где 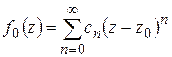 . Умножая почленно на
. Умножая почленно на 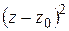 и дифференцируя полученное равенство по
и дифференцируя полученное равенство по  , получим:
, получим:
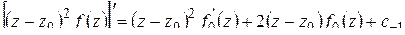 ,
,
откуда
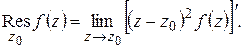
Например,
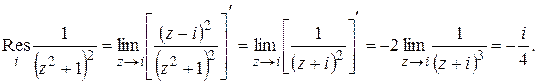 (*)
(*)
Аналогичным вычислением может быть найден вычет относительно полюса
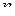 -го порядка:
-го порядка:
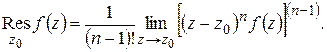 (1.65)
(1.65)
3) В ряде случаев вычет может быть найден путем разложения в ряд Лорана.
Пример 1. Найти 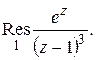
Решение. Имеем:
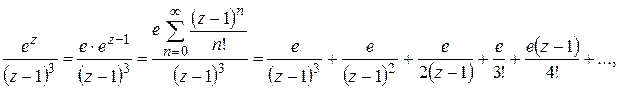
откуда 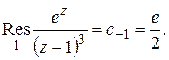
Пример 2. Вычислить  , где Г – окружность
, где Г – окружность 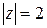 .
.
Решение. Оба полюса 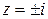 лежат внутри Г, поэтому, применяя формулы (1.62), (1.64), получим:
лежат внутри Г, поэтому, применяя формулы (1.62), (1.64), получим:
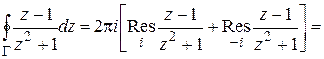
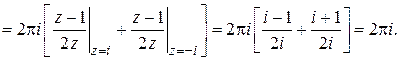
Задание для самостоятельной работы.
1) Найти вычеты следующих функций относительно каждого из полюсов:
а) 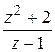 ; б)
; б) 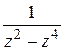 ; в)
; в) 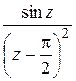 ; г)
; г) 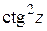 ; д)
; д) 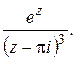
2) Вычислить  , где Г – окружность
, где Г – окружность 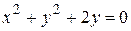 .
.
§ 1.15. ПРИМЕНЕНИЕ ВЫЧЕТОВ
К ВЫЧИСЛЕНИЮ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
С помощью вычетов могут быть вычислены некоторые несобственные интегралы от функций действительного переменного.
Теорема 1.11. Если функция  аналитична на действительной оси и в верхней полуплоскости, за исключением конечного числа точек
аналитична на действительной оси и в верхней полуплоскости, за исключением конечного числа точек 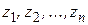
в верхней полуплоскости, и если  при
при 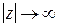 стремится к нулю быстрее, чем
стремится к нулю быстрее, чем  :
:
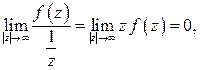 (1.66)
(1.66)
то
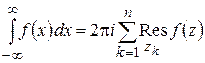 . (1.67)
. (1.67)
Доказательство. При достаточно большом  все особые точки
все особые точки 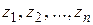 будут лежать внутри полукруга, ограниченного сегментом
будут лежать внутри полукруга, ограниченного сегментом 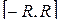 и верхней половиной
и верхней половиной 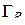 окружности
окружности 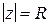 (рис. 1.15). Тогда в силу основной теоремы о вычетах
(рис. 1.15). Тогда в силу основной теоремы о вычетах
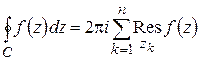 (1.68)
(1.68)
(С – граница полукруга); с другой стороны,
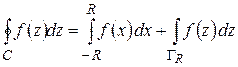 .
.

|
Рис. 1.15.
Заменяя левую часть величиной (1.68) и переходя к пределу при 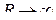 , получим:
, получим:
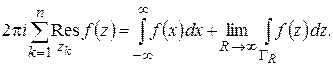
Остается показать, что последний предел равен нулю. Зададимся произвольным 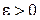 . Тогда по условию (1.66) существует такое
. Тогда по условию (1.66) существует такое 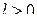 , что при
, что при 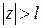 будет
будет  . Но
. Но 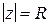 в точках полуокружности
в точках полуокружности 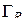 ; следовательно, если взять
; следовательно, если взять 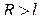 , то при
, то при 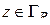 будет:
будет:
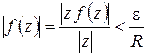 ;
;
тогда в силу (1.18)
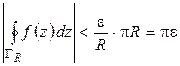 .
.
Таким образом, показано, что, выбирая радиус 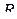 полуокружности
полуокружности 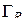 достаточно большим, мы можем сделать величину
достаточно большим, мы можем сделать величину 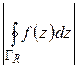 сколь угодно малой, а это и значит, что
сколь угодно малой, а это и значит, что 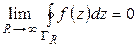 . Теорема доказана.
. Теорема доказана.
Пример 1. Вычислить
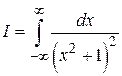 .
.
Решение. Функция 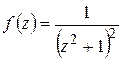 аналитична на действительной оси, имеет в верхней полуплоскости только одну особую точку
аналитична на действительной оси, имеет в верхней полуплоскости только одну особую точку 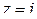 и удовлетворяет условию (1.66).
и удовлетворяет условию (1.66).
Следовательно, применяя формулу (1.67) и используя ранее полученный результат (*), находим:
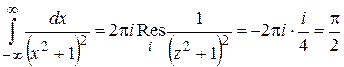 .
.
При вычислении несобственных интегралов иногда бывает полезна следующая лемма (приводим ее без доказательства):
Лемма Жордана. Если функция  имеет вид:
имеет вид:
 , (1.69)
, (1.69)
где 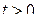 ,
, 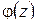 аналитична на действительной оси и в верхней полуплоскости, за исключением конечного числа точек
аналитична на действительной оси и в верхней полуплоскости, за исключением конечного числа точек  , и
, и 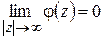 , то имеет место формула (1.67).
, то имеет место формула (1.67).
Пример 2. Вычислить
 .
.
Решение. Обратим внимание, что для этого интеграла условие (1.66) не выполняется. Далее заметим, что
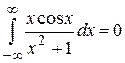
(так как функция 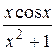 нечетная). Поэтому
нечетная). Поэтому
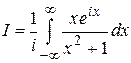 .
.
Подынтегральная функция имеет вид (1.69):  ,
,  – аналитична на действительной оси, имеет в верхней полуплоскости полюс
– аналитична на действительной оси, имеет в верхней полуплоскости полюс  ,
, 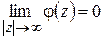 . Поэтому на основании леммы Жордана и формулы (1.64)
. Поэтому на основании леммы Жордана и формулы (1.64)
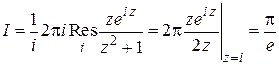 .
.
В заключение этого параграфа рассмотрим пример на вычисление несобственного интеграла с использованием теоремы Коши (теорема 1.2).
Пример 3. Вычислить интеграл Пуассона 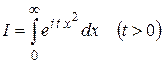 .
.
Решение. Функция 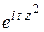 аналитична во всей плоскости, поэтому в силу теоремы Коши интеграл от нее по границе сектора ОАВ (рис. 1.16) равен нулю:
аналитична во всей плоскости, поэтому в силу теоремы Коши интеграл от нее по границе сектора ОАВ (рис. 1.16) равен нулю:
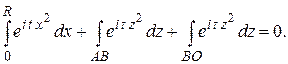
Переходя к пределу при  , получим
, получим 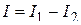 , где
, где


|
Рис. 1.16.
На отрезке 
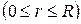 , поэтому
, поэтому
 .
.
(Здесь использовано, что 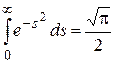 ). На дуге
). На дуге 
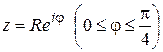 , поэтому
, поэтому
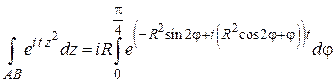 .
.
Откуда, учитывая неравенство  , получим
, получим
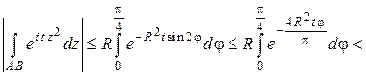
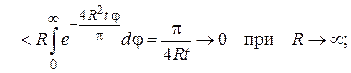
следовательно,  . Таким образом
. Таким образом
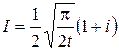 .
.
ПРИНЦИП АРГУМЕНТА
Укажем правило подсчета числа нулей и полюсов аналитической функции внутри заданного контура.
Теорема 1.12. Пусть функция 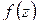 не имеет нулей и особых точек на замкнутом контуре
не имеет нулей и особых точек на замкнутом контуре  и имеет внутри
и имеет внутри  конечное число особых точек, являющихся полюсами. Тогда разность между числом нулей и числом полюсов функции
конечное число особых точек, являющихся полюсами. Тогда разность между числом нулей и числом полюсов функции 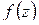 внутри контура
внутри контура  равна числу оборотов, которые описывает вектор, соединяющий начало координат с точкой
равна числу оборотов, которые описывает вектор, соединяющий начало координат с точкой 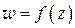 , при однократном обходе точкой
, при однократном обходе точкой  контура
контура  в положительном направлении (при этом каждый нуль и каждый полюс засчитывается столько раз, какова их кратность).
в положительном направлении (при этом каждый нуль и каждый полюс засчитывается столько раз, какова их кратность).
Доказательство. Напомним: если точка 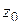 – нуль порядка
– нуль порядка 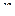 функции
функции 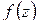 , то в окрестности точки
, то в окрестности точки 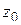
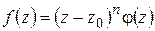 , (1.70)
, (1.70)
где 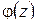 аналитична в точке
аналитична в точке 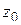 и
и 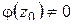 . Из (1.70) вытекает:
. Из (1.70) вытекает:

и
 .
.
Функция 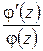 аналитична в точке
аналитична в точке  ; следовательно, функция
; следовательно, функция  имеет простой полюс в точке
имеет простой полюс в точке 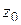 и
и
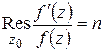 .
.
Аналогично, если 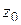 – полюс порядка m функции
– полюс порядка m функции 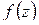 , то в окрестности
, то в окрестности 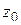
 ,
,
где 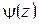 аналитична в точке
аналитична в точке 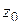 и
и 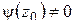 . Повторяя вычисления, получим:
. Повторяя вычисления, получим:
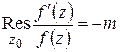 .
.
Так как на  нет нулей и полюсов
нет нулей и полюсов 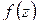 , то функция
, то функция 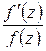 аналитична на
аналитична на  . Обозначая нули и полюса
. Обозначая нули и полюса 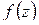 внутри
внутри  соответственно через
соответственно через 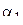 , …,
, …, 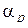 ,
, 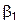 , …,
, …, 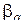 , по основной теореме о вычетах получим:
, по основной теореме о вычетах получим:
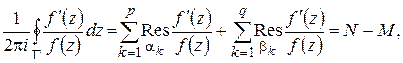 (1.71)
(1.71)
где N – сумма кратностей нулей 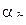 , M – сумма кратностей полюсов
, M – сумма кратностей полюсов  . С другой стороны, учитывая, что
. С другой стороны, учитывая, что 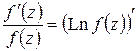 , по формуле Ньютона – Лейбница для аналитических функций (см. § 1.7) имеем:
, по формуле Ньютона – Лейбница для аналитических функций (см. § 1.7) имеем:
 ,
,
где правая часть означает приращение, которое получает 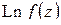 , когда точка
, когда точка  описывает контур
описывает контур  в положительном направлении. Так как
в положительном направлении. Так как
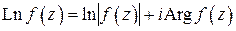 ,
,
то
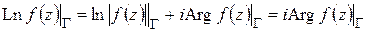
(функция 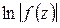 непрерывна на
непрерывна на  и после обхода возвращается к первоначальному значению) и
и после обхода возвращается к первоначальному значению) и
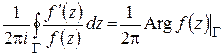 .
.
Правая часть этого равенства выражает число оборотов, которые описывает вектор, соединяющий начало координат с точкой 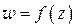 , когда точка
, когда точка  описывает
описывает  в положительном направлении. Сопоставляя с (1.71), получим:
в положительном направлении. Сопоставляя с (1.71), получим:
 ,
,
что и требовалось доказать.
Доказанное правило называется принципом аргумента. Очевидно, в частном случае, если внутри  нет полюсов
нет полюсов 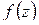 , принцип аргумента дает возможность подсчитать число нулей
, принцип аргумента дает возможность подсчитать число нулей 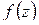 внутри
внутри  .
.
Пример. Доказать, что многочлен степени п
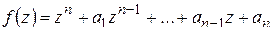
имеет ровно п нулей.
Решение. Имеем
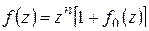 , (1.72)
, (1.72)
где
 .
.
Так как 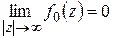 , то существует такое
, то существует такое  , что при
, что при 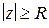 будет
будет 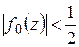 ; следовательно, точка, изображающая
; следовательно, точка, изображающая 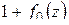 , будет лежать внутри круга радиуса
, будет лежать внутри круга радиуса 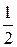 с центром в точке
с центром в точке  (рис. 1.17). Из сказанного вытекает, что: а) все нули
(рис. 1.17). Из сказанного вытекает, что: а) все нули 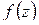 лежат внутри окружности
лежат внутри окружности 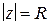 ; б) когда точка
; б) когда точка  описывает окружность
описывает окружность 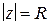 в положительном направлении, точка
в положительном направлении, точка 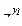 (первый множитель в (1.72)) делает п полных оборотов вокруг нуля, точка
(первый множитель в (1.72)) делает п полных оборотов вокруг нуля, точка 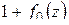 (второй множитель (1.72)) – ни одного; следовательно, точка
(второй множитель (1.72)) – ни одного; следовательно, точка  делает п полных оборотов. В силу принципа аргумента число нулей
делает п полных оборотов. В силу принципа аргумента число нулей 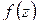 равно n, что и требовалось доказать.
равно n, что и требовалось доказать.

|
Рис. 1.17.
Доказанное утверждение называется основной теоремой алгебры.
ПРИНЦИП МАКСИМУМА
Применим принцип аргумента для обоснования другого фундаменталь-ного правила теории функций – принципа максимума. Сначала докажем следующую лемму.
Лемма 1.2. Если функция 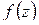 аналитична в точке
аналитична в точке 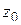 ,
, 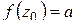 ,
, 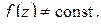 то существует окрестность точки
то существует окрестность точки 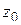 , не содержащая корней уравнения
, не содержащая корней уравнения 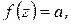 кроме точки
кроме точки 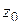 .
.
Доказательство. Так как 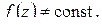 то в разложении Тейлора
то в разложении Тейлора 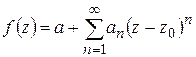 хотя бы одно из чисел
хотя бы одно из чисел 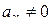 , поэтому имеем:
, поэтому имеем:
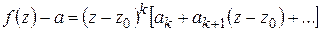 , (1.73)
, (1.73)
где 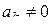 . С другой стороны, если в любой близости точки
. С другой стороны, если в любой близости точки 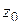 имелись бы корни уравнения
имелись бы корни уравнения 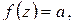 то существовала бы последовательность точек
то существовала бы последовательность точек 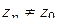 ,
, 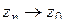 ,
, 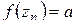 . Подставляя в (1.73)
. Подставляя в (1.73) 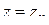 и учитывая, что
и учитывая, что 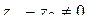 , получили бы
, получили бы
 ;
;
переходя к пределу при  , получили бы
, получили бы 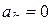 . Полученное противоречие доказывает лемму.
. Полученное противоречие доказывает лемму.
Теорема 1.13 (принцип максимума). Если функция 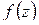 , не равная постоянной, непрерывна в ограниченной замкнутой области
, не равная постоянной, непрерывна в ограниченной замкнутой области 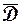 и аналитична во внутренних точках
и аналитична во внутренних точках 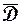 , то ее модуль достигает наибольшего значения на границе области
, то ее модуль достигает наибольшего значения на границе области 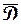 .
.
Доказательство. Так как функция 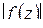 непрерывна в замкнутой ограниченной области
непрерывна в замкнутой ограниченной области 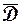 , то она достигает наибольшего значения в некоторой точке
, то она достигает наибольшего значения в некоторой точке 
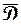 :
:
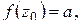
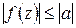 при
при 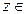
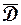 . (1.74)
. (1.74)
Геометрически это означает, что все точки  при
при 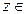
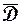 лежат в круге
лежат в круге 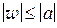 на
на 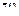 -плоскости (рис. 1.19). Покажем, что
-плоскости (рис. 1.19). Покажем, что 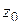 – граничная точка
– граничная точка 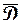 .
.
В самом деле, пусть 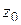 – внутренняя точка
– внутренняя точка 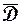 . Тогда
. Тогда 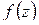 удовлетворяет в точке
удовлетворяет в точке 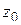 условиям леммы 1.2, и поэтому существует столь малая окружность
условиям леммы 1.2, и поэтому существует столь малая окружность 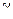 с центром
с центром 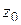 , что на
, что на 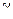 и внутри
и внутри 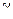 нет нулей функции
нет нулей функции  кроме точки
кроме точки 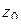 (можно считать, что
(можно считать, что 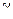 с внутренностью целиком лежит внутри
с внутренностью целиком лежит внутри 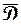 (рис. 1.18)). Обозначив
(рис. 1.18)). Обозначив 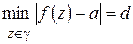 (очевидно,
(очевидно, 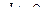 ) и выбрав точку
) и выбрав точку 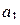 так, что
так, что  ,
, 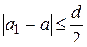 (рис. 1.19), будем иметь:
(рис. 1.19), будем иметь:
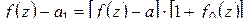 ,
,
где
 ,
, 
при 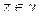 .
.
При обходе точкой  окружности
окружности 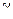 в положительном направлении первый множитель в правой части делает не менее одного оборота вокруг нуля (в силу принципа аргумента), второй – ни одного (рис. 1.17), следовательно, функция
в положительном направлении первый множитель в правой части делает не менее одного оборота вокруг нуля (в силу принципа аргумента), второй – ни одного (рис. 1.17), следовательно, функция 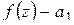 имеет хотя бы один нуль
имеет хотя бы один нуль 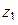 внутри
внутри 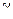 :
: 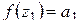 . Получено противоречие с (1.74), теорема доказана.
. Получено противоречие с (1.74), теорема доказана.
Теорема 1.14. Функция 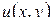 , гармоническая в замкнутой ограниченной области
, гармоническая в замкнутой ограниченной области  и не равная постоянной, достигает наибольшего и наименьшего значения на границе области
и не равная постоянной, достигает наибольшего и наименьшего значения на границе области 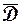 .
.
Доказательство. Обозначим 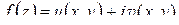 , где
, где  – гармоническая в
– гармоническая в  функция, сопряженная
функция, сопряженная 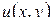 (см. § 1.5). Тогда функция
(см. § 1.5). Тогда функция 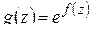 удовлетворяет в области
удовлетворяет в области  условиям теоремы 1.13 и, следовательно, ее модуль
условиям теоремы 1.13 и, следовательно, ее модуль 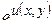 достигает наибольшего значения на границе
достигает наибольшего значения на границе  ; отсюда вытекает, что
; отсюда вытекает, что 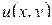 достигает наибольшего значения на границе
достигает наибольшего значения на границе 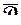 . Вводя вместо
. Вводя вместо 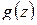 функцию
функцию 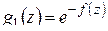 , убедимся, что наименьшее значение
, убедимся, что наименьшее значение 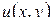 также достигается на границе
также достигается на границе 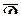 .
.
Теорема 1.14 геометрически означает, что график гармонической функции 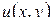 есть поверхность (рельеф) без вершин и впадин.
есть поверхность (рельеф) без вершин и впадин.

| 
|
Рис. 1.18. Рис. 1.19.
Задание для самостоятельной работы.
1) Доказать: если функция 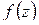 удовлетворяет в области
удовлетворяет в области  условиям теоремы 1.14 и не имеет нулей в
условиям теоремы 1.14 и не имеет нулей в  , то ее модуль достигает наименьшего значения на границе
, то ее модуль достигает наименьшего значения на границе  .
.
2) Найти графики (рельефы) гармонических функций:
а) 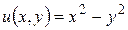 ; б)
; б) 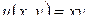 ; в)
; в) 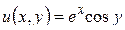 .
.
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
В приложениях операционного исчисления систематически используются следующие правила 10–70. Далее в 20–70 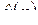 – L-изображение оригинала
– L-изображение оригинала 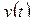 .
.
10 . Теорема линейности:
 ;
; 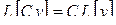
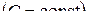 .
.
20. Теорема подобия:
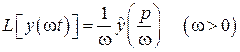 .
.
30. Теорема смещения:
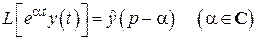 .
.
40. Теорема запаздывания:
 .
.
50. Изображение производных:
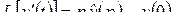 ,
,
 ,
,
. . .
 .
.
60. Изображение интеграла:
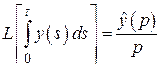 .
.
70.
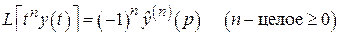 .
.
Свойство 10 непосредственно следует из определения (2.1). Предлагаем читателю доказать свойства 20–50. Отметим, что при доказательстве теоремы запаздывания существенно используется требование 20 в определении оригинала.
Замечание. В приложениях операционного исчисления к теории автоматического управления, радиотехнике, электротехнике оригинал 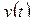 (выходной сигнал линейной стационарной цепи), как правило, удовлетворяет требованию
(выходной сигнал линейной стационарной цепи), как правило, удовлетворяет требованию 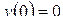 . В этом случае первая формула 50 принимает вид
. В этом случае первая формула 50 принимает вид
 .
.
Это означает: основная операция математического анализа – дифференцирование – в переводе на язык L-изображений 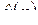 есть операция умножения на независимую переменную p. Аналогично формула 60 означает: другая основная операция математического анализа – интегрирование – в переводе на язык
есть операция умножения на независимую переменную p. Аналогично формула 60 означает: другая основная операция математического анализа – интегрирование – в переводе на язык
L-изображений есть операция деления на независимую переменную p. Эти два факта позволяют в ряде случаев заменить задачи, требующие применение методов математического анализа, равносильными более простыми задачами алгебры. В этом состоит основной замысел операционного исчисления.
Рассмотрим несколько примеров на применение формул 10 – 70.
Примеры. Найти L-изображения следующих функций.
1) 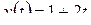 .
.
Решение. По формулам 10, 70 с учетом (2.2) имеем
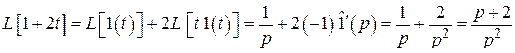 .
.
2) 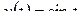 .
.
Решение. По формуле Эйлера (1.3) и формулам 10, (2.3) получим
 .
.
3) 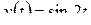 .
.
Решение. Обозначим 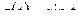 , тогда
, тогда 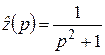 (пример 2). По формуле 20 найдем
(пример 2). По формуле 20 найдем
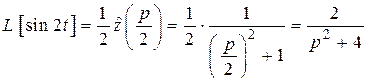 .
.
4) 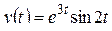 .
.
Решение. Обозначим  , тогда
, тогда 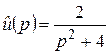 (пример 3). По формуле 30
(пример 3). По формуле 30
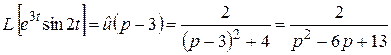 .
.
5) 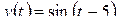 .
.
Решение. Имеем:
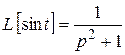 ;
; 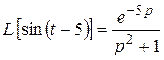 .
.
6) 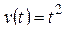 .
.
Решение. Аналогично примеру 1:
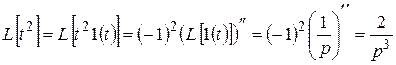 .
.
7) 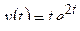 .
.
Решение. По формулам 70 и (2.2):
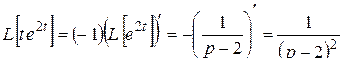 .
.
8) 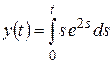 .
.
Решение. По формуле 60
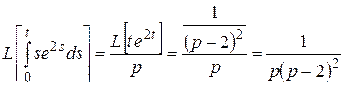
(учтен результат примера 7).
Задание для самостоятельной работы.
Пользуясь свойствами преобразования Лапласа найти L-изображения следующих функций:
а) 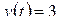 ; б)
; б) 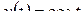 ; в)
; в) 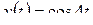 ; г)
; г) 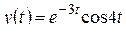 ;
;
д)  ; е)
; е) 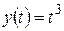 ; ж)
; ж) 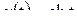 ; з)
; з) 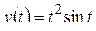 ;
;
и) 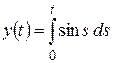 ; к)
; к) 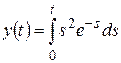 .
.
§ 2.3. ТАБЛИЦА НЕКОТОРЫХ L -ИЗОБРАЖЕНИЙ
Далее при вычислении L-изображений будут использоваться приводимые ниже формулы 1 – 14; первые две доказаны выше, остальные доказываются с помощью приемов, примененных при решении примеров в § 2.2.
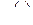
| 
|
| 
| 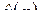
| ||
| 1. | 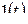
| 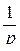
| 8. | 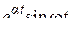
| 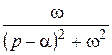
| |
| 2. | 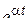
| 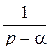
| 9. | 
| 
| |
| 3. | 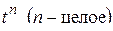
| 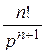
| 10. | 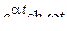
| 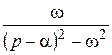
| |
| 4. | 
| 
| 11. | 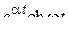
| 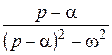
| |
| 5. | 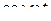
| 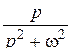
| 12. | 
| 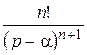
| |
| 6. | 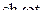
| 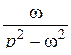
|
| 13. | 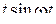
| 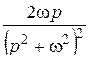
|
| 7. | 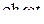
| 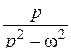
| 14. | 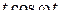
| 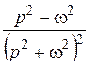
|
Подробные таблицы L-изображений содержатся в книге [7].
Примеры. Пользуясь свойствами преобразования Лапласа и таблицей
L-изображений, найти L-изображения следующих функций.
1)  .
.
Решение. Представим произведение 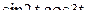 в виде разности синусов:
в виде разности синусов: 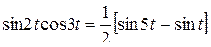 . Пользуясь теоремой линейности и затем формулой 8 из таблицы, получим:
. Пользуясь теоремой линейности и затем формулой 8 из таблицы, получим:

2) 
 .
.
Решение. Имеем:  , поэтому
, поэтому 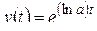 . По формуле 2 из таблицы найдем:
. По формуле 2 из таблицы найдем:
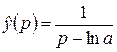 .
.
3) 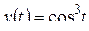 .
.
Решение. Представляя 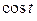 формулой Эйлера, получим:
формулой Эйлера, получим:
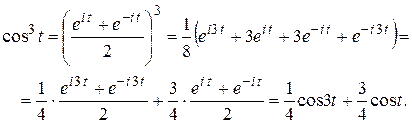
По теореме линейности и формуле 5 из таблицы найдем:
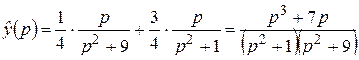 .
.
Задание для самостоятельной работы.
Найти L-изображения следующих функций:
а) 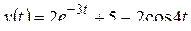 ; б)
; б) 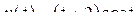 ; в)
; в) 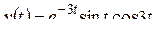 ;
;
г) 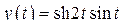 ; д)
; д) 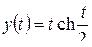 ; е)
; е) 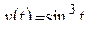 .
.
§ 2.4. ВОССТАНОВЛЕНИЕ ОРИГИНАЛА ПО ЕГО L -ИЗОБРАЖЕНИЮ
Одно из замечательных свойств преобразования Лапласа, широко используемое в приложениях операционного исчисления, состоит в том, что по
L -изображению 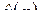 может быть восстановлен оригинал
может быть восстановлен оригинал 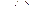 . Имеется общая формула, решающая эту задачу, называемая обратным преобразованием Лапласа (см. книгу [7]) . Эта формула неудобна для практического применения, поэтому мы ее здесь не приводим. Для многих приложений достаточно приводимое ниже частное правило, основанное на теории вычетов для аналитических функций комплексного переменного (§ 1.14).
. Имеется общая формула, решающая эту задачу, называемая обратным преобразованием Лапласа (см. книгу [7]) . Эта формула неудобна для практического применения, поэтому мы ее здесь не приводим. Для многих приложений достаточно приводимое ниже частное правило, основанное на теории вычетов для аналитических функций комплексного переменного (§ 1.14).
Напомним, что рациональная дробь (отношение двух многочленов)
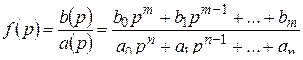
называется правильной, если степень числителя 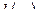 меньше степени знаменателя
меньше степени знаменателя 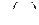 :
: 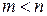 . В силу основной теоремы алгебры комплексных чисел имеет место разложение
. В силу основной теоремы алгебры комплексных чисел имеет место разложение
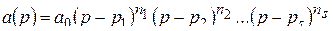 , (2.4)
, (2.4)
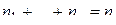 . Очевидно, числа
. Очевидно, числа  являются полюсами функции
являются полюсами функции  порядков соответственно
порядков соответственно  .
.
Теорема 2.1. Пусть L -изображение 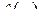 оригинала
оригинала 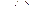 – правильная рациональная дробь со знаменателем (2.4). Тогда оригинал
– правильная рациональная дробь со знаменателем (2.4). Тогда оригинал 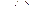 равен сумме вычетов функции
равен сумме вычетов функции 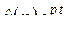 относительно полюсов
относительно полюсов 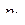 :
:
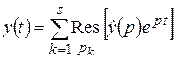 .
.
Эта формула называется формулой обращения. С учетом формулы (1.65) для вычета аналитической функции относительно полюса формула обращения принимает вид
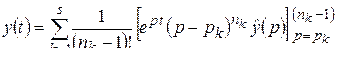 . (2.5)
. (2.5)
Следует помнить, что здесь производная порядка 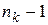 вычисляется (после сокращения в квадратных скобках на
вычисляется (после сокращения в квадратных скобках на 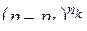 ) по комплексному переменному p при фиксированном t. В частном случае, когда
) по комплексному переменному p при фиксированном t. В частном случае, когда 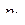 – полюс первого порядка,
– полюс первого порядка,  ; под производной порядка 0 понимается сама функция.
; под производной порядка 0 понимается сама функция.
Примеры. Найти оригиналы по данным L-изображениям.
1) 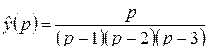 .
.
Решение. Здесь 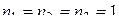 . По формуле обращения (2.5)
. По формуле обращения (2.5)
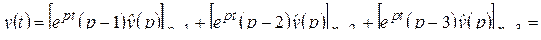


2) 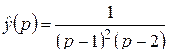 .
.
Решение. По формуле (2.5)
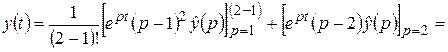
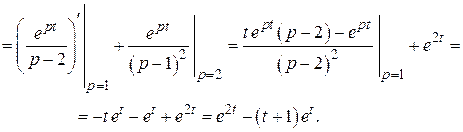
3)  .
.
Решение. По формуле (2.5)

Замечание. Для вычисления оригиналов может быть использовано правило разложения правильной рациональной дроби в сумму простейших дробей. В рассмотренном выше примере 1 разложение имеет вид
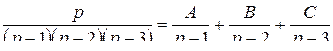 .
.
Вычисления методом неопределенных коэффициентов дают: 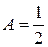 ,
,  ,
, 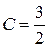 . Применяя к слагаемым формулу 2 из таблицы изображений и затем теорему линейности (справа налево), получим результат
. Применяя к слагаемым формулу 2 из таблицы изображений и затем теорему линейности (справа налево), получим результат
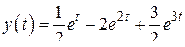 ,
,
совпадающий с полученным выше по формуле обращения. В примере 2 разложение имеет (после вычислений) вид
 .
.
Применение теоремы линейности и формул 2, 12 из таблицы изображений дает формулу для 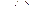 , полученную выше по формуле обращения (проверьте это).
, полученную выше по формуле обращения (проверьте это).
Задание для самостоятельной работы.
Восстановить оригиналы по данным L-изображениям:
а)  ; б)
; б) 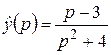 ; в)
; в) 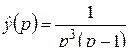 ;
;
г) 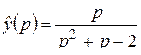 ; д)
; д) 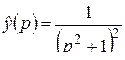 ; е)
; е) 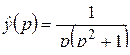 .
.
ФОРМУЛА ДЮАМЕЛЯ
В § 2.7 было установлено удобное правило описания линейных стационарных цепей на языке L-изображений с помощью передаточной функции – формулы (2.11), (2.12). Укажем часто применяемый способ описания цепей этого класса на языке оригиналов с использованием понятия «свертка». Для большей наглядности и для упрощения записей рассмотрим частный случай цепи (2.10):
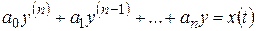 . (2.20)
. (2.20)
Выходной сигнал 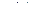 вычисляется по входному сигналу
вычисляется по входному сигналу 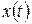 как решение задачи Коши для дифференциального уравнения (2.20) при нулевых начальных условиях:
как решение задачи Коши для дифференциального уравнения (2.20) при нулевых начальных условиях:
 .
.
Полученное далее правило остается верным для цепей общего вида (2.10).
|
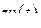 реакцию цепи (2.20) на сигнал
реакцию цепи (2.20) на сигнал 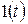 (рис. 2.12). Это означает, что
(рис. 2.12). Это означает, что 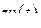 – решение задачи Коши
– решение задачи Коши

|
(2.21)
Теорема 2.3. Реакция 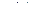 линейной стационарной цепи (2.20) на входное воздействие
линейной стационарной цепи (2.20) на входное воздействие 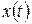 дается формулой
дается формулой
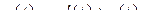 , (2.22)
, (2.22)
где 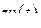 – функция (2.21).
– функция (2.21).
Доказательство. Достаточно проверить справедливость для функции (2.22) равенства  , где
, где 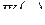 – передаточная функция цепи (2.20). Из определения функции
– передаточная функция цепи (2.20). Из определения функции 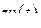 следует:
следует:
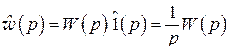 .
.
Применяя к обеим частям равенства (2.22) операцию L, с учетом теоремы о свертке (2.19), формулы для L-изображения производной и требования 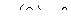 получим:
получим:
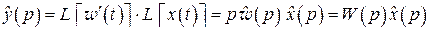 .
.
Теорема доказана.
Формула (2.22) называется формулой Дюамеля. Функция 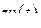 называется переходной функцией линейной стационарной цепи (2.20).
называется переходной функцией линейной стационарной цепи (2.20).
Пример. Найти переходную функцию линейной стационарной цепи
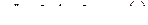 .
.
Пользуясь формулой Дюамеля, найти реакцию цепи на гармонику  .
.
Решение. Переходная функция 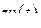 есть решение задачи Коши вида (2.21):
есть решение задачи Коши вида (2.21):
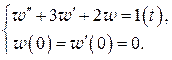
Применяя к обеим частям уравнения операцию L, вычисляя затем с учетом формулы  L-изображение
L-изображение 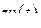 и разлагая полученную рациональную дробь в сумму элементарных дробей, получим
и разлагая полученную рациональную дробь в сумму элементарных дробей, получим
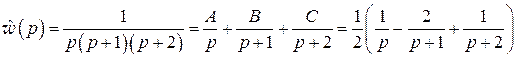 ,
,
откуда по правилу восстановления оригинала по L-изображению
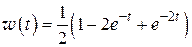 .
.
В силу теоремы 2.3 для вычисления реакции цепи на входной сигнал  нужно «свернуть» его с производной
нужно «свернуть» его с производной 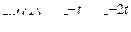 по формулам (2.22), (2.18):
по формулам (2.22), (2.18):
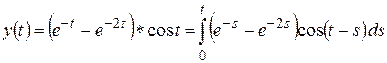 .
.
Вычисление этого интеграла с использованием приема «возвратного» интегрирования дает искомый результат:
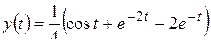 .
.
Задание для самостоятельной работы.
Найти переходные функции линейных стационарных цепей:
а) 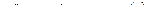 ; б)
; б) 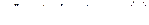 ; в)
; в)  .
.
Пользуясь формулой Дюамеля, найти реакции этих цепей на сигналы  ,
, 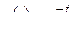 .
.
§ 2.10. ДЕЛЬТА-ФУНКЦИЯ.
ФИЛЬТРУЮЩЕЕ СВОЙСТВО ДЕЛЬТА-ФУНКЦИИ
В заключение изложим кратко широко применяемый в расчетах прием, предложенный в начале прошлого века английским физиком Дираком.
Определение 2.7. Дельта-функцией называется производная функции Хевисайда:
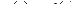 . (2.23)
. (2.23)
Из определения следует:
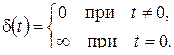
(при 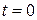 «касательная» к графику функции
«касательная» к графику функции 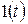 – см. рис. 2.3 – направлена вертикально, поэтому ее угловой коэффициент
– см. рис. 2.3 – направлена вертикально, поэтому ее угловой коэффициент 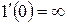 ). Очевидно,
). Очевидно, 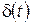 не является функцией в обычном смысле; в современной терминологии является обобщенной функцией или распределением (см. книгу [14]). В основе приложений дельта-функции лежит правило, называемое ее фильтрующим свойством. Мы приведем это правило с кратким пояснением и укажем приложение к теории автоматического управления.
не является функцией в обычном смысле; в современной терминологии является обобщенной функцией или распределением (см. книгу [14]). В основе приложений дельта-функции лежит правило, называемое ее фильтрующим свойством. Мы приведем это правило с кратким пояснением и укажем приложение к теории автоматического управления.

|
Из (2.23) следует (см. рис. 2.13): при любом 
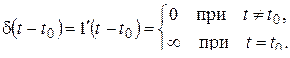 (2.24)
(2.24)
Точка  называется носителем функции
называется носителем функции  .
.
Теорема 2.4. Для любой непрерывной на оси функции  и любой
и любой  верно равенство
верно равенство
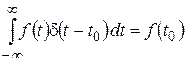 . (2.25)
. (2.25)
Таким образом, дельта-функция с носителем  «отбирает» из всех значений функции значение в точке
«отбирает» из всех значений функции значение в точке  – фильтрует множество значений.
– фильтрует множество значений.
Приведем нестрогое пояснение. Формальные вычисления по формуле (2.24) дают:
при 
 ,
,
при 
 .
.
Поэтому
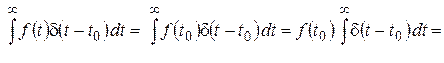
 .
.
Следствие. L-изображение функции 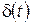 равно 1:
равно 1:
 . (2.26)
. (2.26)
В самом деле, из определения (2.1) преобразования Лапласа с учетом 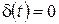 при
при 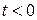 и фильтрующего свойства (2.25) получаем:
и фильтрующего свойства (2.25) получаем:
 .
.

|
Рассмотрим линейную стационарную цепь с передаточной функцией 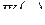 . Обозначим
. Обозначим  реакцию цепи на входной сигнал
реакцию цепи на входной сигнал 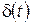 (рис. 2.14). Функция
(рис. 2.14). Функция  называется весовой функцией линейной стационарной цепи.
называется весовой функцией линейной стационарной цепи.
Лемма 2.4. Передаточная и весовая функции линейной стационарной цепи связаны соотношением
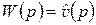 . (2.27)
. (2.27)
Доказательство. По формулам (2.11), (2.26) имеем:
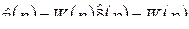 .
.
Теорема 2.5. Реакция  линейной стационарной цепи (2.10) с весовой функцией
линейной стационарной цепи (2.10) с весовой функцией  на входное воздействие
на входное воздействие 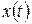 дается формулой
дается формулой
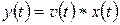 . (2.28)
. (2.28)
Доказательство. По формулам (2.19), (2.27) получаем:
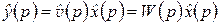 ,
,
откуда следует требуемое.
Пример. Решить пример из § 2.9, пользуясь понятием весовой функции и теоремой 2.5.
Решение. Весовая функция  есть решение задачи Коши
есть решение задачи Коши
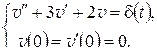
Применяя к обеим частям уравнения операцию L и используя формулу (2.26) для L-изображения дельта-функции:  , после простых вычислений
, после простых вычислений
найдем:
 ,
,
откуда
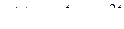 .
.
По формуле (2.28) получаем, как и в § 2.9:
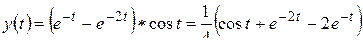 .
.
Задание для самостоятельной работы.
Решить примеры а), б), в), указанные в конце § 2.9, пользуясь понятием весовой функции и теоремой 2.5.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Маркушевич А.И. Введение в теорию аналитических функций /
А.И. Маркушевич, Л.А. Маркушевич. – М.: Просвещение, 1977.
2. Шабат Б.В. Введение в комплексный анализ / Б.В. Шабат. – М.: Наука, 1976. – Ч. 1.
3. Поддубный Г.В. Математический анализ для радиоинженеров /
Г.В. Поддубный, Р.К. Романовский. – М.: Воениздат, 1976.
4. Краснов М.Л. Функции комплексного переменного. Операционное исчисление. Теория устойчивости / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. – М.: Наука, 1971.
5. Мышкис А. Д. математика для втузов (специальные курсы) /
А.Д. Мышкис. – М.: Наука, 1971.
6. Лебедев Н.Н. Специальные функции и их приложения / Н.Н. Лебедев. – М.: ГИТТЛ, 1953.
7. Диткин В.А. Введение в комплексный анализ / В.А. Диткин,
А.П. Прудников. – М.: ГИФМЛ, 1961.
8. Мартыненко В.С. Операционное исчисление / В.С. Мартыненко. – Киев: Высшая школа, 1973.
9. Ройтенберг Я.Н. Автоматическое управление / Я.Н. Ройтенберг. – М.: Наука, 1978.
10. Попов Е.П. Теория линейных систем автоматического регулирования и управления / Е.П. Попов. – М.: Наука, 1978.
11. Чаки Ф. Современная теория управления / Ф. Чаки. – М.: Мир, 1975.
12. Шаталов А.С. Теория автоматического управления / А.С. Шаталов. – М.: Энергия, 1977.
13. Воронов А.А. Устойчивость, управляемость, наблюдаемость /
А.А. Воронов. – М.: Наука, 1978.
14. Владимиров В.С. Уравнения математической физики / В.С. Владимиров, В.В. Жаринов. – М.: ФМЛ, 2000.
Министерство образования и науки Российской Федерации

Государственное образовательное учреждение
высшего профессионального образования
«Омский государственный технический университет»

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Учебное пособие
Омск
Издательство ОмГТУ
2010
[1] Такие отображения будут более подробно рассмотрены в § 1.18.
[2] Доказательство утверждения в) требует привлечения математического аппарата, выходящего за рамки пособия.
[3] Существование и непрерывность производных второго порядка функций 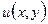 ,
, 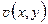 следует из того, что аналитическая функция имеет производные всех порядков (см. § 1.8).
следует из того, что аналитическая функция имеет производные всех порядков (см. § 1.8).
[4] Здесь и далее предполагается, что дуга, вдоль которой берется интеграл, без самопересечения и является гладкой или кусочно-гладкой. Гладкость означает, что в каждой точке дуги можно провести касательную, при этом направление касательной меняется непрерывно при движении точки по кривой. Если непрерывная дуга состоит из конечного числа гладких дуг, то она называется кусочно-гладкой.
[5] Существование интеграла обеспечено, если подынтегральная функция непрерывна на кусочно-гладкой дуге AB; см. замечание к свойству 6°.
[6] В дальнейшем, если не указано направление обхода контура интегрирования, то будем считать, что обход совершается против часовой стрелки.
[7] При доказательстве этого утверждения в векторном анализе предполагалась непрерывность частных производных от координат вектора, означающая в нашем случае непрерывность частных производных от 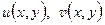 , т. е. непрерывность
, т. е. непрерывность 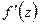 . Таким образом, проводимое доказательство является строгим при дополнительном предположении о непрерывности производной
. Таким образом, проводимое доказательство является строгим при дополнительном предположении о непрерывности производной 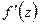 в области D1 . Можно доказать теорему Коши и без этого предположения, однако доказательство значительно усложнится.
в области D1 . Можно доказать теорему Коши и без этого предположения, однако доказательство значительно усложнится.
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ................................................................................................. 4
Раздел 1. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО................................................................................ 6
§ 1.1. Комплексные числа................................................................... 6
§ 1.2. Функции комплексного переменного....................................... 8
§ 1.3. Структура точечных множеств на плоскости........................ 10
§ 1.4. Производная функции комплексного переменного.............. 11
§ 1.5. Аналитические функции. Комплексный потенциал............... 15
§ 1.6. Интеграл от функции комплексного переменного................ 19
§ 1.7. Теорема Коши......................................................................... 23
§ 1.8. Интегральная формула Коши................................................ 27
§ 1.9. Степенные ряды...................................................................... 30
§ 1.10. Некоторые элементарные функции...................................... 34
§ 1.11. Ряд Тейлора.......................................................................... 37
§ 1.12. Ряд Лорана............................................................................ 41
§ 1.13. Изолированные особые точки аналитической функции..... 44
§ 1.14. Вычеты.................................................................................. 46
§ 1.15. Применение вычетов к вычислению несобственных
интегралов............................................................................. 49
§ 1.16. Принцип аргумента.............................................................. 53
§ 1.17. Принцип максимума............................................................. 55
§ 1.18. Понятие о комформном отображении................................. 58
Раздел 2. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ................................................ 67
§ 2.1. Оригинал. L-изображение оригинала.................................... 67
§ 2.2. Свойства преобразования Лапласа........................................ 70
§ 2.3. Таблица некоторых L-изображений...................................... 73
§ 2.4. Восстановление оригинала по его L-изображению............... 74
§ 2.5. Применение операционного исчисления к решению
дифференциальных уравнений............................................... 76
§ 2.6. Применение операционного исчисления
к решению систем дифференциальных уравнений................ 78
§ 2.7. Передаточная функция линейной стационарной цепи.......... 80
§ 2.8. Свертка двух функций. Теорема о свертке............................ 84
§ 2.9. Формула Дюамеля.................................................................. 85
§ 2.10. Дельта-функция. Фильтрующее свойство дельта-функции. 87
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.............................................................. 90
ПРЕДИСЛОВИЕ
Основное назначение данного учебного пособия – методическое обеспечение читаемых студентам всех технических специальностей курсов «Теория автоматического управления», «Математический анализ и теория функций комплексного переменного (ТФКП)». В соответствии с этим пособие состоит из двух разделов: «Элементы ТФКП» и «Операционное исчисление» (такой порядок изложения обусловлен тем, что построение операционного исчисления опирается на методы ТФКП). Содержание разделов соответствует требованиям госстандартов по указанным дисциплинам.
При изложении элементов ТФКП с самого начала внимание читателей обращено на то, что объектом изучения в этой теории является узкий класс функций: аналитические функции комплексного переменного; многочисленные приложения ТФКП к математике и физике связаны с замечательными свойствами этого класса функций. Изложены с подробным обоснованием элементарные основы теории аналитических функций: интегральная теорема и интегральная формула Коши, разложения в ряды Тейлора и Лорана, теорема о вычетах. В качестве приложения вычетов приведено и проиллюстрировано на примерах правило вычисления спектральной плотности сигналов (лемма Жордана). Заключительные параграфы раздела знакомят читателя с базовыми принципами комплексного анализа: принципом аргумента и принципом максимума, лежащими в основе многих приложений ТФКП, и с элементами теории конформных отображений, играющей важную роль в теории краевых задач математической физики.
Изложение раздела «Операционное исчисление» подразделяется на три части (этапа). В первой части (§ 2.1–2.4) излагаются и иллюстрируются на ряде примеров основные понятия и правила операционного исчисления, в том числе удобное правило восстановления оригинала по его лапласовому изображению с помощью вычетов (формула обращения).
Во второй части (§ 2.5, 2.6) этот аппарат применяется к решению задачи Коши для линейных дифференциальных уравнений и систем линейных дифференциальных уравнений с постоянными коэффициентами. Предложен способ решения задачи Коши для линейной системы приведением к стандартному
виду
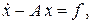
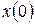 задано
задано
и последующим применением преобразования Лапласа; здесь в построении решения участвует резольвента 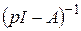 матрицы А системы.
матрицы А системы.
Третья часть (§ 2.7–2.10) посвящена приложению к теории автоматического управления. Вначале вводятся и иллюстрируются на примерах фундаментальные понятия «линейная стационарная цепь (ЛСЦ)», «передаточная функция ЛСЦ», указана связь между передаточной функцией и другим фундаментальным понятием теории ЛСЦ – частотной характеристикой. Затем после проведенной в § 2.8 подготовки (вводится понятие «свертка», доказывается теорема о свертке) выводится широко применяемая в инженерных расчетах формула Дюамеля, представляющая собой удобное правило задания ЛСЦ на языке оригиналов. Заключительный параграф кратко знакомит читателя с дельта-функцией и ее приложением к теории ЛСЦ.
В обоих разделах в конце каждого параграфа приводится задание для самостоятельной работы.
Помимо указанного выше основного назначения учебное пособие может быть использовано при чтении радиотехнических и электротехнических дисциплин, где применяются методы операционного исчисления и ТФКП.
Авторы
Раздел 1. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
КОМПЛЕКСНЫЕ ЧИСЛА
В этом параграфе мы напомним читателю простейшие сведения о комплексных числах, используемые в дальнейшем.
Пусть задана прямоугольная система координат на плоскости. Тогда каждое комплексное число 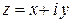 может быть изображено точкой плоскости с координатами
может быть изображено точкой плоскости с координатами 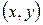 . В частности, действительные числа
. В частности, действительные числа 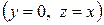 изображаются точками оси абсцисс, называемой поэтому действительной осью; чисто мнимые числа
изображаются точками оси абсцисс, называемой поэтому действительной осью; чисто мнимые числа 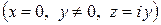 изображаются точками оси ординат, называемой поэтому мнимой осью.
изображаются точками оси ординат, называемой поэтому мнимой осью.
Полярные координаты 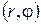 точки (рис. 1.1) называются соответственно модулем и аргументом комплексного числа
точки (рис. 1.1) называются соответственно модулем и аргументом комплексного числа  и обозначаются соответственно
и обозначаются соответственно  ,
, 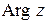 . Очевидно, при
. Очевидно, при 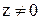
 имеет бесконечно много значений:
имеет бесконечно много значений: 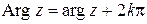
 , где
, где 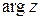 – какое-либо одно из значений
– какое-либо одно из значений 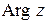 . Условимся в дальнейшем под
. Условимся в дальнейшем под 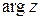 понимать значение
понимать значение 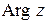 , заключенное в промежутке
, заключенное в промежутке 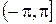 :
:
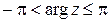 ,
,
и называть его главным значением аргумента  . При
. При  аргумент
аргумент  не определен.
не определен.
Из рис. 1.1 следует
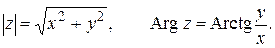
Так как 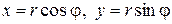 , то
, то
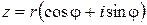 . (1.1)
. (1.1)
Это выражение называют тригонометрической формой комплексного числа  .
.
Пусть имеются два комплексных числа 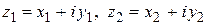 . Тогда
. Тогда
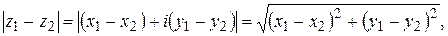
следовательно, модуль разности двух комплексных чисел равен расстоянию между точками, изображающими эти числа. По свойству сторон треугольника (см. рис. 1.2) получаем:
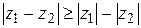 . (1.2)
. (1.2)
Далее имеем
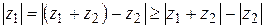 ,
,
откуда
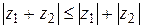 .
.
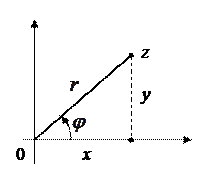
| 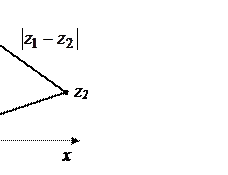
|
Рис. 1.1. Рис. 1.2.
Это неравенство легко распространяется на случай любого числа слагаемых:
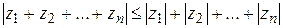 . (1.3)
. (1.3)
Пусть 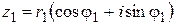 ,
, 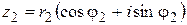 , тогда
, тогда

т. е. при умножении двух комплексных чисел их модули перемножаются, аргументы складываются (и, следовательно, при делении модули делятся, аргументы вычитаются). Отсюда сразу следует формула Муавра:
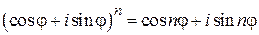 . (1.4)
. (1.4)
Формула (1.4) позволяет получить простое правило извлечения корня п-й степени из комплексного числа. Пусть 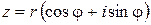 – заданное число,
– заданное число,  – корень п-й степени из
– корень п-й степени из  (т. е.
(т. е.  ). Тогда
). Тогда
 ,
,
откуда 
 (
(  – некоторое целое число). Следовательно, всякий корень п-й степени из
– некоторое целое число). Следовательно, всякий корень п-й степени из  представляется формулой
представляется формулой
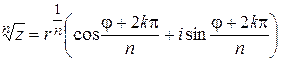 (1.5)
(1.5)
при некотором целом  . Подставляя в (1.5) последовательно
. Подставляя в (1.5) последовательно  , мы, очевидно, исчерпаем все возможные значения
, мы, очевидно, исчерпаем все возможные значения  .
.
Пусть 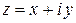 ; тогда комплексное число
; тогда комплексное число 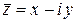 называется сопряженным к
называется сопряженным к  . Числа
. Числа  изображаются точками, симметричными относительно действительной оси. В частности, действительные числа (и только они) сопряжены себе. Легко проверяются равенства:
изображаются точками, симметричными относительно действительной оси. В частности, действительные числа (и только они) сопряжены себе. Легко проверяются равенства:
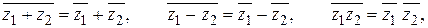
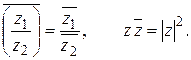
В дальнейшем действительную и мнимую части комплексного числа 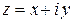 будем обозначать соответственно
будем обозначать соответственно 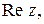
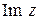 :
:
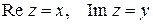 .
.
Очевидны равенства
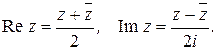
Задание для самостоятельной работы.
1) Найти модуль и аргумент комплексных чисел:
а) 1; б) –3; в) 2i; г)  ; д)
; д)  ; е)
; е)  .
.
2) Указать, где расположены точки z, для которых:
а) 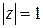 ; б)
; б) 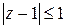 ; в)
; в)  ; г)
; г)  ;
;
д) 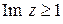 ; е)
; е) 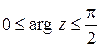 ; ж)
; ж) 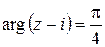 .
.
3) Вычислить:
а) 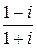 ; б)
; б) 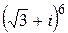 ; в)
; в) 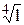 ; г)
; г) 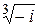 ; д)
; д) 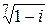 .
.
Дата: 2018-12-28, просмотров: 500.
