Цель работы: «Овладение методикой построения вариационного ряда и его графиков».
Задание 1.
Составить вариационный ряд по данным протокола наблюдений.
Вычислить относительные частоты. Результаты занести в таблицу:
| 
| 
| |
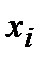
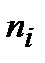
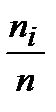
где n – объём выборки;
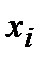– значения элементов выборки;
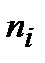– частота повторения i-го значения;
Wi = 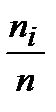– относительная частота.
Задание 2.
Построить графики вариационного ряда: (полигон частот и гистограмму относительных частот).
Задание 3.
Составить эмпирическую функцию распределения
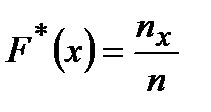
где n – объём выборки;
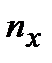– число вариант, меньших х.
Задание 4.
Построить график эмпирической функции распределения.
Вопросы:
1. Что такое генеральная и выборочная совокупности?
2. Как составить вариационный ряд?
3. Чему равен объём выборки?
4. Что такое относительная частота?
5. Статистическое распределение выборки.
6. Графики вариационного ряда.
7. Эмпирическая функция распределения и её свойства.
72
Вариант 1
| 4 | 6 | 0 | 2 | 1 | 3 | 3 | 1 | 2 | 5 | 3 | 1 2 | 2 | 4 | 4 | 4 | 3 | 2 | 5 |
| 2 | 5 | 1 | 2 | 3 | 0 | 3 | 0 | 5 | 1 | 2 | 1 3 | 0 | 4 | 0 | 2 | 2 | 1 | 0 |
| 5 | 1 | 4 | 2 | 4 | 2 | 1 | 3 | 1 | 0 | 6 | 1 2 | 1 | 4 | 2 | 2 | 0 | 2 | 4 |
2212 2
n = 65
начало первого интервала: 0 длина интервала: 1
Вариант 2
| 0 0 | 0 | 1 | 0 | 0 | 1 | 3 | 1 | 1 | 1 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 0 | 1 |
| 1 1 | 1 | 3 | 2 | 0 | 0 | 1 | 4 | 1 | 0 | 0 | 0 | 2 | 0 | 1 | 2 | 1 | 2 | 0 |
| 1 2 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 2 | 0 | 1 | 0 | 0 | 0 | 2 |
| 1 2 | 0 | 1 | 1 | 1 | 2 | 0 | 0 | 2 | 1 | 1 | 2 | 2 | 0 | 0 | 0 | 2 | 0 | 0 |
010 0
n = 84
начало первого интервала: 0 длина интервала: 1
Вариант 3
| 4 | 1 | 9 | 6 | 11 | 11 | 6 | 5 | 10 | 4 | 10 | 10 | 12 | 10 | 9 |
| 6 | 6 | 8 | 4 | 10 | 2 | 5 | 6 | 8 | 6 | 7 | 2 | 2 | 6 | 12 |
| 2 | 8 | 8 | 11 | 9 | 6 | 7 | 4 | 5 | 9 | 7 | 9 | 5 | 9 | 10 |
| 5 | 8 | 6 | 10 | 8 | 8 | 6 | 9 | 10 | 8 | 6 | 1 | 3 | 10 | 4 |
| 8 | 6 | 10 | 9 | 10 | 3 | 6 | 11 |
n = 68
начало первого интервала: 1 длина интервала: 1
Вариант 4
| 2 | 0 | 2 | 6 | 2 | 3 | 5 | 3 8 | 3 | 6 | 4 | 5 | 2 | 6 | 6 | 5 | 5 | 8 | 8 |
| 3 | 5 | 3 | 2 | 4 | 5 | 2 | 1 6 | 9 | 7 | 6 | 7 | 4 | 5 | 6 | 5 | 6 | 8 | 3 |
| 6 | 5 | 5 | 1 | 7 | 6 | 4 | 1 5 | 6 | 4 | 7 | 2 | 8 | 8 | 2 | 8 | 2 | 1 | 6 |
n = 60
начало первого интервала: 0 длина интервала: 1
Вариант 5
| 2 | 0 0 | 3 | 1 | 2 2 | 2 | 3 | 4 | 1 | 2 | 3 | 3 | 2 | 1 1 | 3 3 | 0 |
| 4 | 1 3 | 3 | 0 | 1 0 | 0 | 1 | 2 | 1 | 1 | 3 | 2 | 3 | 0 1 | 0 4 | 2 |
| 3 | 1 2 | 1 | 1 | 1 1 | 2 | 1 | 2 | 5 | 2 | 1 | 3 | 2 | 3 1 | 1 1 | 1 |
| 2 | 1 1 | 1 | 3 | 1 3 | 1 | 2 | 1 | 2 | 1 | 1 | 0 | 0 | 3 3 | 1 2 | 3 |
n = 80
начало первого интервала: 0 длина интервала: I
73
Вариант 6
7 1 1 555594 5385383
11 3 9683362744357
4 6529586 11774497
431664545578684 1
0 277596112779268
n = 80
начало первого интервала: 0 длина интервала: 1
Вариант 7
| 1 | 0 | 1 | 3 | 1 | 1 | 4 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 2 | 1 | 0 1 |
| 1 | 0 | 1 | 0 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | 1 | 2 | 1 | 1 | 1 | 2 | 3 | 0 1 |
| 0 | 2 | 2 | 0 | 2 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 1 | 2 | 0 1 |
| 2 | 1 | 1 | 0 | 1 | 2 | 0 | 2 | 2 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 3 | 1 | 2 2 |
| 2 | 0 | 2 | 0 | 2 | 1 | 0 | 3 | 1 | 1 | 3 |
n = 91
начало первого интервала:0 длина интервала: 1
Вариант 8
| 1 | 4 | 3 | 3 | 1 | 0 | 4 | 0 | 4 | 3 | 2 | 0 | 2 | 2 | 3 | 3 | 1 0 | 3 | 3 |
| 3 | 2 | 3 | 1 | 3 | 2 | 5 | 6 | 3 | 2 | 5 | 2 | 3 | 4 | 2 | 3 | 2 2 | 6 | 2 |
| 0 | 1 | 2 | 3 | 6 | 2 | 1 | 4 | 3 | 3 | 1 | 5 | 4 | 3 | 2 | 1 | 1 1 | 6 | 1 |
| 2 | 0 | 2 | 2 | 2 | 3 | |||||||||||||
n = 66
начало первого интервала:0 длина интервала: 1
74
Вариант 9
| 4 | 5 | 3 | 4 | 5 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 3 | 1 | 4 | 1 | 4 | 5 | 5 | 1 |
| 2 | 5 | 5 | 5 | 3 | 4 | 3 | 5 | 5 | 4 | 0 | 2 | 6 | 7 | 1 | 3 | 2 | 2 | 4 | 2 |
| 3 | 3 | 6 | 0 | 6 | 2 | 4 | 1 | 6 | 1 | 5 | 4 | 4 | 4 | 5 | 2 | 4 | 5 | 3 | 5 |
| 5 | 6 | 2 | 2 | 3 | 2 | 2 | 5 | 2 | 5 | 5 | 0 | 7 | 1 | 0 | 0 | 0 | 5 | 5 | 2 |
7 6 3 5 3
n = 85
начало первого интервала:0 длина интервала: 1
Вариант 10
| 7 | 8 | 4 | 0 | 4 | 6 | 5 | 4 | 3 | 2 | 4 | 8 | 6 | 2 | 2 |
| 5 | 3 | 6 | 6 | 5 | 5 | 3 | 5 | 6 | 7 | 8 | 9 | 5 | 2 | 5 |
| 4 | 5 | 6 | 6 | 3 | 6 | 5 | 4 | 5 | 10 | 3 | 7 | 5 | 3 | |
| 3 | 3 | 7 | 5 | 3 | 4 | 9 | 2 | 1 | 4 | 4 | 4 | 2 | 4 | 3 |
| 4 | 4 | 5 | 5 | 3 | 7 | 5 | 3 | 2 | 6 | 2 | 4 | 4 | 4 | 0 |
| 6 | 1 | 1 | 4 | 4 | 5 | 4 | 8 | 3 | 5 | 5 | 4 | 1 | 9 |
n=89
начало первого интервала: 0 длина интервала: 1
75
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы.
Основные источники:
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Юрайт, 2016.
2. Ш.А. Алимов и др. Алгебра и начала математического анализа 10-11 класс. – М.: Просвещение, 2016.
Дополнительные источники:
1. Колде Я.К. Практикум по теории вероятностей и математической статистике. – М.: Высшая школа, 1991.
2. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. – М.: Академия, 2003.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Юрайт, 2016.
4. Интернет-ресурсы:
mathprofi.ru
www.matburo.ru
www.lektorium.tv
Желаем успехов!
76
Дата: 2018-11-18, просмотров: 552.
