Цель работы: «Овладение методиками расчета математического ожидания и дисперсии ДСВ».
Задание 1.
Рассчитать математическое ожидание суммы и произведения двух дискретных случайных величин двумя
способами: составив общий закон распределения и по формуле математического ожидания
M(x) = р1х1 + р2х2 + р3х3 + … + рnхn
где х1, х2 , 
, хn – возможные значения дискретной величины;;
р1, р2, 
, рn – соответствующие вероятности этих значений.
Задание 2.
Найти дисперсию случайной величины Х – числа появлений события А в шести независимых испытаниях, если дано математическое ожидание М(х).
Указание: Написать биномиальный закон распределения вероятностей числа появлений события А в шести независимых испытаниях.
Биномиальное распределение вероятностей определяется формулой Бернулли:
Pn(k) =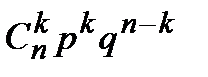 
где n – число испытаний;
k – частота появления события А.
р – вероятность появления события А в испытаниях.
q – вероятность непоявления события А.
Аданне 3.
Дискретная случайная величина Х имеет три возможных значения х1, х2 , х3 , причем х1 < х2 < х3 . Вероятности того, что Х примет значение х1, и х2 соответственно равны р1 и р2.
Найти закон распределения величины Х, зная ее математическое ожидание М(х) и дисперсию D(х).
D(x) =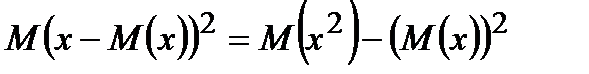 
62
Вопросы:
1. Что такое математическое ожидание случайной величины?
2. Свойства математического ожидания.
3. Как рассчитать математическое ожидание дискретной случайной величины?
4. Что такое дисперсия дискретной случайной величины?
5. Свойства дисперсии.
6. Формулы расчета дисперсии.
7. Дисперсия числа появлений события в независимых испытаниях.
Вариант 1
1.
| X | 0,1 | 0,23 | 0,37 | 0,5 |
| P | 0,1 | 0,2 | 0,6 | 0,1 |
| Y | 3 | 8 | 12 | 24,30 |
| G | 0,15 | 0,25 | 0,2 | 0,4 |
2. M(x) = 4,2
3.
X1 = 5
P1 = 0,7
P2 = 0,2
M(x) = 5,4
D(x) = 0,44
Вариант 2
1.
| X | 12,100 | 13,20 | 14,30 | 15,40 | 16,50 |
| P | 0,1 | 0,13 | 0,22 | 0,17 | 0,38 |
| Y | 0,8 | 1,400 | 2,200 | ||
| G | 0,3 | 0,3 | 0,4 |
2.
M(x) = 2,4
3.
X1 = 1
P1 = 0,1
P2 = 0,7
M(x) = 2,1
D(x) = 0,29
63
Вариант 3
1.
| X | 3,2 | 5,6 | 6,7 | 7,3 | 8,8 |
| P | 0,28 | 0,01 | 0,32 | 0,27 | 0,12 |
| Y | 0,15 | 0,17 | 0,19 | ||
| G | 0,7 | 0,1 | 0,2 |
2. M(x) = 1,8
3.
X1 = 2
P1 = 0,2
P2 = 0,2
M(x) = 3,4
D(x) = 0,64
Вариант 4
1.
| X | 0,28 | 0,73 | 1,2 | 1,7 |
| P | 0,7 | 0,08 | 0,2 | 0,02 |
| Y | 2,35 | 10,8 | 15,11 | 16 |
| G | 0,1 | 0,13 | 0,44 | 0,33 |
2. M(x) = 1,2
3. X1 = 3
P1 = 0,5
P2 = 0,4
M(x) = 3,6
D(x) = 0,44
Вариант 5
1.
| X | 28,8 | 29,3 | 37,5 | 43,8 |
| P | 0,13 | 0,13 | 0,13 | 0,61 |
| Y | 0,2 | 0,81 | 0,905 | 1,03 |
| G | 0,5 | 0,2 | 0,1 | 0,2 |
2. M(x) = 3,6
3.
X1 = 4
P1 = 0,4
P2 = 0,4
M(x) = 4,8
D(x) = 0,56
64
Вариант 6
1.
| X | 18,1 | 20,1 | 25,1 | ||
| P | 0,4 | 0,3 | 0,3 | ||
| Y | 0,12 | 0,38 | 1,57 | 3,13 | 4,2 |
| G | 0,15 | 0,18 | 0,17 | 0,27 | 0,23 |
2. M(x) = 4,8
3. X1 = 5
P1 = 0,6
P2 = 0,1
M(x) = 5,7
D(x) = 0,81
Вариант 7
1.
| X | 0,3 | 0,8 | 1,2 | 1,3 | 3,7 |
| P | 0,1 | 0,3 | 0,1 | 0,15 | 0,35 |
| Y | 41,8 | 42,2 | 45,3 | ||
| G | 0,4 | 0,3 | 0,3 |
2.
M(x) = 1,2
3.
X1 = 2
P1 = 0,6
P2 = 0,1
M(x) = 2,7
D(x) = 0,81
Вариант 8
1.
| X | 0,3 | 0,81 | 1,2 | 1,8 |
| P | 0,3 | 0,5 | 0,1 | 0,1 |
| Y | 31,3 | 42,5 | 51,6 | 58,2 |
| G | 0,14 | 0,28 | 0,31 | 0,27 |
2. M(x) = 1,8
3. X1 = 3
P1 = 0,4
P2 = 0,3
M(x) = 3,9
D(x) = 0,69
65
Вариант 9
1.
| X | 0,2 | 0,32 | 0,88 | ||
| P | 0,2 | 0,2 | 0,6 | ||
| Y | 3,7 | 15,8 | 16,1 | 25,8 | 31,2 |
| G | 0,21 | 0,22 | 0,2 | 0,2 | 0,17 |
2.
M(x) = 2,4
3.
X1 = 1
P1 = 0,3
P2 = 0,2
M(x) = 2,2
D(x) = 0,76
Вариант 10
1.
| X | 20,2 | 30,8 | 41,3 | ||
| P | 0,3 | 0,45 | 0,25 | ||
| Y | 1,2 | 3,7 | 7,28 | 9,15 | 10 |
| G | 0,28 | 0,12 | 0,15 | 0,27 | 0,18 |
2.
M(x) = 3,6
3.
X1 = 4
P1 = 0,6
P2 = 0,1
M(x) = 4,7
D(x) = 0,81
66
Контрольная работа.
1 вариант.
1. В страховом обществе застрахованы 1000 автомобилистов. Вероятность аварии в течение года р=0,2. Найти вероятность того, что число аварий больше 195 и меньше 210.
2. В студии 3 телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера.
3. Случайная величина Х принимает возможные значения 1 и 3, образующие полную группу. М(Х)=2,3. Найти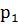 
; 
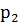и дисперсию D(Х).
4. Событие А наступает с вероятностью р=0,3. Проведено 5 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 2 раза; б) не меньше двух и не больше четырёх раз.
2 вариант.
1. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.
2. На стоянке 5 машин. Найти вероятность того, что среди этих машин:
а) две легковые; б) Не меньше двух и не больше четырех легковых машин.
3. Вероятность того, что событие А появится хотя бы один раз при двух независимых испытаниях равна 0,75. Найти вероятность появления события в одном испытании.
4. Случайная величина Х принимает три возможных значения: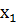 
=1; 
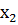=2;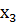 
=3. Математическое ожидание этой величины равно 2,3; математическое ожидание её квадрата рано 5,9. Найти вероятность ; ; 
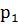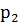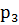
67
3 вариант.
1. Вероятность появления события в каждом из 300 независимых испытаний равна 0,8. Найти вероятность того, что событие появится не менее 245 раз.
2. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2-х деталей есть хотя бы одна стандартная.
3. Случайная величина Х принимает два возможных значения 1 и 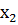, образующих полную группу. Вероятности их 0,2 и 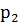. Математическое ожидание М(Х) равно 3,4. Найти 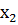; 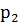и дисперсию случайной величины.
4. Событие А наступает с вероятностью р=0,4. Проведено 6 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 3 раза; б) не меньше трёх и не больше пяти раз.
4 вариант.
1. Монета брошена 200 раз. Найти вероятность того, что герб выпадет ровно 100 раз.
2. В коробке находится 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров.
Найти вероятность того, что среди них:
а) 3 белых шара;
б) меньше, чем 3 белых шара;
в) хотя бы 1 белый шар.
3. Случайная величина Х принимает два возможных значения 2 и 5,2, образующих полную группу. Известно математическое ожидание М(Х) равное 3,7. Найти вероятности 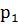; 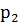и дисперсию случайной величины.
4. По каналу связи с одинаковыми вероятностями передаются 10 сигналов. Ввиду помех четыре из переданных сигналов при приеме искажаются. Найти вероятность того, что из двух наудачу взятых сигналов хотя бы один будет принят без искажений.
68
5 вариант.
1. Проведено 177 опытов. Вероятность появления положительного результата в каждом опыте равна р=0,9. Найти вероятность того, что не менее 150 и не более 160 опытов дадут положительный результат.
2. Событие А наступает с вероятностью р=0,35. Проведено 7 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 5 раз; б) не меньше трёх и не больше пяти раз.
3. Найти дисперсию случайной величины Х, заданной законом распределения:
| х | -5 | 2 | 3 | 4 |
| р | 0,4 | 0,3 | 0,1 | 0,2 |
4. Из 15 билетов выигрышными являются 4. Какова вероятность того, что среди двух билетов, взятых наудачу, есть хотя бы один выигрышный.
6 вариант.
1. Вероятность появления события в каждом из 100 независимых испытаний равна 0,8. Найти вероятность того, что событие появится не менее 75 раз.
2. Случайная величина Х принимает возможные значения: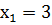 
; 
; 
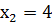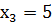. Математическое ожидание этой величины равно 4,1; математическое ожидание её квадрата равно 17,7. Найти вероятност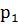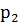и ; и .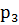
3. В группе спортсменов 6 человек. Вероятность присутствия среди них бегунов равна 0,25. Найти вероятность того, что среди этих спортсменов:
а) 3 бегуна; б) не меньше двух и не больше четырех бегунов.
4. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
69
7 вариант.
1. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
2. Событие А наступает с вероятностью 0,6. Проведено 4 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 3 раза; б) не меньше одного и не больше трёх раз.
3. Найти дисперсию случайной величины Х, заданной законом распределения:
| х | -2 | -1 | 1 | 2 |
| р | 0,5 | 0,4 | 0,3 | 0,2 |
4. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9364. Найти вероятность попадания в цель при одном выстреле.
8 вариант.
1. В страховом обществе застрахованы 1000 автомобилистов. Вероятность аварии в течение года р=0,3. Найти вероятность того, что число аварий больше 295 и меньше 310.
2. В студии 3 телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент равна 0,8. Найти вероятность того, что в данный момент включена хотя бы одна камера.
3. Случайная величина Х принимает возможные значения 1 и 5, образующие полную группу. М(Х)=4,3. Найти 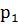; 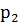и дисперсию D(Х).
4. Событие А наступает с вероятностью р=0,4. Проведено 5 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 3 раза; б) не меньше трех и не больше четырёх раз.
70
9 вариант.
1. Вероятность рождения девочки равна 0,49. Найти вероятность того, что среди 100 новорожденных окажется 50 девочек.
2. На стоянке 4 машины. Найти вероятность того, что среди этих машин:
а) две легковые; б) не меньше двух и не больше трех легковых машин.
3. Вероятность того, что событие А появится хотя бы один раз при трех независимых испытаниях равна 0,936. Найти вероятность появления события в каждом из испытаний при условии, что она постоянна.
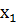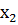4. Случайная величина Х принимает три возможных значения: =1; =2; 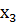=3. Математическое ожидание этой величины равно 1,9; математическое ожидание её квадрата рано 4,3. Найти вероятность ; ;
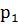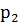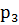
10 вариант.
1. Вероятность появления события в каждом из 200 независимых испытаний равна 0,8. Найти вероятность того, что событие появится не менее 155 раз.
2. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2-х деталей есть хотя бы одна стандартная.
3. Случайная величина Х принимает два возможных значения 1 и 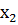, образующих полную группу. Вероятности их 0,2 и 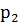. Математическое ожидание М(Х) равно 1,4. Найти 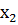; 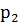и дисперсию случайной величины.
4. Событие А наступает с вероятностью р=0,3. Проведено 5 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно четыре раза; б) не меньше двух и не больше четырёх раз.
71
Практическая работа № 3.
Дата: 2018-11-18, просмотров: 453.
