Пусть из генеральной совокупности извлечена выборка.
При этом значение х1 наблюдалось n1 раз, значение х2 – n2 раз, значение хk – nk раз и 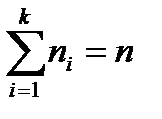 – объём выборки.
– объём выборки.
Наблюдаемые значения хi называются вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Число наблюдений называют частотами, а их отношения к объёму выборки 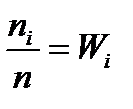 – относительными частотами.
– относительными частотами.
Определение. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
49
Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.
Пример. Задано распределение частот выборки объёма n = 20.
| хi | 2 | 6 | 12 |
| ni | 3 | 10 | 7 |
Написать распределение относительных частот.
Решение.
Найдём относительные частоты:
W1 = 3/20 = 0,15
W2 = 10/20 = 0,5
W3 = 7/20 = 0,35
Напишем распределение относительных частот:
| хi | 2 | 6 | 12 |
| Wi | 0,15 | 0,5 | 0,35 |
Контроль: 0,15 + 0,5 + 0,35 = 1
Обычно при эксперименте результаты наблюдений фиксируют в протоколе наблюдений в порядке их появления.
Например,
| 2 4 | 2 4 | 3 3 3 |
| 0 2 | 4 3 | 2 2 4 |
| 5 4 | 3 4 | 3 3 5 |
В выборке одно значение вариант может встречаться несколько раз, и поэтому целесообразно составлять таблицу или ряд вариант с частотами появления i-го значения.
Для составления варианта ряда нужно:
1. найти хmin и хmax значения выборки;
50
2. в первый столбец таблицы записать варианты значений случайной величины, начиная с хmin и до хmax;
3. просмотреть все элементы выборки в протоколе и отметить каждое значение во втором столбце таблицы;
4. подсчитать количество меток и записать соответствующее им число ni в третий столбец таблицы;
5. подсчитать количество элементов в выборке (объем выборки) n, которое должно быть равно:
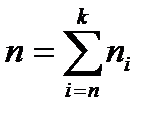
где k – количество наименований вариант в вариационном ряде.
Если объем выборки большой, то существуют способы подсчёта меток. Например, каждая пятая палочка перечёркивает четыре предыдущие:
| //// | //// | //// | /// |
| хi | ni | ni/n | |
| 0 | 1 | 1/21 | |
| 1 | 0 | 0 | |
| 2 | 5 | 5/21 | |
| 3 | //// // | 7 | 7/21 |
| 4 | //// | 6 | 6/21 |
| 5 | 2 | 2 | 2/21 |
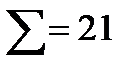
| 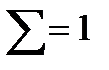
|
Если количество вариант k слишком велико или близко к объёму выборки, то целесообразно составить вариационный ряд по интервалам значений генеральной совокупности. Вариационный ряд по интервалам значений можно получить с помощью приведённого выше алгоритма, где во 2-м пункте следует заполнить первый столбец таблицы интервалами значений генеральной совокупности. Все интервалы выбираются одинаковой длины, т.е., чтобы хmin в последний интервал. Обычно начало интервала входит в интервал, а его конец – не входит.
Используют 2 вида графиков вариационных рядов: полигон и гистограмму.
51
Полигоном частот называют ломаную, отрезки которой соединяют точки
(х1; n1), (х2; n2). . .( хk; nk)
Полигоном относительных частот называют ломаную, отрезки которых соединяют точки (х1; w1), (х2; w2). . .( хk; wk)
Полигон относительных частот
wi
10/21
5/21
1 2 3 4 5 хi
ni /h
8
6
4
2
1 2 3 4 5
Гистограмма частот
Для построения полигона относительных частот на оси абсцисс откладывают варианты хi,, а на оси ординат – соответствующие им относительные частоты wi . Точки (хi ; wi) соединяют отрезками прямых и получают полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-й интервал.
52
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni /h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni /h. Площадь i-го частичного прямоугольника равна hni /h = ni – сумме частот вариант i-го интервала.
Дата: 2018-11-18, просмотров: 535.