Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Его можно задать таблично, аналитически (в виде формулы) и графически.

Например, таблица X x₁, x₂, x₃

                                 Р р₁, р₂, р₃

т.к. в одном испытании случайная величина принимает одно и только одно возможное значение, то события X = x₁, X = x₂ и т.д. организуют полную группу и, следовательно, 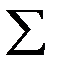вероятностей равны 1, т.е. р₁ + р₂ + р₃ + … + р_n = 1.

Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается 1 выигрыш в 500 рублей и 10 выигрышей по 100 рублей. Найти закон распределения случайной величины X – стоимости возможного выигрыша для 1 лотерейного билета.

Решение.

Возможные значения X: x₁ = 500; x₂ = 100; x₃ = 0.

Их вероятности: р₁ = 0,01; р₂ = 0,1; р₃ = 0,89.

 

X	500	100	0
Р	0,01	0,1	0,89

Контроль: 0,01 + 0,1 + 0,89 = 1.

 

 

3. Биномиальное распределение.

 

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р, и q = 1 – р.

 

33

Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях. Найдём закон распределения величины X. Для этого надо найти возможные значения случайной величины X и их вероятности.

Событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза …, либо n раз. Следовательно, x₁ = 0, x₂ = 1, x₃ = 2 …, x_n+1 = n. Вероятности этих возможных значений вычисляются по формуле Бернулли:

                                                                                                           (*)

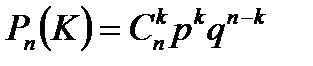где k = 1, 2, 3, …, n.

Формула (*) – аналитическое выражение искомого закона распределения. Биноми­наль­ным называется распределение вероятностей, определяемое формулой Бернулли.

 

Пример. Монета брошена 2 раза.

Написать в виде таблицы закон распределения случайной величины X – числа выпадений герба.

Решение.

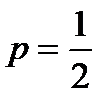 – вероятность появления герба в каждом испытании;  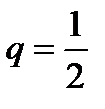– вероятность появления герба.

При двух бросаниях монеты герб может появиться 2 раза, 1 раз или совсем не появиться. Следовательно, возможные значения X: x₁ = 2, x₂ = 1, x₃ = 0.

Вероятности этих значений по формуле Бернулли:

 

 

 

.

 

 

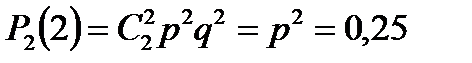
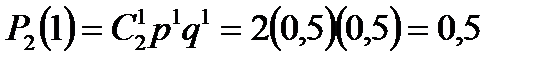
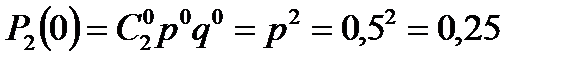Искомый закон распределения:

X	2	1	0
р	0,25	0,5	0,25

 

 

34

Многоугольник распределения:

  р_i

           0,5

          0,25

 х_i

1 2

 

Графическое представление биномиального закона распределения. ДСВ называется многоугольником распределения.

Распределение Пуассона.

Если число испытаний n велико, то пользуются формулой Лапласа. Однако, эта формула становится непригодной, если вероятность события мала 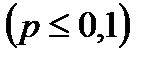. В этих случаях (n – велико, р – мало) при бегают к асимптотической формуле Пуассона.

Пусть нам надо найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз.

Сделаем допущение: произведение np сохраняет постоянное значение, а именно np = 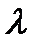. Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях n, остается неизвестным.

Воспользуемся формулой Бернулли:

.

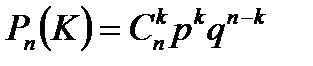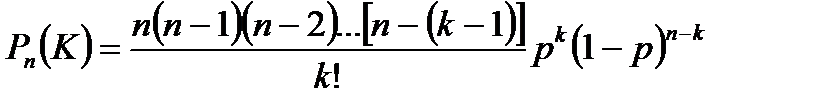
Т.к. np = 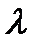, то p = 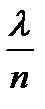, следовательно

 

 

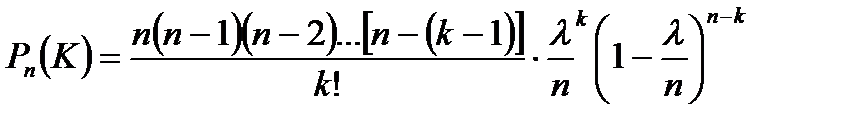
Т.к. n имеет очень большое значение, вместо Р_n(k) найдём 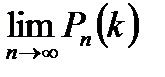. При этом мы найдём приближённое значение отыскиваемой вероятности, т.к. n хотя и велико, но конечно. Т.к. np = const, то при  , .

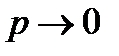35

Следовательно,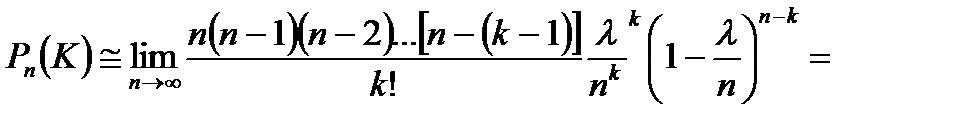

 

 

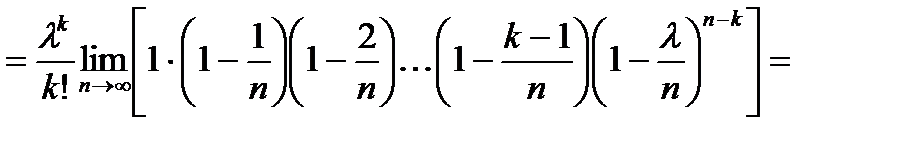
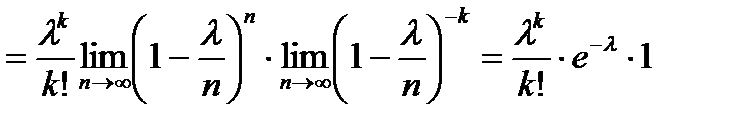
Т.о.

 

 

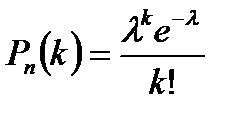
где е = 2,71828… – основание натурального ln.

– закон распределения Пуассона.

 

                             P_n(k)

 

 

                                                                   k

Пример. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделий повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделий.

Решение.

n = 5000

k = 3

p = 0,0002

.

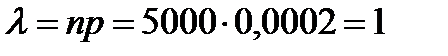По формуле Пуассона: Р₅₀₀₀(3) = 1³·е^-1/3! = 0,06

Ответ: 0,06

 

36

Примеры решения задач:

1. В магазине имеется 15 автомобилей определённой марки. Среди них 7 чёрного цвета, 6 серого и 2 белого. Представители фирмы обратились в магазин с предложением о продаже им 3 автомобилей этой марки, безразлично какого цвета. Составьте ряд распределения числа проданных автомобилей чёрного цвета при условии, что автомобили отбирались случайно.

Решение

Введём дискретную случайную величину Х = (число проданных автомобилей чёрного цвета). Х может принимать значения 0, 1, 2 и 3. Найдём соответствующие вероятности по классическому определению вероятности.

Всего способов выбрать 3 любых автомобиля из 15 будет:

.

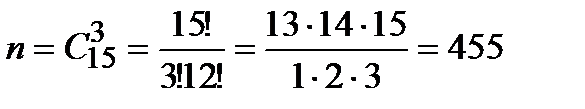Х = 0, если все автомобили не чёрные, таких было 8 штук, поэтому .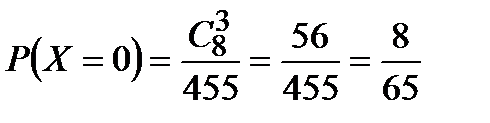

Х = 1, если один автомобиль чёрный, (выбираем из 7) и ещё два не чёрные (выбираем из 8 остальных), поэтому .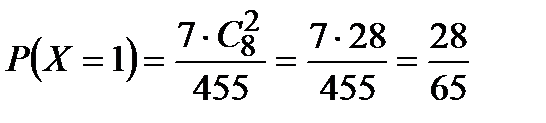

Х = 2, если два автомобиля чёрные, (выбираем из 7) и ещё один не чёрный (выбираем из 8 остальных), поэтому .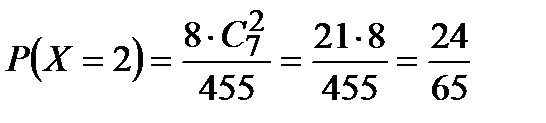

Х = 3, если все автомобили чёрные, вероятность .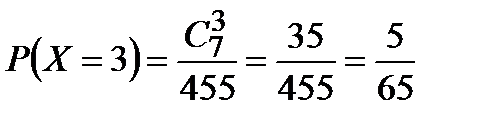

Ряд распределения случайной величины Х :

 

хi	0	1	2	3
рi	8/65	28/65	24/65	5/65

 

Сумма вероятностей равна 1, распределение найдено верно.

 

2. В городе 4 коммерческих банка. У каждого риск банкротства в течение года составляет 20%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года.

37

Решение

Пусть Х – дискретная случайная величина (ДСВ), равная числу банков, которые могут обанкротиться в течение следующего года. Она может принимать значения 0, 1, 2, 3, 4. ДСВ Х распределена по биноминальному закону с параметрами n=4, р=20%=0,2, поэтому найдём соответствующие вероятности по формуле Бернулли:

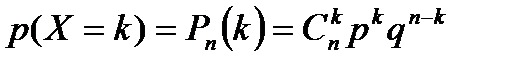 , где q = 1 – p  

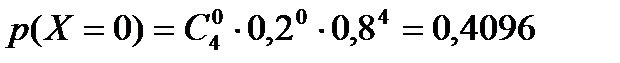
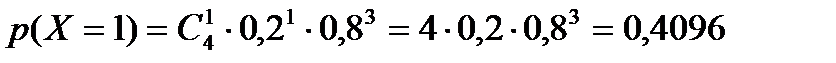
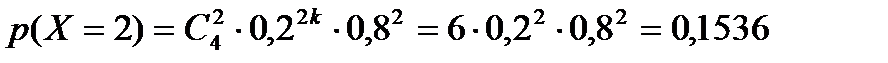
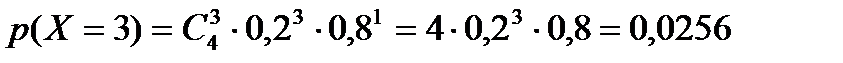
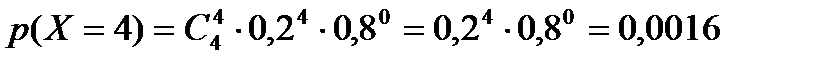
Таким образом, закон распределения случайной величины Х имеет вид:

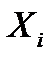
	0	1	2	3	4
	0,4096	0,4096	0,1536	0,0256	0,0016

0,4096+0,4096+0,1536+0,0256+0,0016=1

Следовательно, распределение найдено верно.

Вопросы для самопроверки:

1. Что такое случайная величина?

2. Определение дискретной случайной величины.

3. Что такое закон распределения дискретной случайной величины.

4. Что такое биноминальное распределение? В каком случае оно применяется? Формула.

5. В каких случаях применяют распределение Пуассона? Формула.