Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Как мы выяснили, закон распределения полностью характеризует случайную величину. Но иногда выгоднее пользоваться числами, которые описывают случайную величину суммарно. Такие числа называют числовыми характеристиками случайной величины.

1. Математическое ожидание дискретной случайной величины.

 

Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности.

38

Пусть случайная величина Х может принимать значения: x₁, x₂ , … x_n, верти которых соответственно равны р₁, р₂ , … р_n. Тогда математическое ожидание определяется равенством: М(х) = x₁ р₁ + x₂ р₂ + x_n р_n.

Если дискретная случайная величина Х принимает счётное множество возможных значений, то М(х) = 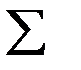x_i р_{i .}

Из определения следует, что математическое ожидание есть постоянная величина.

 

Пример. 1. Найти математическое ожидание случайной величины X, зная закон её распределения:

X	3	5	2
Р	0,1	0,6	0,3

М(х) = 3·0,1 + 5·0,6 + 2·0,3 = 3,9.

 

Пример. 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.

 

Решение.

Х – случайная величина числа появлений события А в одном испытании.

Х может принимать 2 значения: x₁ = 1, x₂ = 0

                                               р = р, р = q

М = 1·р + 0·q = p .

Вывод:

Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

 

 

Вероятностный смысл и свойства математического ожидания

 

Введём понятие относительной частоты. Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу произведённых испытаний

W(A) = m/n,

где m – число появлений события;

   n – общее число испытаний.

 

39

Очень похожие понятия, но отличие в том, что определение вероятности не требует, чтобы испытания производились в действительности; определение относительной частоты предполагает, что испытания были произведены.

Иначе можно сказать: вероятность вычисляют до опыта, относительную частоту – после опыта.

Пусть произведено n испытаний, в которых случайная величина X приняла m₁ раз значение х_k, причём:

m₁ + m₂ + … + m_k = n

Тогда сумма всех значений, принятых Х, равна:

x₁m₁ + x₂m₂ + … + x_km_k = n

 

Найдём среднее арифметическое 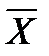всех значений, принятых случайной величиной:

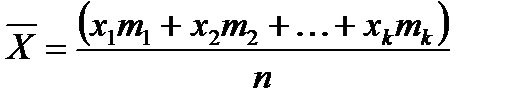
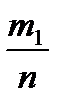 – относительная частота х₁ = W₁

 

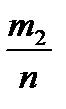 – относительная частота х₂ = W₂ и т.д.

тогда: .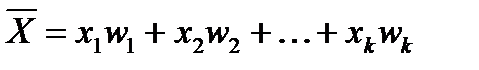

Допустим, что число испытаний достаточно велико. Тогда относительная частота приближённо равна вероятности появления события:

w₁ 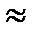p₁                        w₂ 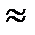p₂             … w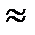_k p_k

Получаем: 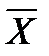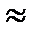x₁р₁ + x₂р₂ + … + x_kр_k

Правая часть равенства есть М(Х), т.е.

Математическое ожидание приближённо равно среднему арифметическому наблюдаемых значений случайной величины.

(При этом тем точнее, чем больше число испытаний).

Свойства.

 

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: М(С) = С.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

М(СХ) = СМ(Х).

40

Приведём 3 замечания:

 

1. Две случайные величины называют независимыми, если закон распре­деления одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае они зависимы.

 

2. Произведение независимых случайных величин Х и У определим как случай­ную величину ХУ, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение У. Вероятности возможных значений ХУ равны произведениям вероятностей возможных значений сомножителей.

 

3. Сумму случайных величин Х и У определим как случайную величину Х + У, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением У. Вероятности возможных значений Х + У равны произведениям вероятностей слагаемых.

 

 

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: М(ХУ) = М(Х)М(У).

 

Доказательство:

Пусть независимые случайные величины Х и У заданы своими законами распределения вероятностей:

Х	x1 x2		У	у1 у2
р	р1 р2		G	g1 g2

 

Составим все значения, которые может принимать случайная величина ХУ. Для этого перемножим все возможные значения Х на каждое возможное значение У. Учитывая замечание 2, получим:

 

ХУ	x1 у1	x2 у1	x1 у2	x2 у2
р	р1 g1	р2 g1	р1 g2	р2 g2

 

Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:

 

41

М(ХУ) = x₁ у₁· р₁ g₁ + x₂ у₁· р₂ g₁ + x₁ у₂· р₁ g₂ + x₂ у₂· р₂ g₂

или

М(ХУ) = у₁g₁(x₁р₁ + x₂ р₂) + у₂g₂ (x₁р₁ + x₂ р₂) = М(Х)М(У).

 

Следствие : Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их матема­тических ожиданий.

М( XYZ ) = M(X)M(Y)M(Z).

 

Пример. Независимые случайные величины Х и У заданы следующими законами распределения:

 

Х	5	2	4		У	7	9
р	0,6	0,1	0,3		g	0,8	0,2

 

Найти математическое ожидание ХУ.

 

Решение.

Найдём математические ожидания каждой из данных величин:

М(Х) = 5·0,6 + 2·0,1 + 4·0,3 = 4,4

М(У) = 7·0,8 + 9·0,2 = 7,4

Тогда М(ХУ) = 4,4·7,4 = 32,56.

Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: М(Х + У) = М(Х) + М(У) .

 

Следствие: Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.

 

Пример. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.

Решение.

Обозначим число очков, которое может выпасть на первой кости, через Х, на второй – У. Возможные значения этих величин одинаковы и равны 1, 2, 3, 4, 5, 6, причём вероятность каждого из них равна 1/6.

Найдём М числа очков, которые могут выпасть на первой кости:

42

М(Х) = 1·1/6 + 2·1/6 + 3·1/6 + 4·1/6 + 5·1/6 + 6·1/6 = 7/2

М(У) = 7/2 аналогично.

Искомое М: М(Х + У) = 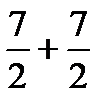= 7.

Для биномиального распределения:

    Теорема: Математическое ожидание М(Х) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: М(Х) = np

Пример. Вероятность попадания в цель при стрельбе из орудия р = 0,6. Найти М общего числа попаданий, если будет произведено 10 выстрелов.

М(Х) = np = 10·0,6 = 6 (попаданий).