Формула полной вероятности.
Сложение вероятностей несовместных событий.
Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, либо В, или обоих этих событий.
Например, из орудия произведены 2 выстрела и А – попадание в первом, В – во втором. Тогда А + В – попадание при первом выстреле, или при втором.
Определение. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Пусть события А и В – несовместные. Как найти вероятность наступления либо события А, либо В?
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А + В) = Р(А)+ Р(В).
Доказательство.
Введём обозначения:
n – общее число возможных элементарных исходов испытания;
m1 – число благоприятных исходов для события А;
m2 – число благоприятных исходов для события В.
Число благоприятных исходов для наступления либо события А, либо В, равно m1 + m2 (по правилу суммы комбинаторики).
Следовательно,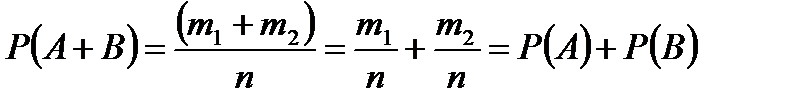 
.
Следствие.
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р(А1 + А2 + А3 + . . . + Аn) = Р(А1) + Р(А2) + Р(А3) + . . . + Р(Аn) .
Пример. В корзине 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Цветные шары – либо красный, либо синий.
Красный: Р(А) =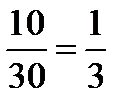 
.
Синий: Р(В) =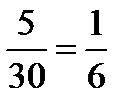 
.
18
События А и В – несовместны, поэтому теорема применима
Р(А + В) = Р(А) + Р(В) =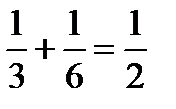 
.
Ответ: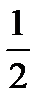 
Теорема. Сумма вероятностей событий А1 , А2 , ... Аn, образующих полную группу, равна 1: Р(А1) + Р(А2) + . . . + Р(Аn) = 1.
Доказательство.
Т.к. появление одного из событий полной группы достоверно, а вероятность достоверного события равна 1, то:
Р(А1) + Р(А2) + . . . + Р(Аn) = 1. (1)
Любые два события полной группы несовместны, поэтому можно применить теорему сложения:
Р(А1 + А2 + . . . + Аn) = Р(А1) + Р(А2) + . . . + Р(Аn) . (2)
Сравнивая теперь (1) и (2), получаем: Р(А1) + Р(А2) + . . . + Р(Аn) = 1.
Пример. Фирма получает постоянно пакеты с документами из своих филиалов, расположенных в городах А, В и С.
Вероятность получения пакета из А = 0,7; вероятность получения пакета из В = 0,2. Найти вероятность получения пакета из С.
Решение.
События «получение пакетов» образуют полную группу, поэтому 0,7 + 0,2 + Р(С) = 1. Отсюда: Р(С) = 0,1.
Ответ: Р(С)=0,1.
Противоположные события
Противоположными называют два единственно возможных события, образующих полную группу. Если событие обозначить А, то противоположное ему –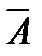 
.
Пример. 1. Попадание и промах при выстреле по цели – противоположные события.
2. Извлечение из ящика с деталями стандартной или нестандартной детали – событие противоположные.
19
Теорема. Сумма вероятностей противоположных событий равна 1. Р(А) + Р( 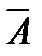) = 1 или p + q = 1.
Доказательство.
Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу равна 1.
Пример. Вероятность того, что день будет дождливым равна 0,7.
Найти вероятность того, что день будет ясным.
Решение.
События противоположные, поэтому: q = 1 – p = 0,3.
Ответ: q=0,3.
Умножение вероятностей.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.
Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годная и окрашенная.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
Например, если А, В, С – появление герба соответствует в 1, 2, 3 испытаниях, то АВС – выпадение герба во всех трех испытаниях.
Введём понятие условной вероятности.
До сих пор мы говорили о безусловной вероятности: вероятности случайного события, которое может произойти, а может не произойти при совокупных определенных условий.
Если кроме этой совокупности условий налагаются дополнительные условия, то вероятность события называют условной.
Например, вычисляют вероятность события В при дополнительном условии, что событие А уже произошло.
Пример. В урне 3 белых и три черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно.
Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечён черный шар (событие А).
20
Решение.
После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность:
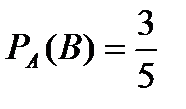
Этот же результат можно получить по формуле:
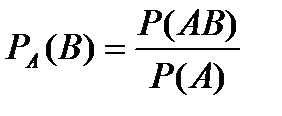(Р(А) > 0)
Действительно, вероятность появления белого шара при первом испытании:
Р(А)=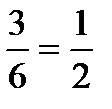 
Найдем вероятность Р(АВ) того, что в первом испытании появится черный шар, а во втором белый.
Общее число исходов – совместного появления двух шаров, безразлично какого цвета, равно числу размещений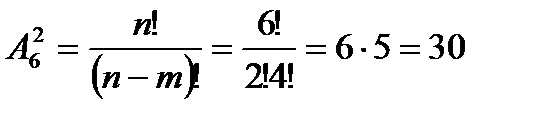 
Из этого числа исходов событию АВ благоприятствуют 3∙3=9 исходов. Следовательно, Р(АВ)=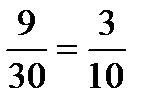 
Искомая условная вероятность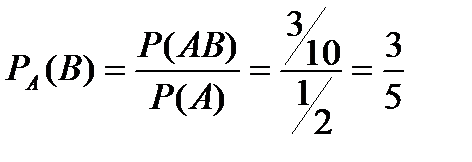 
Как видим, получен прежний результат.
Рассмотрим непосредственно теорему умножения вероятностей.
Пусть даны два события А и В, и вероятности Р(А) и Р(В) – известны.
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ) = Р(А) · РА(В).
Следствие.
Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причём вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
Р(А1 А2 А3 . . . Аn) = Р(А1) Р А1 (А2) Р А1А2 (А3) . . . + Р А1А2…Аn-1 (Аn) .
21
Пример. У сборщика имеется 3 конусных и 7 эллиптических валов. Он взял один вал, затем – второй.
Найти вероятность того, что первый из взятых валов – конусный, а второй – эллиптический.
Решение.
Вероятность, что вал конусный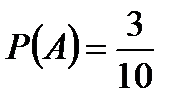 
.
Вероятность, что второй вал – эллиптический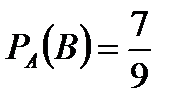 
.
Искомая вероятность: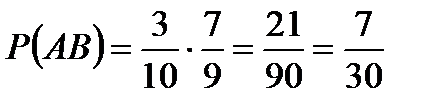 
.
Для независимых событий теорема умножения имеет вид:
Р(АВ) = Р(А) · Р(В).
Дата: 2018-11-18, просмотров: 365.
