Теорема. Вероятность появления хотя бы одного из событий 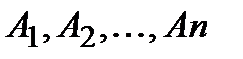 , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 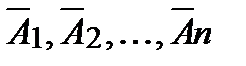 :
:
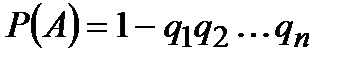
В частности, если все n событий имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий:
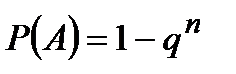
Примеры решения задач:
1. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причём 5 из них в переплёте. Наудачу берут 3 учебника.
Найти вероятность того, что хотя бы один из взятых учебников окажется в переплёте (событие А).
Решение
Первый способ
Событие А будет осуществлено, если произойдёт любое из следующих трёх несовместных событий: событие В – один учебник в переплёте, два – без переплёта, или событие С – два учебника в переплёте, один без переплёта, или событие D – три учебника в переплёте.
22
Событие А (хотя бы один из трёх взятых учебников в переплёте) можно представить в виде суммы этих событий:
А = В + С + D.
Тогда по теореме сложения вероятностей несовместных событий:
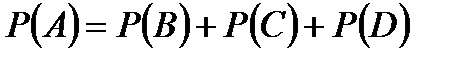 (*)
(*)
Найдём вероятности событий В, С и D:
а) 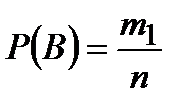
n – одинаково для всех событий
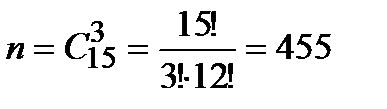
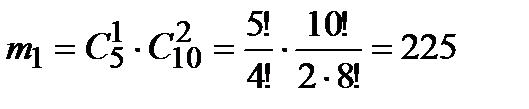
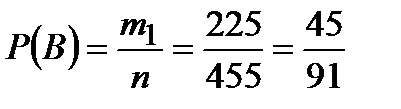
б) 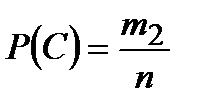
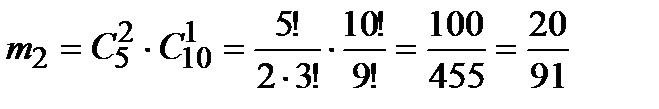
в) 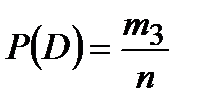
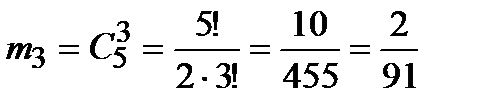 .
.
Подставив эти вероятности в равенство (*), окончательно получим:
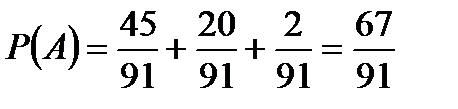 .
.
Второй способ
Воспользуемся теоремой: сумма вероятностей противоположных событий равна единице.
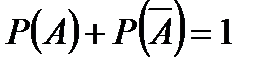
В нашем случае событие А – хотя бы один из взятых трёх учебников имеет переплёт; событие  – ни один из взятых учебников не имеет переплёта. Эти события противоположные и тогда:
– ни один из взятых учебников не имеет переплёта. Эти события противоположные и тогда:
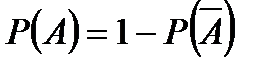
Вероятность появления 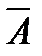 (ни один из взятых учебников не имеет переплёта):
(ни один из взятых учебников не имеет переплёта):
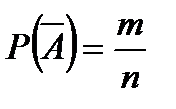 ;
;
23
n = 455; m = 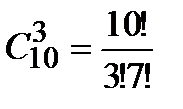
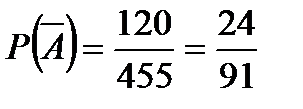 ;
;
Искомая вероятность
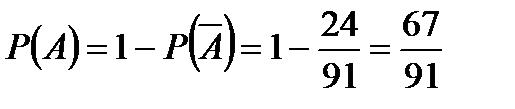 .
.
Ответ: 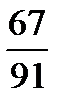
2. Вероятность того, что стрелок при одном выстреле попадает в мишень равна р = 0,9. Стрелок произвёл 3 выстрела.
Найти вероятность того, что все 3 выстрела дали попадание.
Решение
р=р∙р∙р=0,9∙0,9∙0,9=0,729
Ответ: р = 0,729.
3. В читальном зале имеется 6 учебников, из которых 3 в переплёте. Библиотекарь наудачу взял 2 учебника.
Найти вероятность того, что оба учебника окажутся в переплёте.
Решение
Введём обозначения событий:
А – первый взятый учебник имеет переплёт;
В – второй учебник имеет переплёт;
Вероятность того, что первый учебник имеет переплёт:
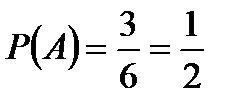 .
.
Вероятность того, что второй учебник имеет переплёт, при условии, что первый взятый учебник был в переплёте, т.е. условная вероятность события В:
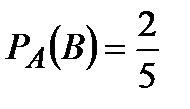 .
.
Искомая вероятность того, что оба учебника имеют переплёт, по теореме умножения вероятностей зависимых событий равна:
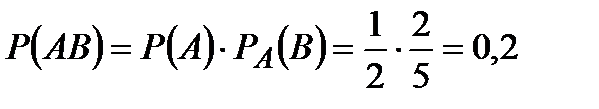
Ответ: 0,2.
4. Для некоторой местности среднее число пасмурных дней в июле равно шести.
Найти вероятность того, что первого и второго июля будет ясная погода.
24
Решение
Р(А)= 
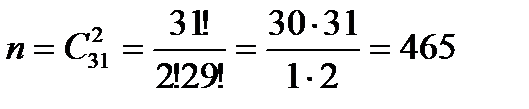
Р(А)= 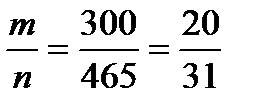
Ответ: р = 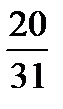
5. В электрическую цепь последовательно включены 3 элемента, работающие независимо один от другого. Вероятность отказов первого, второго и третьего элементов соответственно равны:
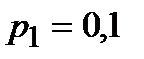 ;
; 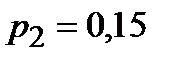 ;
; 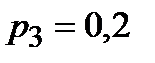 .
.
Найти вероятность того, что тока в цепи не будет.
Решение
Так как элементы включены последовательно, то тока в цепи не будет (событие А), если откажет хотя бы один из элементов. Тогда искомая вероятность:
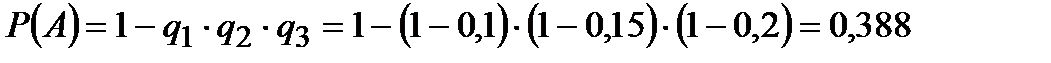
Ответ: 0,388.
6. Вероятности попадания в цель при стрельбе из трех орудий таковы:
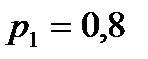 ;
; 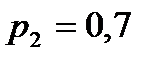 ;
; 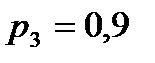 .
.
Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение
Вероятности попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события 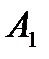 (попадание первого орудия),
(попадание первого орудия), 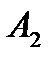 (попадание второго орудия) и
(попадание второго орудия) и 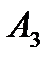 (попадание третьего орудия) независимы в совокупности.
(попадание третьего орудия) независимы в совокупности.
Вероятности событий противоположных событиям 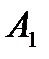 ,
, 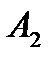 и
и 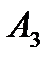 (т,е, вероятности промахов), соответственно равны:
(т,е, вероятности промахов), соответственно равны:
25
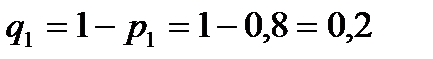
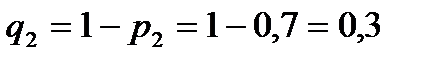
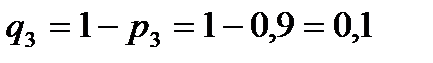
Искомая вероятность: 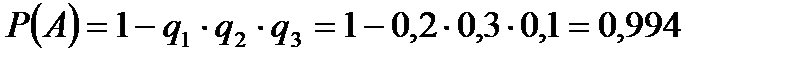
Ответ: 0,994
6. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Решение
Обозначим через А событие «при n выстрелах стрелок попадает в цель хотя бы один раз». События, состоящие в попадании в цель при первом, втором выстрелах и т.д., независимы в совокупности, поэтому:
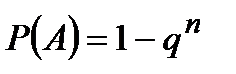
Приняв во внимание, что по условию, Р(А) ≥ 0,9; р=0,4 (q=1-0,4 =0,6), получим 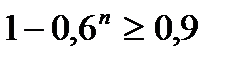 , следовательно
, следовательно 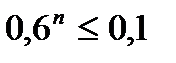
Прологарифмируем это неравенство по основанию 10:
n∙lg0,6 ≤ lg0,1
Отсюда, учитывая, что lg0,6 < 0, имеем
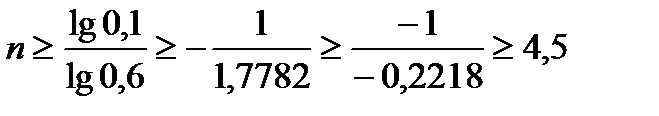
Итак, n ≥ 5.
Ответ: стрелок должен произвести не менее 5 выстрелов.
Задачи для самостоятельного решения:
1. В парк прибыли 5 трамваев и 7 троллейбусов. Через некоторое время отъехали 4 транспортных средства.
Найти вероятность того, что среди них не менее трёх трамваев.
Ответ: р = 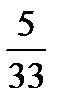
3. Брошены монета и игральная кость.
Найти вероятность совмещения событий: «появился герб» и «появилось 6 очков».
Ответ: р = 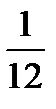
26
4. Для разрушения моста достаточно попадания одной авиационной бомбы.
Найти вероятность того, что мост будет разрушен, если на него сбросить три бомбы, вероятности попадания которых соответственно равны: 0,6; 0,5; 0,4.
Ответ: р = 0,88
5. В студии 4 кинокамеры. Для каждой камеры, вероятность того, что она включена в данный момент, равна р = 0,7.
Найти вероятность того, что в данный момент включена хотя бы одна камера.
Ответ: р = 0,9919
6. Три электрические лампочки последовательно включены в цепь. Вероятность того, что при повышении напряжения выше номинального тока в цепи не будет, равна 0,936.
Найти вероятность того, что при повышенном напряжении перегорит одна (любая) лампочка.
Ответ: р = 0,6
7. Вероятность того, что при одном выстреле стрелок попадёт в десятку, равна 0,6. Сколько выстрелов должен сделать стрелок, чтобы с вероятностью не менее 0,8 он попал в десятку хотя бы один раз?
Ответ: n 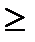 2
2
Вопросы для самопроверки:
1. Теорема сложения вероятностей. Её доказательство.
2. Следствие теоремы сложения вероятностей.
3. Теорема о вероятности полной группы событий.
4. Противоположные события, теорема о сумме вероятностей противоположных событий.
5. Понятие условной вероятности.
6. Теорема умножения вероятностей.
7. Следствие теоремы умножения вероятностей.
8. Независимые события. Вычисление вероятности наступления хотя бы одного независимого события.
27
Повторение испытаний.
1. Формула Бернулли.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся, что вероятность события А в каждом испытании одна и та же и равна р. Следовательно, вероятность ненаступления события постоянна и равна q.
q = 1 – p
Поставим перед собой задачу вычислить вероятность того, что при n испытаниях событие А осуществится k раз и не осуществится n – k раз.
Искомую вероятность обозначим Рn(k). Например, Р5(3) – событие в 5 испытаниях появляется 3 раза и не появится 2 раза.
Поставленную задачу можно решить с помощью формулы Бернулли.
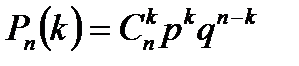
|
Пример. Вероятность того, что расход электроэнергии в продолжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение
р =0,75, вероятность перерасхода q = 1 – 0,75 = 0,25. Р6(4) = 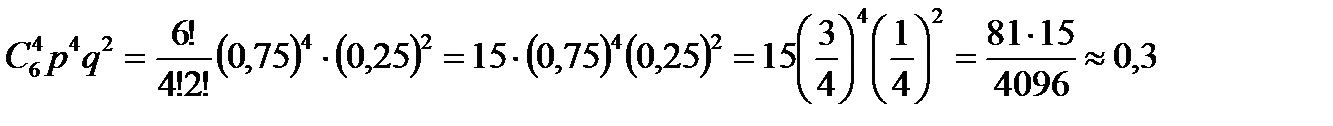
2. Локальная теорема Лапласа.
Пользоваться формулой Бернулли при больших значениях n затруднено, т.к. надо производить действия над громадными числами. Поэтому есть другая формула, которая позволяет найти вероятность появления события k раз в n испытаниях, если число испытаний велико.
Это формула Лапласа.
Теорема. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рn(k) того, что событие А появится в n испытаниях ровно k раз, равна:
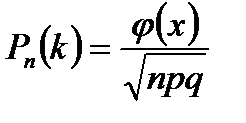 при х =
при х = 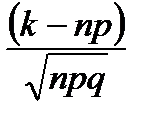
28
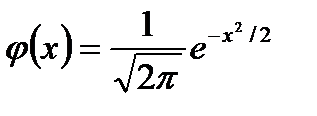
|
Имеются таблицы, в которых находятся значения функции φ(х), соответствующие положительным значениям аргумента. Для отрицательных значений пользуются теми же таблицами, т.к. функция φ(х) – чётная, т.е. φ(–х) = φ(х).
Пример 1. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение.
n = 400
k = 80
p = 0,2
q = 0,8
По формуле Лапласа:
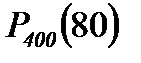 =
= 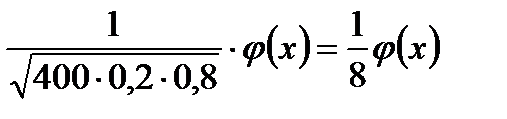
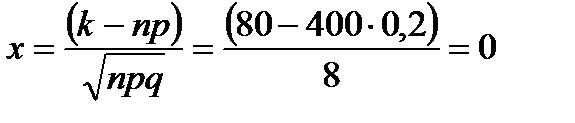
φ(0) = 0,3989
Искомая вероятность: 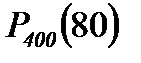 =
= 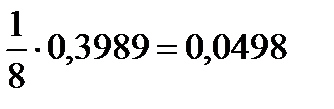 .
.
Если считать по формулам Бернулли, то 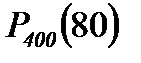 = 0,0498.
= 0,0498.
Пример 2. Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.
Решение.
n = 10
k = 8
p = 0,75
q = 0,25
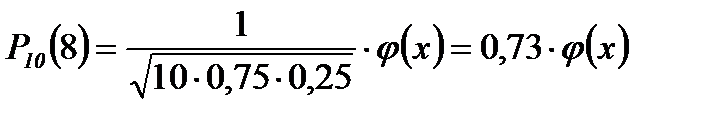
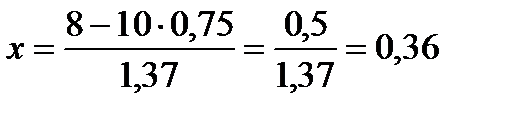
29
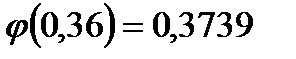
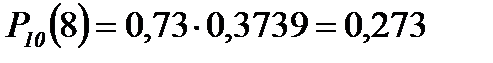
Если считать по формуле Бернулли, то получим: 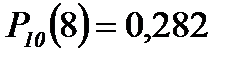 . Это ближе к истине, т.к. формула Лапласа даёт хорошие результаты при достаточно больших n.
. Это ближе к истине, т.к. формула Лапласа даёт хорошие результаты при достаточно больших n.
3. Интегральная теорема Лапласа.
Опять предположим, что проводится n испытаний, в каждом из которых вероятность появления события А постоянна и 0 < р < 1.
Как вычислить вероятность того, что событие А появится в n испытаниях не менее k1 и не более k2 раз (т.е. от k1 до k2 раз). На этот вопрос даёт ответ интегральная теорема Лапласа:
Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рn(k1 k2) того, что событие А появится в n испытаниях от k1 до k2 раз, равна:
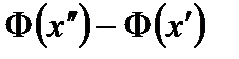 ,
,
где 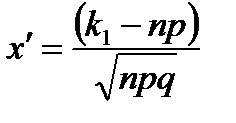 и
и 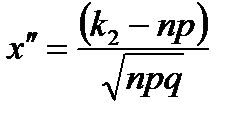 .
.
Функция 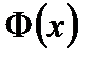 называется функцией Лапласа.
называется функцией Лапласа.
Есть таблицы, где вычислены и приводятся её значения, для положительных значений аргумента. Для отрицательных значений пользуются той же таблицей, только надо помнить, что 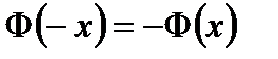 при
при 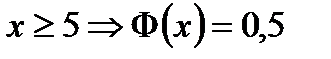 .
.
Пример. Вероятность того, что деталь не прошла проверку р = 0,2.
Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение.
p = 0,2
q = 0,8
n = 400
k1 = 70
k2 = 100
P400(70, 100) = 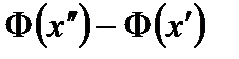
30
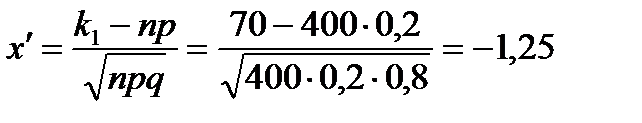
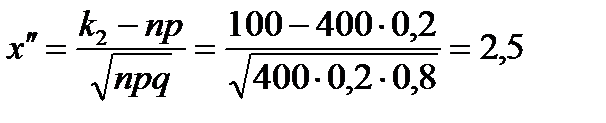
Ф(–1,25) = –0,3944
Ф(2,5) = 0,4938
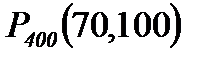 = 0,4938 + 0,3944 = 0,8882.
= 0,4938 + 0,3944 = 0,8882.
Вопросы для самопроверки:
1. Формула Бернулли. В каком случае её применяют?
2. Локальная теорема Лапласа. Отличие от формулы Бернулли. Особенности функции 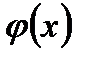 .
.
3. Интегральная теорема Лапласа. Особенности функции 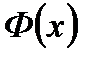 .
.
После изучения теории и решения задач из раздела 1, можно выполнять практическую работу №1.
31
Дата: 2018-11-18, просмотров: 663.