Введём понятие отклонения значений случайной величины от её математического ожидания.
Отклонением называют разность между случайной величиной и ее математическим ожиданием: Х – М(Х).
На практике часто приходится оценить рассеяние возможных значений случайной величины вокруг её среднего значения.
Например, в артиллерии – кучность снарядов вокруг поражаемой цели.
На первый взгляд, кажется, что нужно найти (для оценки рассеяния) все возможные значения отклонения случайной величины, а затем – их среднее значение. Но среднее значение отклонения равно 0 (т.к. одни возможные отклонения положительны, другие – отрицательны).
Поэтому пришли к решению заменить возможные отклонения их квадратами. Дисперсия характеризует степень рассеяния значений случайной величины от своего среднего значения и обозначается D(Х).
Дисперсией называют математическое ожидание (т.е. среднее значение) квадратов отклонений случайной величины от их среднего значения (т.е. математического ожидания)
D(Х) = М(Х – М(Х))2
Формула для расчётов:
.
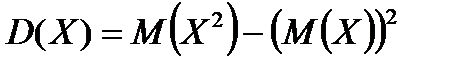Пример. Найти дисперсию случайной величины Х, которая задача следующим законом распределения:
43
| Х | 2 | 3 | 5 |
| р | 0,1 | 0,6 | 0,3 |
Решение.
М(Х) = 2·0,1 + 3·0,6 + 5·0,3 = 3,5
Закон распределения Х2:
| Х2 | 4 | 9 | 25 |
| р | 0,1 | 0,6 | 0,3 |
Найдём М(Х2) = 4·0,1 + 9·0,6 + 25·0,3 = 13,3
D(Х) = 13,3 – 3,52= 1,05.
Свойства дисперсии.
Свойство 1. Дисперсия постоянной величины С = 0.
D(C) = 0.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D(C Х) = С2D(Х).
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D(Х + У) = D(Х) + D(У) .
Следствие : Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.
Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D(Х – У) = D(Х) + D(У) .
Пример. Дисперсия случайной величины Х равна 5. Найти дисперсию следующих величин: а) х – 1; б) –2х; в) 3х + 6.
а) D (х – 1) = D (Х) + D (1) = 5;
б) D (–2х) = (–2)2·5 = 20;
в) D (3х + 6) = (3)2·5 = 45.
44
Для биномиального распределения:
Теорема. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:
D(Х) = npq.
Пример. Производится 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины Х – числа появлений события в этих испытаниях.
Решение.
q = 1 – 0,6 = 0,4
D(Х) = 10·0,4·0,6 = 2,4.
Примеры решения задач:
1. На пути движения автомашины 4 светофора, каждый из которых запрещает дальнейшее движение автомашины с вероятностью 0,5. Найти ряд распределения числа светофоров, пройденных машиной до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины?
Решение
Пусть Х – дискретная случайная величина, равная числу светофоров, пройденных автомобилем до первой остановки, она может принимать значения 0, 1, 2, 3, 4.
Случайная величина Х принимает значение равное 0, если автомобиль попал на запрещающий сигнал на первом же светофоре, вероятность этого Р(Х = 0) = 0,5.
Случайная величина Х принимает значение равное 1, если автомобиль проехал на первом светофоре и попал на запрещающий сигнал на втором светофоре, вероятность этого
Р(Х = 1) = 0,5·0,5 = 0,25.
Случайная величина Х принимает значение равное 2, если автомобиль проехал на первом и втором светофоре и попал на запрещающий сигнал на третьем светофоре, вероятность этого Р(Х = 2) = 0,5·0,5·0,5 = 0,125.
Случайная величина Х принимает значение равное 3, если автомобиль проехал на первом, втором и третьем светофоре и попал на запрещающий сигнал на четвертом светофоре, вероятность этого Р(Х = 3) = 0,5 · 0,5 · 0,5 · 0,5 = 0,54 = 0,0625.
Случайная величина Х принимает значение равное 4 если автомобиль проехал на всех 4 светофорах, вероятность этого Р(X = 4) = 0,54 = 0,0625.
45
Таким образом, закон распределения случайной величины Х имеет вид:
| хi | 0 | 1 | 2 | 3 | 4 |
| рi | 0,5 | 0,25 | 0,125 | 0,0625 | 0,0625 |
Расчеты произведены правильно, так как сумма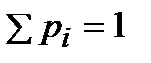 
.
Математическое ожидание:
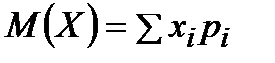= 0·0,5 + 1·0,25 + 2·0,125 + 3·0,0625 + 4·0,0625 = 0,9375.
Дисперсия:
=
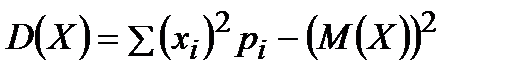= 02·0,5 + 12·0,25 + 22·0,125 + 32·0,0625 + 42·0,0625 – 0,93752 
1,434.
2. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырёх выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Найти дисперсию этой случайной величины.
Решение
Введём дискретную случайную величину Х – (число промахов) Х – может принимать значения 0, 1, 2, 3, 4.
Найдём соответствующие вероятности.
Х = 0, если охотник попал в дичь при первом выстреле, поэтому Р(Х = 0) = 0,7.
Х = 1, если охотник не попал в дичь при первом выстреле и попал в дичь при втором выстреле, поэтому Р(Х = 1) = 0,3·0,7 = 0,21.
Х = 2, если охотник не попал в дичь при первом выстреле и втором выстреле, и попал в дичь при третьем выстреле, поэтому Р(Х = 2) = 0,3·0,3·0,7 = 0,063.
Х = 3, если охотник не попал в дичь при первом, втором и третьем выстрелах, и попал в дичь при четвёртом выстреле, поэтому Р(Х = 3) = 0,3·0,3·0,3·0,7 = 0,0189.
Х = 4, если охотник не попал в дичь при первом, втором, третьем и четвёртом выстрелах, поэтому Р(Х = 4) = 0,3·0,3·0,3·0,3·0,7 = 0,0081.
Закон распределения случайной величины Х имеет вид:
| хi | 0 | 1 | 2 | 3 | 4 |
| рi | 0,7 | 0,21 | 0,063 | 0,0189 | 0,0081 |
46
Найдём числовые характеристики дискретной случайной величины Х:
Математическое ожидание:
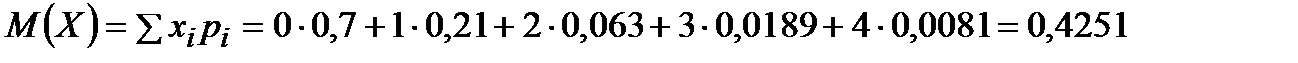
Дисперсия:
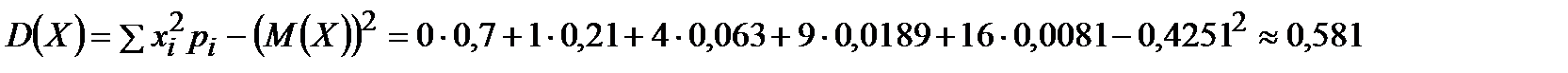
Вопросы для самопроверки:
1. Что такое математическое ожидание?
2. Чему равно математическое ожидание числа появления события в одном испытании?
3. Вероятностный смысл математического ожидания.
4. Свойства математического ожидания (4 свойства).
5. Что такое независимые случайные величины?
6. Что понимают под произведением независимых случайных величин? Чему равны вероятности значений ХУ?
7. Что такое сумма независимых случайных величин?
8. Математическое ожидание числа появления события в n независимых испытаниях?
9. Отклонение случайной величины от её математического ожидания – что это?
10. Что характеризует дисперсия?
11. Свойства дисперсии (4 свойства).
12. Дисперсные числа появления события в n независимых испытаниях.
После изучения теории и решения задач из раздела 2, можно выполнять практическую работу №2.
После выполнения и защиты практических работ №1 и №2, можно выполнять контрольную работу.
47
Дата: 2018-11-18, просмотров: 421.
