Пусть известно статистическое распределение частот количественного признака Х. (Количественный признак, например, контролируемый размер детали).
nх – число наблюдений, при которых наблюдалось значение признака меньшее х;
n – общее число наблюдений (объем выборки).
Относительная частота события Х < х = 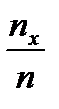 .
.
Если изменяется х, то изменяется и 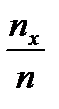 , т.е. она есть функция от х. Так как эта функция находится опытным (эмпирическим) путём, то её называют эмпирической.
, т.е. она есть функция от х. Так как эта функция находится опытным (эмпирическим) путём, то её называют эмпирической.
Определение. Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(х), определяющую для каждого значения х относительную частоту события Х < х.
53
Итак, по определению: 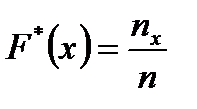
где nх – число вариант, значения которых меньше х
n – объем выборки.
Например, чтобы найти F *(х2), надо число вариант меньшее х2 разделить на n: 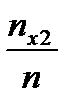 .
.
Функцию распределения F(х), генеральной совокупности называют теоретической функцией распределения. Она нам известна как интегральная функция распределения. Различие между F *(х) и F(х) состоит в том, что F(х) определяет вероятность события Х < х, а F *(х) – определяет относительную частоту этого же события. Но W → р и чем больше n , тем меньше различие. Поэтому целесообразно использовать эмпирическую функцию распределения выборки для приближённого представления интегральной функции распределения генеральной совокупности.
Функция F *(х) обладает всеми свойствами функции F(х):
1) Значения F *(х) принадлежат отрезку [0,1].
2) F *(х) – неубывающая функция.
3) Если х1 – наименование варианта, то F *(х) = 0, 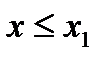 ; если хk – наибольшая варианта, то F *(х) = 1, х > хk
; если хk – наибольшая варианта, то F *(х) = 1, х > хk
Следовательно, эмпирическая функция распределения выборки служит для оценки теоретической (интегральной) функции распределения генеральной совокупности.
Пример: Построить эмпирическую функцию по данному распределению выборки:
| хi | 2 | 6 | 10 |
| ni | 12 | 18 | 30 |
Решение.
Объем выборки n = 60.
1. хmin = 2, следовательно F *(х) = 0, 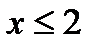 .
.
2. Значение х < 6, а именно х1 = 2 наблюдалось12 раз, следовательно F *(х) = 12/60 = 0,2 при 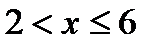 .
.
3. Значение х < 6 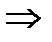 х1 = 2, х2 = 6, наблюдались 12 + 18 раз, F *(х) = 30/60 = 0,5 при
х1 = 2, х2 = 6, наблюдались 12 + 18 раз, F *(х) = 30/60 = 0,5 при 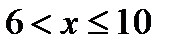 .
.
4. хmax = 10 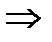 F *(х) = 1, х > 10.
F *(х) = 1, х > 10.
54
Искомая эмпирическая функция: 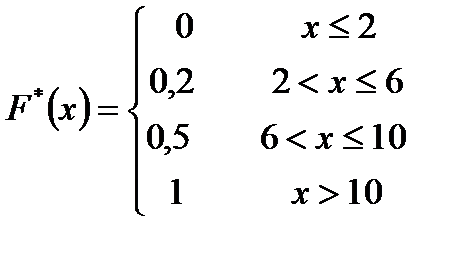 .
.
График этой функции изображён на рисунке.
F *(х)
1
0,5
0,2
2 4 6 8 10 12 х
В общем виде формула для вычисления F *(х) выглядит следующим образом:
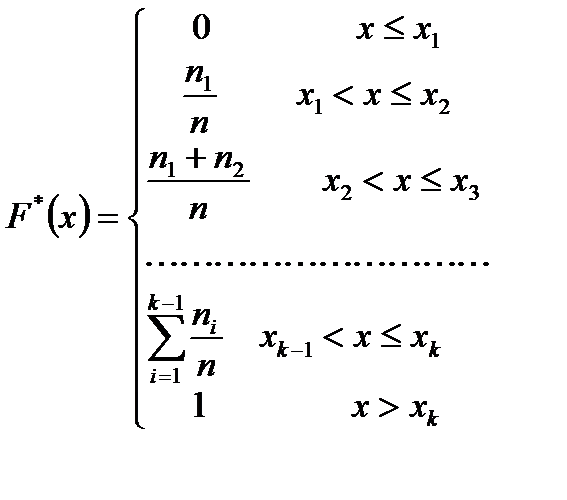
Вопросы для самопроверки:
1. Каковы основные задачи математической статистики?
2. Что такое выборка?
3. Определение и построение полигона частот.
4. Определение и построение гистограммы частот.
5. Эмпирическая функция распределения, расчёт и построение графика.
После изучения теории и решения задач из раздела 1, можно выполнять практическую работу №1.
55
Приложение.
Студент выполняет тот вариант, который совпадает с его номером в журнале.
| номер в журнале | номер варианта |
| 1, 11, 21, 31 | 1 |
| 2, 12, 22, 32 | 2 |
| 3, 13, 23, 33 | 3 |
| 4, 14, 24, 34 | 4 |
| 5, 15, 25, 35 | 5 |
| 6, 16, 26 | 6 |
| 7, 17, 27 | 7 |
| 8, 18, 28 | 8 |
| 9, 19, 29 | 9 |
| 10, 20, 30 | 10 |
Практическая работа № 1.
Дата: 2018-11-18, просмотров: 491.