Цель работы: «Освоение применения комбинаторных формул для расчета вероятностей».
Задание 1.
Рассчитать вероятность события с помощью формулы классического определения вероятности: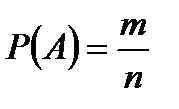 
.
56
Задания 2, 3.
Рассчитать вероятность события, используя формулы комбинаторики и основные теоремы теории вероятностей.
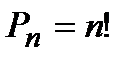– перестановки,
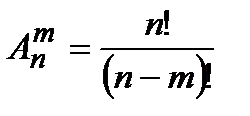– размещения,
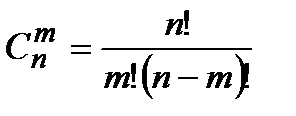– сочетания.
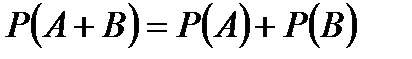– формула сложения вероятностей,
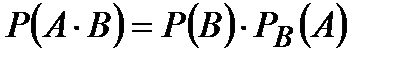– формула умножения вероятностей,
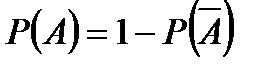– вероятность события, рассчитанная через вероятность противоположного события.
Вариант 1
Задача 1.
Бросают две монеты. Найти вероятность того, что:
а) на обеих монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) меньше, чем 2 белых шара;
в) хотя бы один белый шар.
Задача 3.
Вероятность того, что событие появится хотя бы один раз в трех независимых испытаниях, равна 0,936.
Найти вероятность появления события в одном испытании (предполагается, что во всех испытаниях вероятность появления события одна и та же).
Вариант 2
Задача 1.
Бросают три монеты. Найти вероятность того, что:
а) на всех монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
57
а) 3 белых шара;
б) меньше, чем 3 белых шара;
в) хотя бы один белый шар.
Задача 3.
В типографии имеется 4 печатные машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9.
Найти вероятность того, что в данный момент работает хотя бы одна машина.
Вариант 3
Задача 1.
Бросают четыре монеты. Найти вероятность того, что:
а) на всех монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 6 черных и 5 белых шаров. Случайным образом вынимают 4 шара.
Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) меньше, чем 2 белых шара;
в) хотя бы один белый шар.
Задача 3.
У сборщика имеется 16 деталей, изготовленных заводом № 1, и 4 детали, изготовленные заводом № 2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом № 1.
Вариант 4
Задача 1.
Бросают две игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:
а) только чётные;
б) одно чётное, другое нечётное;
в) сумма которых делится на три.
Задача 2.
В урне содержатся 7 чёрных и 4 белых шара. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) меньше, чем 2 белых шара;
в) хотя бы один белый шар.
Задача 3.
Брошена монета и игральная кость. Найти вероятность совмещения событий «появился орел», «появилось 6 очков».
58
Вариант 5
Задача 1.
Бросают две игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:
а) только нечётные;
б) одно нечётное, другое чётное;
в) сумма которых делится на четыре.
Задача 2.
В урне содержатся 8 чёрных и 6 белых шаров. Случайным образом вынимают 5 шаров.
Найти вероятность того, что среди них имеется:
а) три белых шара
б) меньше, чем 3 белых шара
в) хотя бы один белый шар.
Задача 3.
Вероятность того, что при одном выстреле стрелок выбьет 10 очков, равна 0,1; вероятность выбить 9 очков 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.
Вариант 6
Задача 1.
Бросают 3 игральные кости. Найти вероятность того, что на верхних гранях появятся
следующие числа очков:
а) только чётные;
б) которые все одинаковы;
в) хотя бы на одной из костей появится 6 очков.
Задача 2.
В урне содержатся 6 чёрных и 7 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) три белых шара;
б) меньше, чем 3 белых шара;
в) хотя бы один белый шар.
Задача 3.
События А, В, С, D образуют полную группу. Вероятности событий таковы: Р(А) = 0,1; Р(В) = 0,4; Р(С) = 0,3. Чему равна вероятность события D?
59
Вариант 7
Задача 1.
Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится:
а) только нечетные;
б) которые все одинаковы;
в) хотя бы на одной из костей появится 4 очка.
Задача 2.
В урне содержится 8 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 3 белых шара;
б) меньше, чем 3 белых шара;
в) хотя бы один белый шар.
Задача 3.
Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в 1-ю область равна 0,45, во 2-ю – 0,35. Найти вероятность того, что стрелок при одном выстреле попадает либо в первую, либо во вторую область.
Вариант 8
Задача 1.
Бросают три монеты. Найти вероятность того, что:
а) на всех монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 8 белых и 6 черных шаров. Случайным образом вынимают 5 шаров.
Найти вероятность того, что среди них имеется:
а) 2 белых шара
б) меньше, чем 2 белых шара
в) хотя бы один белый шар
Задача 3.
В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А) при втором – чёрный (событие В) и при третьем – синий (событие С).
60
Вариант 9
Задача 1.
Бросают две монеты. Найти вероятность того, что:
а) на обеих монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 7 белых и 5 черных шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 3 белых шара
б) меньше, чем 3 белых шара
в) хотя бы один белый шар
Задача 3.
При стрельбе из винтовки относительная частота попадания в цель, оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов.
Вариант 10
Задача 1.
Брошены две монеты. Найти вероятность того, что:
а) на обеих монетах появился орел;
б) хотя бы на одной монете появился орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 5 белых и 6 черных шаров. Случайным образом вынимают 3 шара. Найти вероятность того, что среди них имеется:
а) 2 белых шара
б) меньше, чем 2 белых шара
в) хотя бы один белый шар
Задача 3.
В студии телевидения 3 камеры. Для каждой вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера.
61
Практическая работа № 2.
Дата: 2018-11-18, просмотров: 442.
