Дадим количественную оценку возможности наступления того или иного события.
Пример: Пусть в корзине имеется 6 шаров: 2 – красных, 3 – синих, 1 – белый. Возможность вынуть цветной шар больше, чем белый. Можно охарактеризовать эту возможность числом, которое называют вероятностью. Следовательно, вероятность есть число, которое характеризует степень возможности появления события.
8
Поставим задачу оценить вероятность появления цветного шара.
Обозначим это событие – А.
Испытание – извлечение шара.
Результат испытания – элементарный исход (событие).
Обозначим их:
| ω1 | ω2 ω3 | ω4 ω5 ω6 | ||
| белый | красный | синий |
Эти исходы образуют полную группу попарно несовместных событий – появится только один шар – и они равно возможны.
Те элементарные исходы, при которых наступает интересующее нас событие, благоприятные события: у нас – ω2 ω3 ω4 ω5 ω6.
Отношение числа благоприятных исходов события А к их общему числу, называется вероятностью события А. Обозначается Р(А).
В нашем примере: Р(А) = 5/6. Запишем теперь определение вероятности.
Вероятностью события А называют отношение числа благоприятных для события исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Р(А) = m/n,
где m – число элементарных исходов, благоприятных для события А;
n – число всех возможных элементарных исходов испытаний.
Свойства вероятности.
а) Вероятность достоверного события равна 1.
Действительно, каждый элементарный исход является благоприятным для события А, т.е. m = n Р(А) = 1.
б) Вероятность невозможного события равна 0.
Т.е. m = 0 и Р(А) = 0/n = 0.
в) Вероятность случайного события есть положительное число, заключённое между 0 и 1.
0 < m < n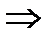 
0 < 
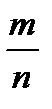< 1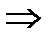 
0 < Р(А) < 1
Следовательно, вероятность любого события удовлетворяет следующему неравенству:
| 0 ≤ Р(А) ≤ 1 |
9
Примеры решения задач:
1. Набирая номер телефона, абонент забыл одну цифру и набрал её наудачу.
Найти вероятность того, что набрана нужная цифра.
Решение
Событие А – набрана нужная цифра.
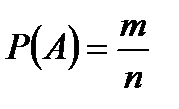; n = 10 m = 1 (нужная цифра лишь одна).
.
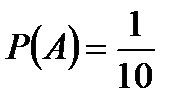Ответ: Р(А)=0,1.
2. В ящике 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь.
Найти вероятность того, что извлечённая деталь окажется окрашенной.
.
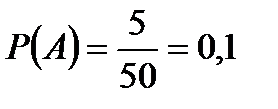Ответ: Р(А) = 0,1.
3. Брошена игральная кость.
Найти вероятность того, что выпадет чётное число очков.
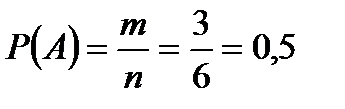
Ответ: Р(А) = 0,5
4. Участники жеребьёвки тянут из ящика жетоны с номерами от 1 до 100.
Найти вероятность того, что номер первого наудачу извлечённого жетона не содержит цифры 5.
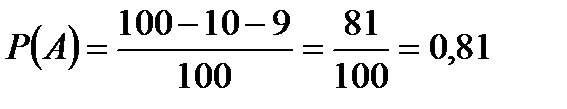
Ответ: р = Р(А)= 0,81.
5. Брошены 2 игральные кости.
Найти вероятность того, что сумма очков на выпавших гранях равна семи.
m=6 (1+6; 2+5; 3+4; 4+3; 5+2; 6+1)
n= 
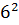=36 (6 – граней на одной кости; 2 – количество костей).
10
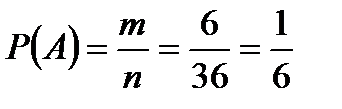
Ответ: р = Р(А)=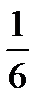 
6. Брошены 2 игральные кости.
Найти вероятность того, что сумма очков на выпавших гранях равна пяти, а произведение – четырём.
m=2 (1+4; 4+1)
n= 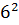=36 (6 – граней на одной кости; 2 – количество костей).
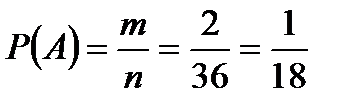
Ответ: р = Р(А)=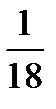 
Задачи для самостоятельного решения:
1. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем перемешаны.
Найти вероятность того, что наудачу извлечённый кубик будет иметь сокращённых граней:
| а) одну | б) две | в) три |
Ответ: а) 0,384; б) 0,096; в) 0,008
2. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость.
Найти вероятность того, что вторую наудачу извлечённую кость можно приставить к первой, если первая кость:
а) оказалась дублем;
б) не есть дубль.
Ответ: а)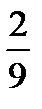 
; б)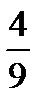 
.
3. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: О, П, Р, С, Т.
11
Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно прочесть слово «СПОРТ».
Ответ: р =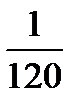 
4. На каждой из шести одинаковых карточек напечатана одна из следующих букв: А, Т, М, Р, С, О. Карточки перемешаны.
Найти вероятность того, что на четырёх, вынутых по одной и расположенных «в одну линию» карточках можно прочесть слово «ТРОС».
Ответ: р =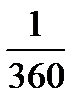 
Комбинаторные формулы.
При подсчёте вероятностей большую пользу оказывают формулы комбинаторики:
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества.
Перестановки – комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.
Число возможных перестановок:
Рn = n!
где n! = 1∙2∙3∙. . . ∙n.
Пример. Даны цифры 1, 2, 3. Сколько трехзначных чисел можно составить из них, если каждая цифра входит в изображение числа 1 раз?
Р3 = 3n! = 1∙2∙3 = 6.
Размещения – комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.
Число всех возможных размещений:
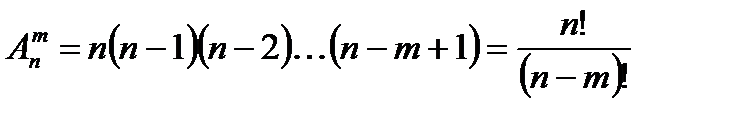
Пример. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
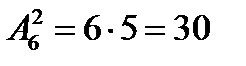
12
Сочетания – комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.
Число сочетаний: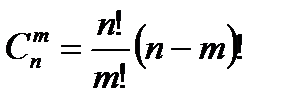 
Пример. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Искомое число: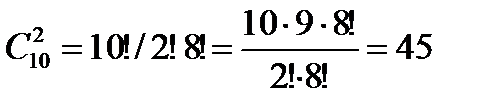 
.
Числа размещений, перестановок и сочетаний связаны равенством:
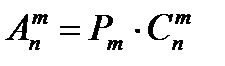
При решении задач комбинаторики существуют следующие правила:
Правило суммы:
Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В – n способами, то выбрать либо А, либо В можно m + n способами.
Правило произведения:
Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.
Примеры решения задач:
1. В ящике содержится 10 одинаковых деталей, помеченных номерами от 1 до 10. Наудачу извлечено 6 деталей.
Найти вероятность того, что среди извлечённых деталей окажется деталь № 1.
Решение
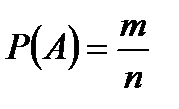
n – общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из десяти:
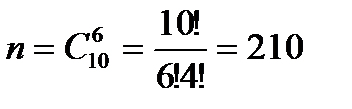
m – число исходов, благоприятных для интересующего нас события: среди отобранных шести деталей есть деталь № 1, и, следовательно, остальные 5
13
деталей имеют другие номера. Число таких исходов равно числу способов, которыми можно отобрать 5 деталей из оставшихся девяти:
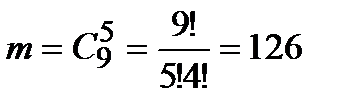
Тогда искомая вероятность:
;
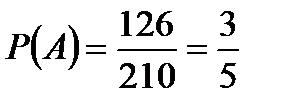Ответ: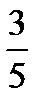 
2. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу вынимает три детали.
Найти вероятность того, что извлечённые детали окажутся окрашенными.
Решение
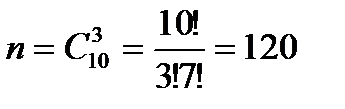
способами можно вынуть три окрашенные детали из десяти.
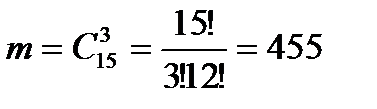
способами можно вынуть три неокрашенные детали из пятнадцати.
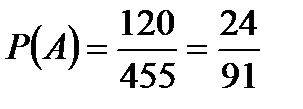
Ответ: р =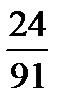 
3. Набирая номер телефона, абонент забыл последние три цифры, и, помня, что эти цифры различны, набрал их наудачу.
Найти вероятность того, что набраны нужные цифры.
Решение
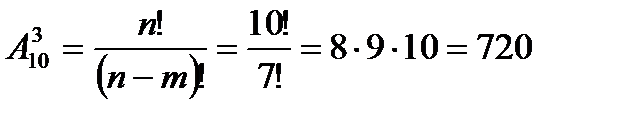
р =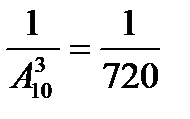 
Ответ: р =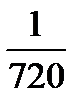 
14
4. У Васи живут четыре кота.
а) сколькими способами можно рассадить котов по углам комнаты?
Решение
В задаче речь идёт о разных объектах! Наказанию подвергаются сразу все коты, плюс важно их расположение, поэтому здесь имеют место перестановки.
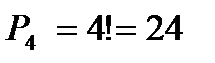
Ответ: 24 способами можно рассадить котов по углам комнаты.
б) сколькими способами можно отпустить гулять котов?
Решение
Предполагается, что коты ходят гулять только через дверь, при этом вопрос подразумевает безразличие по поводу количества животных – на прогулку могут выйти 1, 2, 3 или 4 кота.
Составляем все возможные сочетания:
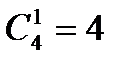способами можно отпустить гулять одного кота (любого из четырёх).
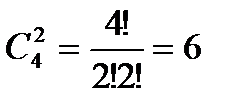способами можно отпустить гулять двух котов.
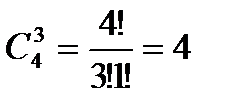способами можно отпустить гулять трех котов (какой-то один из четырех сидит дома.
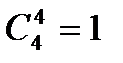способом можно выпустить всех котов.
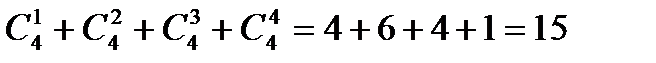
Ответ: 15 способами можно отпустить гулять котов.
в) сколькими способами Вася может взять на руки двух котов (одного – на левую, другого на правую)?
Решение
Ситуация предполагает не только выбор двух котов, но и их размещение по рукам:
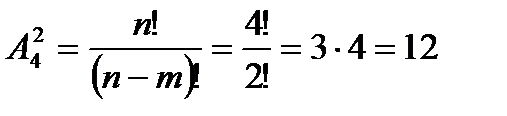
Ответ: 15 способами можно взять на руки двух котов.
5. Боря, Дима и Володя сели играть в «очко». Сколькими способами им можно сдать по одной карте из колоды в 36 карт?
15
Решение
Здесь важно не только то, какие 3 карты будут извлечены из колоды, но и то, как они будут распределены между игроками.
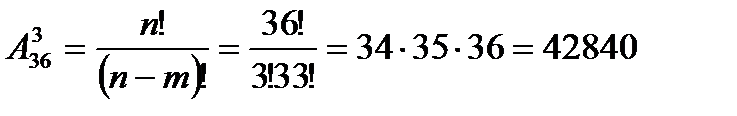
Ответ: 42 840 способами можно раздать 3 карты.
6. В группе учатся 6 студентов и 4 студентки. Наудачу отобраны 7 человек.
Найти вероятность того, что среди отобранных лиц окажутся три девушки.
Решение
Р(А) =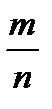 
n – общее число возможных элементарных исходов испытания равно числу способов, которыми можно выбрать 7 человек из 10 человек, учащихся в группе:
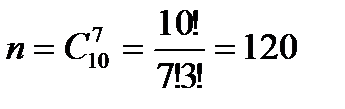
m – число исходов, благоприятных для интересующего нас события: среди 7 человек оказалось 3 девушки. Трех девушек можно выбрать из четырех:
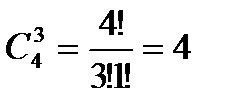способами, при этом остальные 4 человека должны быть юношами и их можно выбрать из 6 студентов
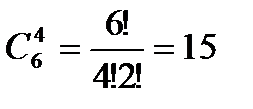способами.
Следовательно, исходя из правила умножения комбинаторики, число благоприятствующих исходов равно:
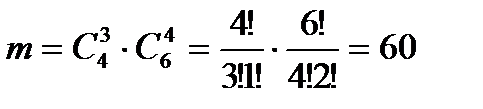
Тогда искомая вероятность:
Р(А) =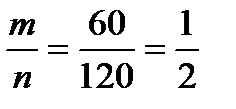 
Ответ: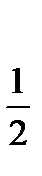 
16
Задачи для самостоятельного решения:
1. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали.
Найти вероятность того, что среди извлечённых деталей:
а) нет брака;
б) нет годных
Ответ: а) р = 0,65 б) р = 0,00005
2. Библиотечка состоит из десяти различных книг, причём пять книг стоят по 4 р. каждая, три книги – по 1 р. И две книги – по 3 р.
Найти вероятность того, что взятые наудачу две книги стоят 5 рублей.
Ответ: р =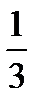 
3. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов.
Найти вероятность того, что среди отобранных студентов 5 отличников.
Ответ: р =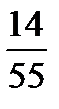 
Вопросы для самопроверки.
1. Какие виды событий вы можете назвать?
2. Что такое испытание и событие?
3. Назовите виды случайных событий.
4. Что такое полная группа событий?
5. Дайте определение вероятности.
6. Перечислите свойства вероятности.
7. Назовите и запишите основные формулы комбинаторики.
8. Приведите примеры:
а) прим. перестановок;
б) прим. размещений;
в) прим. сочетаний.
17
Дата: 2018-11-18, просмотров: 564.
