По предмету «Теория вероятностей и математическая статистика».
09.02.03. «Программирование в компьютерных системах»
Для студентов заочного отделения.
Санкт-Петербург
2018 год
| РАССМОТРЕНЫ: предметной (цикловой) комиссией математики и физики Протокол № ____ от «______» ____________2018 г. Председатель ПЦК Е.В. Кудрявцева ___________________________ подпись | УТВЕРЖДАЮ: Зам. Директора по УМР ____________Е.Г. Конакина «___»______________2018 г. |
| Рекомендованы Методическим советом УПК СПбПУ Протокол №___ от «___» __________2018 г. Старший методист О.М. Симонова ___________________ подпись |
Зам. директора по УМР
Е.Г. Конакина ___________________
подпись
Методические рекомендации по выполнению практических работ и контрольной работы разработаны на основе Федеральных государственных образовательных стандартов (далее – ФГОС) по специальности среднего профессионального образования (далее - СПО) 09.02.03 «Программирование в компьютерных системах» и учебных планов Университетского политехнического колледжа федерального государственного автономного образовательного учреждения высшего образования «Санкт-Петербургский политехнический университет Петра Великого».
Разработчик: Ю. А. Муравьёва, преподаватель УПК СПбПУ
Пояснительная записка.
Методические указания к выполнению внеаудиторной самостоятельной работы студентов по дисциплине «Теория вероятностей и математическая статистика» предназначены для студентов заочного отделения 2-го курса по специальности 09.02.03. «Программирование в компьютерных системах».
Цель методических указаний: оказание помощи студентам в выполнении практических работ и контрольной работы по дисциплине «Теория вероятностей и математическая статистика».
В результате изучения дисциплины студент
Должен знать:
- основы теории вероятностей;
- основы математической статистики.
Должен уметь:
- вычислять вероятность событий с использованием элементов комбинаторики;
- использовать методы математической статистики.
В результате освоения учебной дисциплины у обучающегося формируются общие и профессиональные компетенции:
- ОК 1 – Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
- ОК 2 – Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
- ОК 3 – Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
- ОК 4 – Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
- ОК 5 – Использовать информационно-коммуникационные технологии в профессиональной деятельности.
- ОК 6 – Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
3
- ОК 7 – Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
3
- ОК 8 – Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
- ОК 9 – Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
- ПК 1.1 – Выполнять разработку спецификаций отдельных компонент.
- ПК 1.2 – Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля.
- ПК 2.4 – Реализовывать методы и технологии защиты информации в базах данных.
- ПК 3.4 – Осуществлять разработку тестовых наборов и тестовых сценариев.
Знания по дисциплине приобретаются студентами в процессе проведения занятий и в процессе самоподготовки.
Умения формируются при решении практических работ.
В данном пособии даны рекомендации по оформлению практических работ и контрольной работы, литература для самостоятельного изучения студентами, вопросы для самопроверки, образцы решения задач стандартного вида.
При выполнении практических работ и контрольной работы студент должен руководствоваться следующими указаниями:
1. Контрольная работа и практические работы выполняются в отдельной тетради в клетку, на титульном листе которой должны быть ясно написаны фамилия студента, его инициалы, курс, специальность, e-mail, сотовый телефон, домашний адрес.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4
4. Контрольная работа и практические работы выполняются самостоятельно.
5. В случае незачета по контрольной работе или по практическим работам студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работы на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале. Варианты практических работ и контрольной работы представлены в приложении.
Перед выполнением практических работ и контрольной работы студент должен изучить соответствующие разделы курса “Теория вероятностей и математическая статистика”, используя учебные издания, Интернет-ресурсы, дополнительную литературу и составить конспект. Выполнить практические задания, ответить на вопросы.
Список рекомендуемой литературы приведен в методических указаниях. Студент может использовать также учебники и учебные пособия, не включенные в данный список, если эти пособия содержат соответствующие разделы учебного курса.
Однако, в случае возникновения затруднений при самостоятельном изучении материала, студент может обратиться к преподавателю теории вероятностей и математической статистики для получения устной консультации.
Конспект – это краткое изложение или краткая запись содержания.
Требования к конспекту: системность, логичность изложения, краткость, убедительность и доказательность.
Этапы конспектирования:
1. Прочитайте текст, отметьте в нем непонятные места, новые термины, перечислите основные мысли текста, составьте план.
2. Выясните значение новых непонятных терминов и символов.
3. Вторичное чтение сочетайте с записями основных мыслей. Запись ведите своими словами, не переписывайте текст дословно.
Правила записи текста:
1. Запись должна быть компактной.
5
2. В тексте необходимо применять выделения и разграничения: подчеркивание (для выделения заголовка и подзаголовка, выводов, отделения одной темы от другой, одного вопроса от другого); красную строку для обозначения абзацев и пунктов плана; нумерацию абзацев; выделение с помощью рамки определений, правил, законов, формул и так далее.
3. При записи допускается пользоваться сокращениями.
4. Сформулируйте и запишите вывод.
Цель написания практических работ и контрольной (домашней) работы - оценить освоенные умения и усвоенные знания.
Порядок выполнения самостоятельной работы:
Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надёжности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках.
Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приёмочном контроле качества продукции и для многих других целей.
Событие случайное.
Теория вероятностей не ставит задачу предсказать, произойдёт случайное событие или нет.
Другое дело, если рассматриваются случайные события, которые могут многократно повторяться при одних и тех же условиях. Например, если много раз бросить монету, то можно с небольшой погрешностью предсказать количество выпадений орла или решки. Следовательно, подведём итог:
Испытания и события.
Далее мы не будем говорить: осуществлена совокупность условий, а просто произведено испытание. Поэтому событие – результат испытания.
Пример. а) стрелок стреляет по мишени. Выстрел – это испытание. Попадание в определенную область – событие.
б) в корзине красные и белые шары. Их достают. Извлечение шара – испытание. Появление красных или белых шаров – событие.
7
Виды случайных событий.
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Пример. Брошена монета.
События «появился орел» и «появилась решка» – несовместные.
Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Появление хотя бы одного из событий полной группы есть достоверное событие.
Пример. а) стрелок совершил выстрел по цели. Обязательно произойдёт: либо попадание, либо промах. Эти 2 несовместных событий образуют полную группу.
б) 2 билета «Русского лото». Может произойти только одно из 4-х событий:
* выиграл 1-й билет, не выиграл 2-й;
* не выиграл 1-й, выиграл 2-й;
* выиграли оба билета;
* не выиграл ни один билет.
Эти события образуют полную группу попарно несовместных событий.
Если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. События называют равновозможными, если ни одно из них не является более возможным, чем другое.
Пример. а) Монета – выпадение орла или решки – события равновозможные.
б) игральная кость – появление любого количества очков равно возможно.
Свойства вероятности.
а) Вероятность достоверного события равна 1.
Действительно, каждый элементарный исход является благоприятным для события А, т.е. m = n Р(А) = 1.
б) Вероятность невозможного события равна 0.
Т.е. m = 0 и Р(А) = 0/n = 0.
в) Вероятность случайного события есть положительное число, заключённое между 0 и 1.
0 < m < n 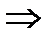 0 <
0 < 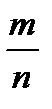 < 1
< 1 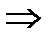 0 < Р(А) < 1
0 < Р(А) < 1
Следовательно, вероятность любого события удовлетворяет следующему неравенству:
| 0 ≤ Р(А) ≤ 1 |
9
Примеры решения задач:
1. Набирая номер телефона, абонент забыл одну цифру и набрал её наудачу.
Найти вероятность того, что набрана нужная цифра.
Решение
Событие А – набрана нужная цифра.
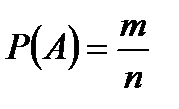 ; n = 10 m = 1 (нужная цифра лишь одна).
; n = 10 m = 1 (нужная цифра лишь одна).
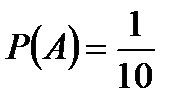 .
.
Ответ: Р(А)=0,1.
2. В ящике 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь.
Найти вероятность того, что извлечённая деталь окажется окрашенной.
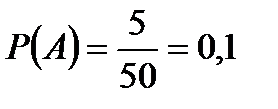 .
.
Ответ: Р(А) = 0,1.
3. Брошена игральная кость.
Найти вероятность того, что выпадет чётное число очков.
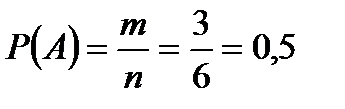
Ответ: Р(А) = 0,5
4. Участники жеребьёвки тянут из ящика жетоны с номерами от 1 до 100.
Найти вероятность того, что номер первого наудачу извлечённого жетона не содержит цифры 5.
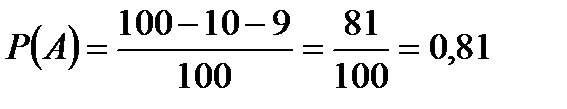
Ответ: р = Р(А)= 0,81.
5. Брошены 2 игральные кости.
Найти вероятность того, что сумма очков на выпавших гранях равна семи.
m=6 (1+6; 2+5; 3+4; 4+3; 5+2; 6+1)
n= 
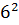 =36 (6 – граней на одной кости; 2 – количество костей).
=36 (6 – граней на одной кости; 2 – количество костей).
10
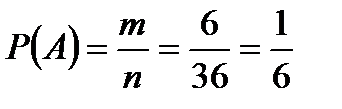
Ответ: р = Р(А)= 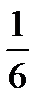
6. Брошены 2 игральные кости.
Найти вероятность того, что сумма очков на выпавших гранях равна пяти, а произведение – четырём.
m=2 (1+4; 4+1)
n= 
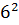 =36 (6 – граней на одной кости; 2 – количество костей).
=36 (6 – граней на одной кости; 2 – количество костей).
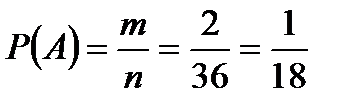
Ответ: р = Р(А)= 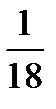
Задачи для самостоятельного решения:
1. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем перемешаны.
Найти вероятность того, что наудачу извлечённый кубик будет иметь сокращённых граней:
| а) одну | б) две | в) три |
Ответ: а) 0,384; б) 0,096; в) 0,008
2. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость.
Найти вероятность того, что вторую наудачу извлечённую кость можно приставить к первой, если первая кость:
а) оказалась дублем;
б) не есть дубль.
Ответ: а) 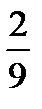 ; б)
; б) 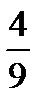 .
.
3. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: О, П, Р, С, Т.
11
Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно прочесть слово «СПОРТ».
Ответ: р = 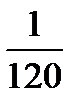
4. На каждой из шести одинаковых карточек напечатана одна из следующих букв: А, Т, М, Р, С, О. Карточки перемешаны.
Найти вероятность того, что на четырёх, вынутых по одной и расположенных «в одну линию» карточках можно прочесть слово «ТРОС».
Ответ: р = 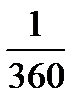
Комбинаторные формулы.
При подсчёте вероятностей большую пользу оказывают формулы комбинаторики:
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества.
Перестановки – комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.
Число возможных перестановок:
Рn = n!
где n! = 1∙2∙3∙. . . ∙n.
Пример. Даны цифры 1, 2, 3. Сколько трехзначных чисел можно составить из них, если каждая цифра входит в изображение числа 1 раз?
Р3 = 3n! = 1∙2∙3 = 6.
Размещения – комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.
Число всех возможных размещений:
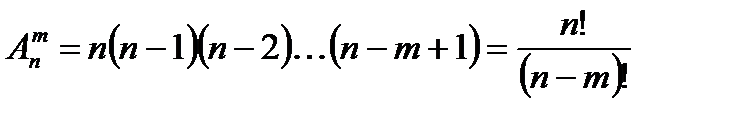
Пример. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
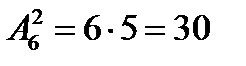
12
Сочетания – комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.
Число сочетаний: 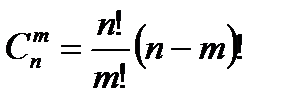
Пример. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Искомое число: 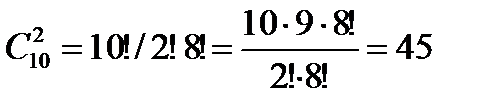 .
.
Числа размещений, перестановок и сочетаний связаны равенством:
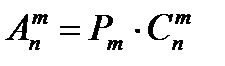
При решении задач комбинаторики существуют следующие правила:
Правило суммы:
Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В – n способами, то выбрать либо А, либо В можно m + n способами.
Правило произведения:
Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.
Примеры решения задач:
1. В ящике содержится 10 одинаковых деталей, помеченных номерами от 1 до 10. Наудачу извлечено 6 деталей.
Найти вероятность того, что среди извлечённых деталей окажется деталь № 1.
Решение
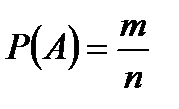
n – общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из десяти:
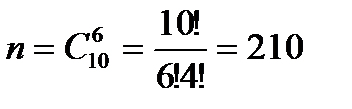
m – число исходов, благоприятных для интересующего нас события: среди отобранных шести деталей есть деталь № 1, и, следовательно, остальные 5
13
деталей имеют другие номера. Число таких исходов равно числу способов, которыми можно отобрать 5 деталей из оставшихся девяти:
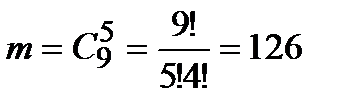
Тогда искомая вероятность:
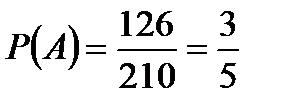 ;
;
Ответ: 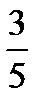
2. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу вынимает три детали.
Найти вероятность того, что извлечённые детали окажутся окрашенными.
Решение
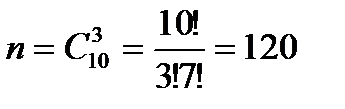
способами можно вынуть три окрашенные детали из десяти.
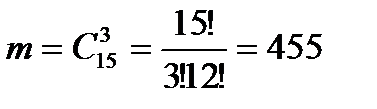
способами можно вынуть три неокрашенные детали из пятнадцати.
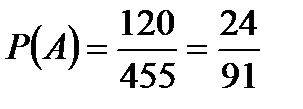
Ответ: р = 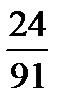
3. Набирая номер телефона, абонент забыл последние три цифры, и, помня, что эти цифры различны, набрал их наудачу.
Найти вероятность того, что набраны нужные цифры.
Решение
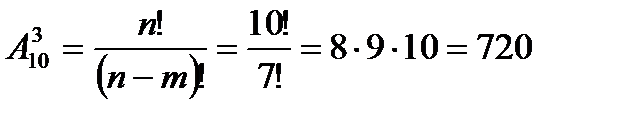
р = 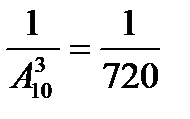
Ответ: р = 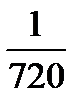
14
4. У Васи живут четыре кота.
а) сколькими способами можно рассадить котов по углам комнаты?
Решение
В задаче речь идёт о разных объектах! Наказанию подвергаются сразу все коты, плюс важно их расположение, поэтому здесь имеют место перестановки.
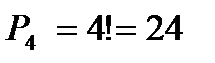
Ответ: 24 способами можно рассадить котов по углам комнаты.
б) сколькими способами можно отпустить гулять котов?
Решение
Предполагается, что коты ходят гулять только через дверь, при этом вопрос подразумевает безразличие по поводу количества животных – на прогулку могут выйти 1, 2, 3 или 4 кота.
Составляем все возможные сочетания:
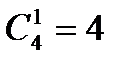 способами можно отпустить гулять одного кота (любого из четырёх).
способами можно отпустить гулять одного кота (любого из четырёх).
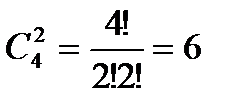 способами можно отпустить гулять двух котов.
способами можно отпустить гулять двух котов.
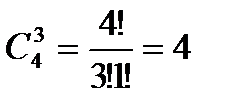 способами можно отпустить гулять трех котов (какой-то один из четырех сидит дома.
способами можно отпустить гулять трех котов (какой-то один из четырех сидит дома.
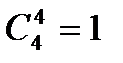 способом можно выпустить всех котов.
способом можно выпустить всех котов.
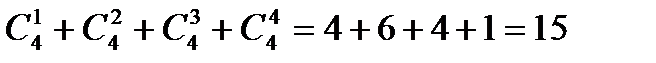
Ответ: 15 способами можно отпустить гулять котов.
в) сколькими способами Вася может взять на руки двух котов (одного – на левую, другого на правую)?
Решение
Ситуация предполагает не только выбор двух котов, но и их размещение по рукам:
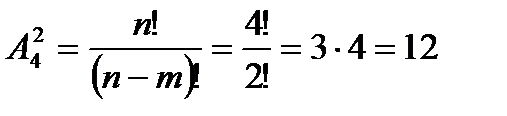
Ответ: 15 способами можно взять на руки двух котов.
5. Боря, Дима и Володя сели играть в «очко». Сколькими способами им можно сдать по одной карте из колоды в 36 карт?
15
Решение
Здесь важно не только то, какие 3 карты будут извлечены из колоды, но и то, как они будут распределены между игроками.
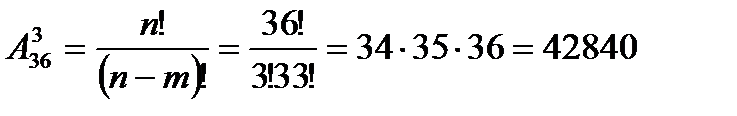
Ответ: 42 840 способами можно раздать 3 карты.
6. В группе учатся 6 студентов и 4 студентки. Наудачу отобраны 7 человек.
Найти вероятность того, что среди отобранных лиц окажутся три девушки.
Решение
Р(А) = 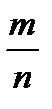
n – общее число возможных элементарных исходов испытания равно числу способов, которыми можно выбрать 7 человек из 10 человек, учащихся в группе:
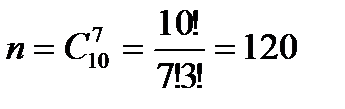
m – число исходов, благоприятных для интересующего нас события: среди 7 человек оказалось 3 девушки. Трех девушек можно выбрать из четырех:
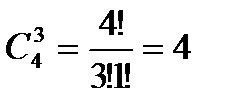 способами, при этом остальные 4 человека должны быть юношами и их можно выбрать из 6 студентов
способами, при этом остальные 4 человека должны быть юношами и их можно выбрать из 6 студентов
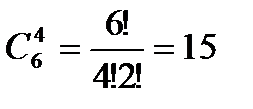 способами.
способами.
Следовательно, исходя из правила умножения комбинаторики, число благоприятствующих исходов равно:
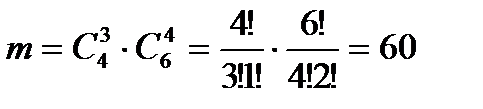
Тогда искомая вероятность:
Р(А) = 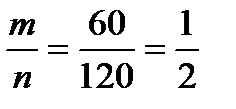
Ответ: 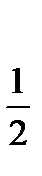
16
Задачи для самостоятельного решения:
1. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали.
Найти вероятность того, что среди извлечённых деталей:
а) нет брака;
б) нет годных
Ответ: а) р = 0,65 б) р = 0,00005
2. Библиотечка состоит из десяти различных книг, причём пять книг стоят по 4 р. каждая, три книги – по 1 р. И две книги – по 3 р.
Найти вероятность того, что взятые наудачу две книги стоят 5 рублей.
Ответ: р = 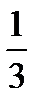
3. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов.
Найти вероятность того, что среди отобранных студентов 5 отличников.
Ответ: р = 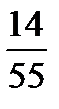
Вопросы для самопроверки.
1. Какие виды событий вы можете назвать?
2. Что такое испытание и событие?
3. Назовите виды случайных событий.
4. Что такое полная группа событий?
5. Дайте определение вероятности.
6. Перечислите свойства вероятности.
7. Назовите и запишите основные формулы комбинаторики.
8. Приведите примеры:
а) прим. перестановок;
б) прим. размещений;
в) прим. сочетаний.
17
Формула полной вероятности.
Следствие.
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р(А1 + А2 + А3 + . . . + Аn) = Р(А1) + Р(А2) + Р(А3) + . . . + Р(Аn) .
Пример. В корзине 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Цветные шары – либо красный, либо синий.
Красный: Р(А) = 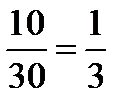 .
.
Синий: Р(В) = 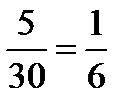 .
.
18
События А и В – несовместны, поэтому теорема применима
Р(А + В) = Р(А) + Р(В) = 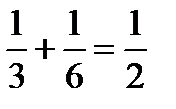 .
.
Ответ: 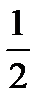
Теорема. Сумма вероятностей событий А1 , А2 , ... Аn, образующих полную группу, равна 1: Р(А1) + Р(А2) + . . . + Р(Аn) = 1.
Доказательство.
Т.к. появление одного из событий полной группы достоверно, а вероятность достоверного события равна 1, то:
Р(А1) + Р(А2) + . . . + Р(Аn) = 1. (1)
Любые два события полной группы несовместны, поэтому можно применить теорему сложения:
Р(А1 + А2 + . . . + Аn) = Р(А1) + Р(А2) + . . . + Р(Аn) . (2)
Сравнивая теперь (1) и (2), получаем: Р(А1) + Р(А2) + . . . + Р(Аn) = 1.
Пример. Фирма получает постоянно пакеты с документами из своих филиалов, расположенных в городах А, В и С.
Вероятность получения пакета из А = 0,7; вероятность получения пакета из В = 0,2. Найти вероятность получения пакета из С.
Решение.
События «получение пакетов» образуют полную группу, поэтому 0,7 + 0,2 + Р(С) = 1. Отсюда: Р(С) = 0,1.
Ответ: Р(С)=0,1.
Противоположные события
Противоположными называют два единственно возможных события, образующих полную группу. Если событие обозначить А, то противоположное ему – 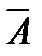 .
.
Пример. 1. Попадание и промах при выстреле по цели – противоположные события.
2. Извлечение из ящика с деталями стандартной или нестандартной детали – событие противоположные.
19
Теорема. Сумма вероятностей противоположных событий равна 1. Р(А) + Р( 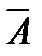 ) = 1 или p + q = 1.
) = 1 или p + q = 1.
Доказательство.
Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу равна 1.
Пример. Вероятность того, что день будет дождливым равна 0,7.
Найти вероятность того, что день будет ясным.
Решение.
События противоположные, поэтому: q = 1 – p = 0,3.
Ответ: q=0,3.
Умножение вероятностей.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.
Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годная и окрашенная.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
Например, если А, В, С – появление герба соответствует в 1, 2, 3 испытаниях, то АВС – выпадение герба во всех трех испытаниях.
Введём понятие условной вероятности.
До сих пор мы говорили о безусловной вероятности: вероятности случайного события, которое может произойти, а может не произойти при совокупных определенных условий.
Если кроме этой совокупности условий налагаются дополнительные условия, то вероятность события называют условной.
Например, вычисляют вероятность события В при дополнительном условии, что событие А уже произошло.
Пример. В урне 3 белых и три черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно.
Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечён черный шар (событие А).
20
Решение.
После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность:
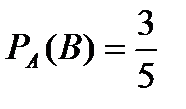
Этот же результат можно получить по формуле:
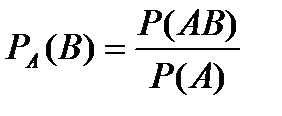 (Р(А) > 0)
(Р(А) > 0)
Действительно, вероятность появления белого шара при первом испытании:
Р(А)= 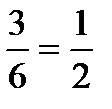
Найдем вероятность Р(АВ) того, что в первом испытании появится черный шар, а во втором белый.
Общее число исходов – совместного появления двух шаров, безразлично какого цвета, равно числу размещений 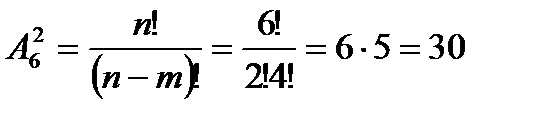
Из этого числа исходов событию АВ благоприятствуют 3∙3=9 исходов. Следовательно, Р(АВ)= 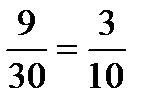
Искомая условная вероятность 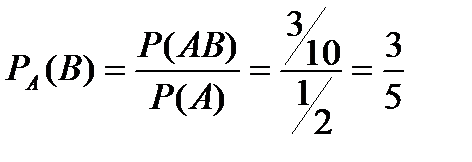
Как видим, получен прежний результат.
Рассмотрим непосредственно теорему умножения вероятностей.
Пусть даны два события А и В, и вероятности Р(А) и Р(В) – известны.
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ) = Р(А) · РА(В).
Следствие.
Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причём вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
Р(А1 А2 А3 . . . Аn) = Р(А1) Р А1 (А2) Р А1А2 (А3) . . . + Р А1А2…Аn-1 (Аn) .
21
Пример. У сборщика имеется 3 конусных и 7 эллиптических валов. Он взял один вал, затем – второй.
Найти вероятность того, что первый из взятых валов – конусный, а второй – эллиптический.
Решение.
Вероятность, что вал конусный 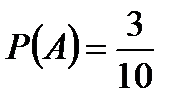 .
.
Вероятность, что второй вал – эллиптический 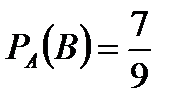 .
.
Искомая вероятность: 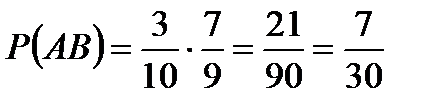 .
.
Для независимых событий теорема умножения имеет вид:
Р(АВ) = Р(А) · Р(В).
Повторение испытаний.
1. Формула Бернулли.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся, что вероятность события А в каждом испытании одна и та же и равна р. Следовательно, вероятность ненаступления события постоянна и равна q.
q = 1 – p
Поставим перед собой задачу вычислить вероятность того, что при n испытаниях событие А осуществится k раз и не осуществится n – k раз.
Искомую вероятность обозначим Рn(k). Например, Р5(3) – событие в 5 испытаниях появляется 3 раза и не появится 2 раза.
Поставленную задачу можно решить с помощью формулы Бернулли.
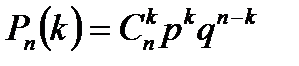
|
Пример. Вероятность того, что расход электроэнергии в продолжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение
р =0,75, вероятность перерасхода q = 1 – 0,75 = 0,25. Р6(4) = 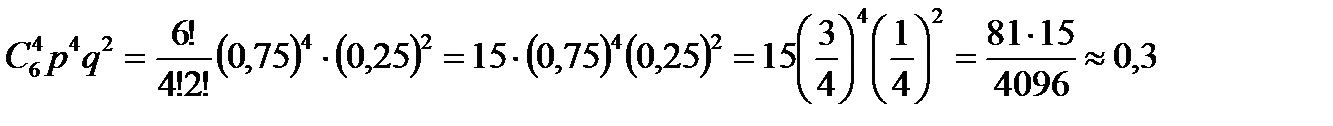
2. Локальная теорема Лапласа.
Пользоваться формулой Бернулли при больших значениях n затруднено, т.к. надо производить действия над громадными числами. Поэтому есть другая формула, которая позволяет найти вероятность появления события k раз в n испытаниях, если число испытаний велико.
Это формула Лапласа.
Теорема. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рn(k) того, что событие А появится в n испытаниях ровно k раз, равна:
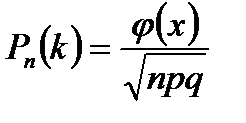 при х =
при х = 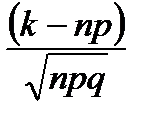
28
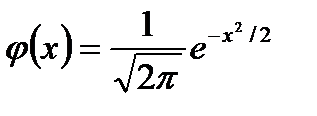
|
Имеются таблицы, в которых находятся значения функции φ(х), соответствующие положительным значениям аргумента. Для отрицательных значений пользуются теми же таблицами, т.к. функция φ(х) – чётная, т.е. φ(–х) = φ(х).
Пример 1. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение.
n = 400
k = 80
p = 0,2
q = 0,8
По формуле Лапласа:
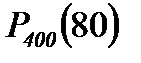 =
= 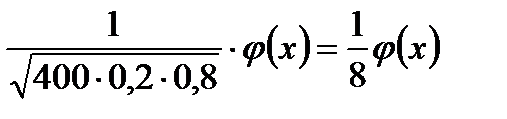
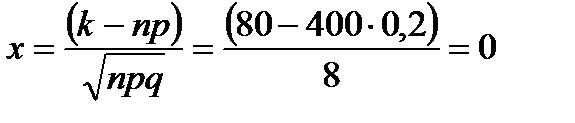
φ(0) = 0,3989
Искомая вероятность: 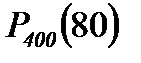 =
= 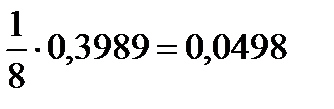 .
.
Если считать по формулам Бернулли, то 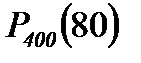 = 0,0498.
= 0,0498.
Пример 2. Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.
Решение.
n = 10
k = 8
p = 0,75
q = 0,25
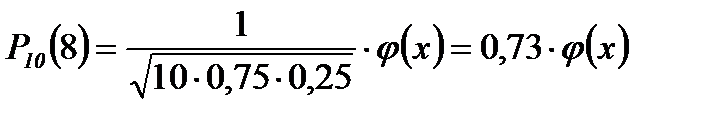
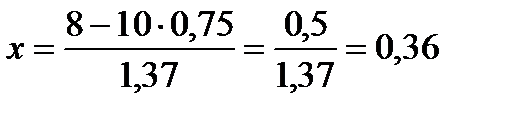
29
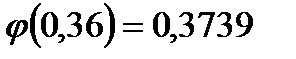
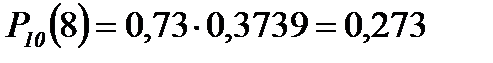
Если считать по формуле Бернулли, то получим: 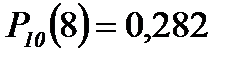 . Это ближе к истине, т.к. формула Лапласа даёт хорошие результаты при достаточно больших n.
. Это ближе к истине, т.к. формула Лапласа даёт хорошие результаты при достаточно больших n.
3. Интегральная теорема Лапласа.
Опять предположим, что проводится n испытаний, в каждом из которых вероятность появления события А постоянна и 0 < р < 1.
Как вычислить вероятность того, что событие А появится в n испытаниях не менее k1 и не более k2 раз (т.е. от k1 до k2 раз). На этот вопрос даёт ответ интегральная теорема Лапласа:
Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рn(k1 k2) того, что событие А появится в n испытаниях от k1 до k2 раз, равна:
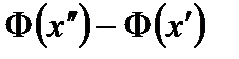 ,
,
где 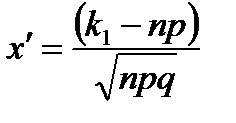 и
и 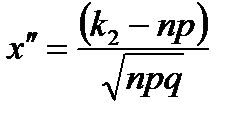 .
.
Функция 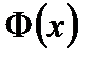 называется функцией Лапласа.
называется функцией Лапласа.
Есть таблицы, где вычислены и приводятся её значения, для положительных значений аргумента. Для отрицательных значений пользуются той же таблицей, только надо помнить, что 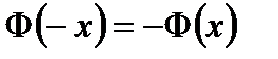 при
при 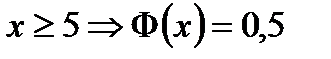 .
.
Пример. Вероятность того, что деталь не прошла проверку р = 0,2.
Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение.
p = 0,2
q = 0,8
n = 400
k1 = 70
k2 = 100
P400(70, 100) = 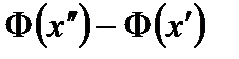
30
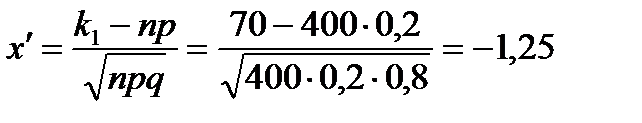
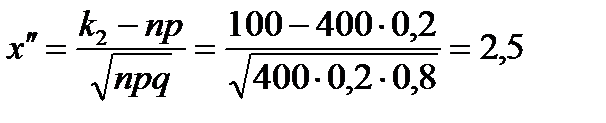
Ф(–1,25) = –0,3944
Ф(2,5) = 0,4938
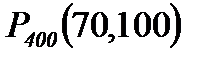 = 0,4938 + 0,3944 = 0,8882.
= 0,4938 + 0,3944 = 0,8882.
Вопросы для самопроверки:
1. Формула Бернулли. В каком случае её применяют?
2. Локальная теорема Лапласа. Отличие от формулы Бернулли. Особенности функции 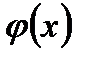 .
.
3. Интегральная теорема Лапласа. Особенности функции 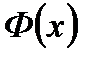 .
.
После изучения теории и решения задач из раздела 1, можно выполнять практическую работу №1.
31
Распределение Пуассона.
Если число испытаний n велико, то пользуются формулой Лапласа. Однако, эта формула становится непригодной, если вероятность события мала 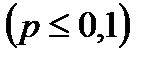 . В этих случаях (n – велико, р – мало) при бегают к асимптотической формуле Пуассона.
. В этих случаях (n – велико, р – мало) при бегают к асимптотической формуле Пуассона.
Пусть нам надо найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз.
Сделаем допущение: произведение np сохраняет постоянное значение, а именно np = 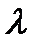 . Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях n, остается неизвестным.
. Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях n, остается неизвестным.
Воспользуемся формулой Бернулли:
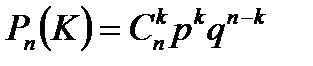 .
.
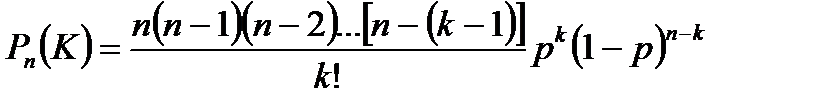
Т.к. np = 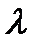 , то p =
, то p = 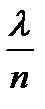 , следовательно
, следовательно
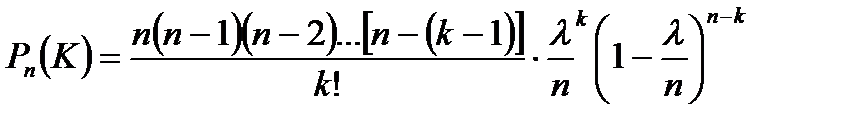
Т.к. n имеет очень большое значение, вместо Рn(k) найдём 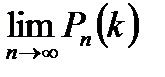 . При этом мы найдём приближённое значение отыскиваемой вероятности, т.к. n хотя и велико, но конечно. Т.к. np = const, то при
. При этом мы найдём приближённое значение отыскиваемой вероятности, т.к. n хотя и велико, но конечно. Т.к. np = const, то при 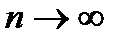 ,
, 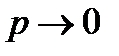 .
.
35
Следовательно, 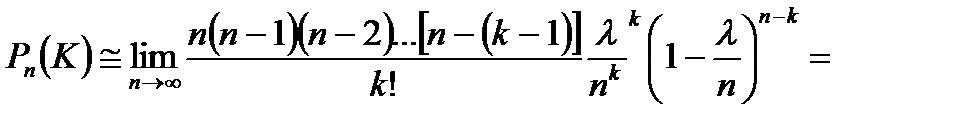
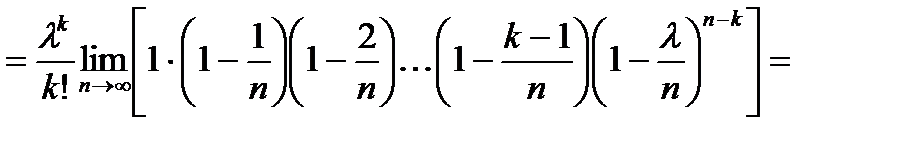
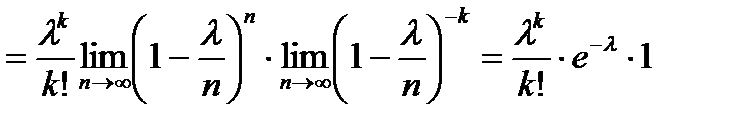
Т.о.
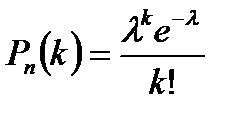
|
где е = 2,71828… – основание натурального ln.
– закон распределения Пуассона.
Pn(k)
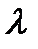 k
k
Пример. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделий повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделий.
Решение.
n = 5000
k = 3
p = 0,0002
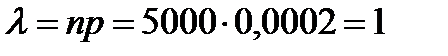 .
.
По формуле Пуассона: Р5000(3) = 13·е-1/3! = 0,06
Ответ: 0,06
36
Примеры решения задач:
1. В магазине имеется 15 автомобилей определённой марки. Среди них 7 чёрного цвета, 6 серого и 2 белого. Представители фирмы обратились в магазин с предложением о продаже им 3 автомобилей этой марки, безразлично какого цвета. Составьте ряд распределения числа проданных автомобилей чёрного цвета при условии, что автомобили отбирались случайно.
Решение
Введём дискретную случайную величину Х = (число проданных автомобилей чёрного цвета). Х может принимать значения 0, 1, 2 и 3. Найдём соответствующие вероятности по классическому определению вероятности.
Всего способов выбрать 3 любых автомобиля из 15 будет:
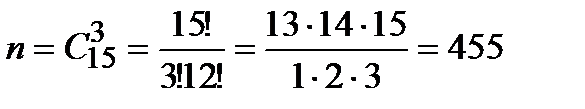 .
.
Х = 0, если все автомобили не чёрные, таких было 8 штук, поэтому 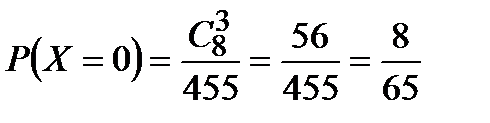 .
.
Х = 1, если один автомобиль чёрный, (выбираем из 7) и ещё два не чёрные (выбираем из 8 остальных), поэтому 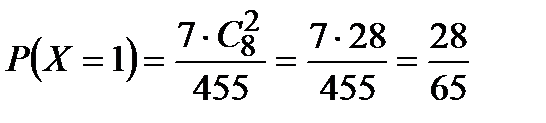 .
.
Х = 2, если два автомобиля чёрные, (выбираем из 7) и ещё один не чёрный (выбираем из 8 остальных), поэтому 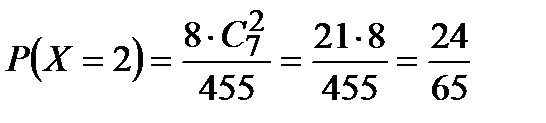 .
.
Х = 3, если все автомобили чёрные, вероятность 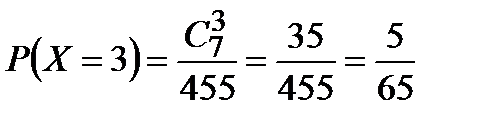 .
.
Ряд распределения случайной величины Х :
| хi | 0 | 1 | 2 | 3 |
| рi | 8/65 | 28/65 | 24/65 | 5/65 |
Сумма вероятностей равна 1, распределение найдено верно.
2. В городе 4 коммерческих банка. У каждого риск банкротства в течение года составляет 20%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года.
37
Решение
Пусть Х – дискретная случайная величина (ДСВ), равная числу банков, которые могут обанкротиться в течение следующего года. Она может принимать значения 0, 1, 2, 3, 4. ДСВ Х распределена по биноминальному закону с параметрами n=4, р=20%=0,2, поэтому найдём соответствующие вероятности по формуле Бернулли:
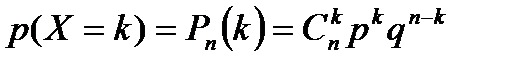 , где q = 1 – p
, где q = 1 – p
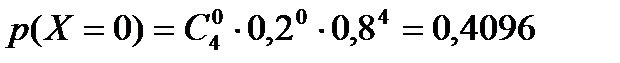
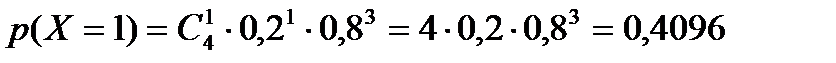
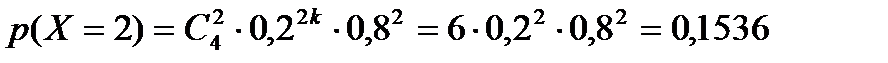
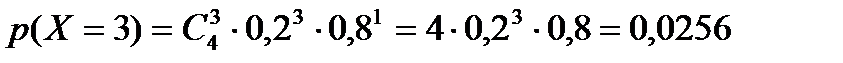
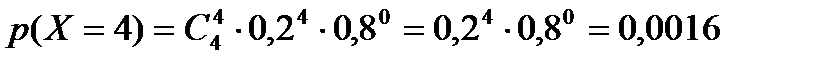
Таким образом, закон распределения случайной величины Х имеет вид:
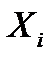
| 0 | 1 | 2 | 3 | 4 |

| 0,4096 | 0,4096 | 0,1536 | 0,0256 | 0,0016 |
0,4096+0,4096+0,1536+0,0256+0,0016=1
Следовательно, распределение найдено верно.
Вопросы для самопроверки:
1. Что такое случайная величина?
2. Определение дискретной случайной величины.
3. Что такое закон распределения дискретной случайной величины.
4. Что такое биноминальное распределение? В каком случае оно применяется? Формула.
5. В каких случаях применяют распределение Пуассона? Формула.
Свойства.
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: М(С) = С.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = СМ(Х).
40
Приведём 3 замечания:
1. Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае они зависимы.
2. Произведение независимых случайных величин Х и У определим как случайную величину ХУ, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение У. Вероятности возможных значений ХУ равны произведениям вероятностей возможных значений сомножителей.
3. Сумму случайных величин Х и У определим как случайную величину Х + У, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением У. Вероятности возможных значений Х + У равны произведениям вероятностей слагаемых.
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: М(ХУ) = М(Х)М(У).
Доказательство:
Пусть независимые случайные величины Х и У заданы своими законами распределения вероятностей:
| Х | x1 x2 | У | у1 у2 | |
| р | р1 р2 | G | g1 g2 |
Составим все значения, которые может принимать случайная величина ХУ. Для этого перемножим все возможные значения Х на каждое возможное значение У. Учитывая замечание 2, получим:
| ХУ | x1 у1 | x2 у1 | x1 у2 | x2 у2 |
| р | р1 g1 | р2 g1 | р1 g2 | р2 g2 |
Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:
41
М(ХУ) = x1 у1· р1 g1 + x2 у1· р2 g1 + x1 у2· р1 g2 + x2 у2· р2 g2
или
М(ХУ) = у1g1(x1р1 + x2 р2) + у2g2 (x1р1 + x2 р2) = М(Х)М(У).
Следствие : Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
М( XYZ ) = M(X)M(Y)M(Z).
Пример. Независимые случайные величины Х и У заданы следующими законами распределения:
| Х | 5 | 2 | 4 | У | 7 | 9 | |
| р | 0,6 | 0,1 | 0,3 | g | 0,8 | 0,2 |
Найти математическое ожидание ХУ.
Решение.
Найдём математические ожидания каждой из данных величин:
М(Х) = 5·0,6 + 2·0,1 + 4·0,3 = 4,4
М(У) = 7·0,8 + 9·0,2 = 7,4
Тогда М(ХУ) = 4,4·7,4 = 32,56.
Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: М(Х + У) = М(Х) + М(У) .
Следствие: Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
Пример. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.
Решение.
Обозначим число очков, которое может выпасть на первой кости, через Х, на второй – У. Возможные значения этих величин одинаковы и равны 1, 2, 3, 4, 5, 6, причём вероятность каждого из них равна 1/6.
Найдём М числа очков, которые могут выпасть на первой кости:
42
М(Х) = 1·1/6 + 2·1/6 + 3·1/6 + 4·1/6 + 5·1/6 + 6·1/6 = 7/2
М(У) = 7/2 аналогично.
Искомое М: М(Х + У) = 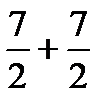 = 7.
= 7.
Для биномиального распределения:
Теорема: Математическое ожидание М(Х) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: М(Х) = np
Пример. Вероятность попадания в цель при стрельбе из орудия р = 0,6. Найти М общего числа попаданий, если будет произведено 10 выстрелов.
М(Х) = np = 10·0,6 = 6 (попаданий).
Свойства дисперсии.
Свойство 1. Дисперсия постоянной величины С = 0.
D(C) = 0.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D(C Х) = С2D(Х).
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D(Х + У) = D(Х) + D(У) .
Следствие : Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.
Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D(Х – У) = D(Х) + D(У) .
Пример. Дисперсия случайной величины Х равна 5. Найти дисперсию следующих величин: а) х – 1; б) –2х; в) 3х + 6.
а) D (х – 1) = D (Х) + D (1) = 5;
б) D (–2х) = (–2)2·5 = 20;
в) D (3х + 6) = (3)2·5 = 45.
44
Для биномиального распределения:
Теорема. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:
D(Х) = npq.
Пример. Производится 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины Х – числа появлений события в этих испытаниях.
Решение.
q = 1 – 0,6 = 0,4
D(Х) = 10·0,4·0,6 = 2,4.
Примеры решения задач:
1. На пути движения автомашины 4 светофора, каждый из которых запрещает дальнейшее движение автомашины с вероятностью 0,5. Найти ряд распределения числа светофоров, пройденных машиной до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины?
Решение
Пусть Х – дискретная случайная величина, равная числу светофоров, пройденных автомобилем до первой остановки, она может принимать значения 0, 1, 2, 3, 4.
Случайная величина Х принимает значение равное 0, если автомобиль попал на запрещающий сигнал на первом же светофоре, вероятность этого Р(Х = 0) = 0,5.
Случайная величина Х принимает значение равное 1, если автомобиль проехал на первом светофоре и попал на запрещающий сигнал на втором светофоре, вероятность этого
Р(Х = 1) = 0,5·0,5 = 0,25.
Случайная величина Х принимает значение равное 2, если автомобиль проехал на первом и втором светофоре и попал на запрещающий сигнал на третьем светофоре, вероятность этого Р(Х = 2) = 0,5·0,5·0,5 = 0,125.
Случайная величина Х принимает значение равное 3, если автомобиль проехал на первом, втором и третьем светофоре и попал на запрещающий сигнал на четвертом светофоре, вероятность этого Р(Х = 3) = 0,5 · 0,5 · 0,5 · 0,5 = 0,54 = 0,0625.
Случайная величина Х принимает значение равное 4 если автомобиль проехал на всех 4 светофорах, вероятность этого Р(X = 4) = 0,54 = 0,0625.
45
Таким образом, закон распределения случайной величины Х имеет вид:
| хi | 0 | 1 | 2 | 3 | 4 |
| рi | 0,5 | 0,25 | 0,125 | 0,0625 | 0,0625 |
Расчеты произведены правильно, так как сумма 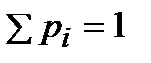 .
.
Математическое ожидание:
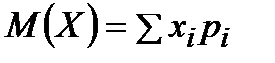 = 0·0,5 + 1·0,25 + 2·0,125 + 3·0,0625 + 4·0,0625 = 0,9375.
= 0·0,5 + 1·0,25 + 2·0,125 + 3·0,0625 + 4·0,0625 = 0,9375.
Дисперсия:
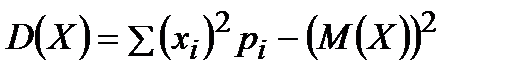 =
=
= 02·0,5 + 12·0,25 + 22·0,125 + 32·0,0625 + 42·0,0625 – 0,93752 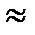 1,434.
1,434.
2. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырёх выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Найти дисперсию этой случайной величины.
Решение
Введём дискретную случайную величину Х – (число промахов) Х – может принимать значения 0, 1, 2, 3, 4.
Найдём соответствующие вероятности.
Х = 0, если охотник попал в дичь при первом выстреле, поэтому Р(Х = 0) = 0,7.
Х = 1, если охотник не попал в дичь при первом выстреле и попал в дичь при втором выстреле, поэтому Р(Х = 1) = 0,3·0,7 = 0,21.
Х = 2, если охотник не попал в дичь при первом выстреле и втором выстреле, и попал в дичь при третьем выстреле, поэтому Р(Х = 2) = 0,3·0,3·0,7 = 0,063.
Х = 3, если охотник не попал в дичь при первом, втором и третьем выстрелах, и попал в дичь при четвёртом выстреле, поэтому Р(Х = 3) = 0,3·0,3·0,3·0,7 = 0,0189.
Х = 4, если охотник не попал в дичь при первом, втором, третьем и четвёртом выстрелах, поэтому Р(Х = 4) = 0,3·0,3·0,3·0,3·0,7 = 0,0081.
Закон распределения случайной величины Х имеет вид:
| хi | 0 | 1 | 2 | 3 | 4 |
| рi | 0,7 | 0,21 | 0,063 | 0,0189 | 0,0081 |
46
Найдём числовые характеристики дискретной случайной величины Х:
Математическое ожидание:
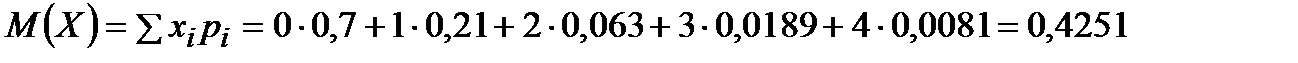
Дисперсия:
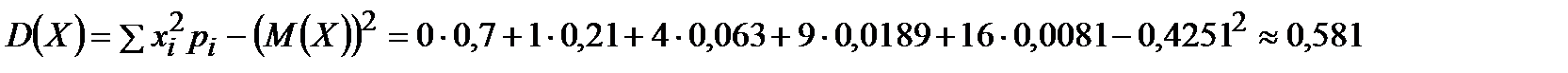
Вопросы для самопроверки:
1. Что такое математическое ожидание?
2. Чему равно математическое ожидание числа появления события в одном испытании?
3. Вероятностный смысл математического ожидания.
4. Свойства математического ожидания (4 свойства).
5. Что такое независимые случайные величины?
6. Что понимают под произведением независимых случайных величин? Чему равны вероятности значений ХУ?
7. Что такое сумма независимых случайных величин?
8. Математическое ожидание числа появления события в n независимых испытаниях?
9. Отклонение случайной величины от её математического ожидания – что это?
10. Что характеризует дисперсия?
11. Свойства дисперсии (4 свойства).
12. Дисперсные числа появления события в n независимых испытаниях.
После изучения теории и решения задач из раздела 2, можно выполнять практическую работу №2.
После выполнения и защиты практических работ №1 и №2, можно выполнять контрольную работу.
47
Приложение.
Студент выполняет тот вариант, который совпадает с его номером в журнале.
| номер в журнале | номер варианта |
| 1, 11, 21, 31 | 1 |
| 2, 12, 22, 32 | 2 |
| 3, 13, 23, 33 | 3 |
| 4, 14, 24, 34 | 4 |
| 5, 15, 25, 35 | 5 |
| 6, 16, 26 | 6 |
| 7, 17, 27 | 7 |
| 8, 18, 28 | 8 |
| 9, 19, 29 | 9 |
| 10, 20, 30 | 10 |
Практическая работа № 1.
Задание 1.
Рассчитать вероятность события с помощью формулы классического определения вероятности: 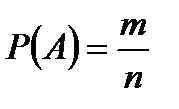 .
.
56
Задания 2, 3.
Рассчитать вероятность события, используя формулы комбинаторики и основные теоремы теории вероятностей.
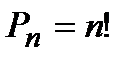 – перестановки,
– перестановки,
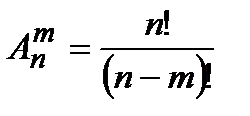 – размещения,
– размещения,
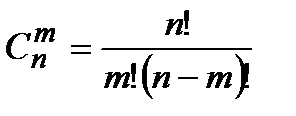 – сочетания.
– сочетания.
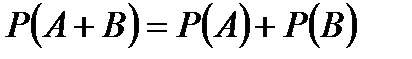 – формула сложения вероятностей,
– формула сложения вероятностей,
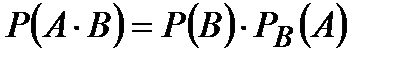 – формула умножения вероятностей,
– формула умножения вероятностей,
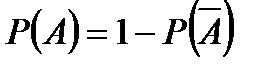 – вероятность события, рассчитанная через вероятность противоположного события.
– вероятность события, рассчитанная через вероятность противоположного события.
Вариант 1
Задача 1.
Бросают две монеты. Найти вероятность того, что:
а) на обеих монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) меньше, чем 2 белых шара;
в) хотя бы один белый шар.
Задача 3.
Вероятность того, что событие появится хотя бы один раз в трех независимых испытаниях, равна 0,936.
Найти вероятность появления события в одном испытании (предполагается, что во всех испытаниях вероятность появления события одна и та же).
Вариант 2
Задача 1.
Бросают три монеты. Найти вероятность того, что:
а) на всех монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
57
а) 3 белых шара;
б) меньше, чем 3 белых шара;
в) хотя бы один белый шар.
Задача 3.
В типографии имеется 4 печатные машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9.
Найти вероятность того, что в данный момент работает хотя бы одна машина.
Вариант 3
Задача 1.
Бросают четыре монеты. Найти вероятность того, что:
а) на всех монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 6 черных и 5 белых шаров. Случайным образом вынимают 4 шара.
Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) меньше, чем 2 белых шара;
в) хотя бы один белый шар.
Задача 3.
У сборщика имеется 16 деталей, изготовленных заводом № 1, и 4 детали, изготовленные заводом № 2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом № 1.
Вариант 4
Задача 1.
Бросают две игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:
а) только чётные;
б) одно чётное, другое нечётное;
в) сумма которых делится на три.
Задача 2.
В урне содержатся 7 чёрных и 4 белых шара. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) меньше, чем 2 белых шара;
в) хотя бы один белый шар.
Задача 3.
Брошена монета и игральная кость. Найти вероятность совмещения событий «появился орел», «появилось 6 очков».
58
Вариант 5
Задача 1.
Бросают две игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:
а) только нечётные;
б) одно нечётное, другое чётное;
в) сумма которых делится на четыре.
Задача 2.
В урне содержатся 8 чёрных и 6 белых шаров. Случайным образом вынимают 5 шаров.
Найти вероятность того, что среди них имеется:
а) три белых шара
б) меньше, чем 3 белых шара
в) хотя бы один белый шар.
Задача 3.
Вероятность того, что при одном выстреле стрелок выбьет 10 очков, равна 0,1; вероятность выбить 9 очков 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.
Вариант 6
Задача 1.
Бросают 3 игральные кости. Найти вероятность того, что на верхних гранях появятся
следующие числа очков:
а) только чётные;
б) которые все одинаковы;
в) хотя бы на одной из костей появится 6 очков.
Задача 2.
В урне содержатся 6 чёрных и 7 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) три белых шара;
б) меньше, чем 3 белых шара;
в) хотя бы один белый шар.
Задача 3.
События А, В, С, D образуют полную группу. Вероятности событий таковы: Р(А) = 0,1; Р(В) = 0,4; Р(С) = 0,3. Чему равна вероятность события D?
59
Вариант 7
Задача 1.
Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится:
а) только нечетные;
б) которые все одинаковы;
в) хотя бы на одной из костей появится 4 очка.
Задача 2.
В урне содержится 8 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 3 белых шара;
б) меньше, чем 3 белых шара;
в) хотя бы один белый шар.
Задача 3.
Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в 1-ю область равна 0,45, во 2-ю – 0,35. Найти вероятность того, что стрелок при одном выстреле попадает либо в первую, либо во вторую область.
Вариант 8
Задача 1.
Бросают три монеты. Найти вероятность того, что:
а) на всех монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 8 белых и 6 черных шаров. Случайным образом вынимают 5 шаров.
Найти вероятность того, что среди них имеется:
а) 2 белых шара
б) меньше, чем 2 белых шара
в) хотя бы один белый шар
Задача 3.
В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А) при втором – чёрный (событие В) и при третьем – синий (событие С).
60
Вариант 9
Задача 1.
Бросают две монеты. Найти вероятность того, что:
а) на обеих монетах появится орел;
б) хотя бы на одной монете появится орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 7 белых и 5 черных шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
а) 3 белых шара
б) меньше, чем 3 белых шара
в) хотя бы один белый шар
Задача 3.
При стрельбе из винтовки относительная частота попадания в цель, оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов.
Вариант 10
Задача 1.
Брошены две монеты. Найти вероятность того, что:
а) на обеих монетах появился орел;
б) хотя бы на одной монете появился орел;
в) ни на одной монете не появится орел.
Задача 2.
В урне содержится 5 белых и 6 черных шаров. Случайным образом вынимают 3 шара. Найти вероятность того, что среди них имеется:
а) 2 белых шара
б) меньше, чем 2 белых шара
в) хотя бы один белый шар
Задача 3.
В студии телевидения 3 камеры. Для каждой вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера.
61
Практическая работа № 2.
Задание 1.
Рассчитать математическое ожидание суммы и произведения двух дискретных случайных величин двумя
способами: составив общий закон распределения и по формуле математического ожидания
M(x) = р1х1 + р2х2 + р3х3 + … + рnхn
где х1, х2 ,  , хn – возможные значения дискретной величины;;
, хn – возможные значения дискретной величины;;
р1, р2,  , рn – соответствующие вероятности этих значений.
, рn – соответствующие вероятности этих значений.
Задание 2.
Найти дисперсию случайной величины Х – числа появлений события А в шести независимых испытаниях, если дано математическое ожидание М(х).
Указание: Написать биномиальный закон распределения вероятностей числа появлений события А в шести независимых испытаниях.
Биномиальное распределение вероятностей определяется формулой Бернулли:
Pn(k) = 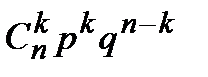
где n – число испытаний;
k – частота появления события А.
р – вероятность появления события А в испытаниях.
q – вероятность непоявления события А.
Аданне 3.
Дискретная случайная величина Х имеет три возможных значения х1, х2 , х3 , причем х1 < х2 < х3 . Вероятности того, что Х примет значение х1, и х2 соответственно равны р1 и р2.
Найти закон распределения величины Х, зная ее математическое ожидание М(х) и дисперсию D(х).
D(x) = 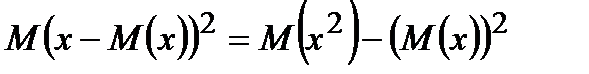
62
Вопросы:
1. Что такое математическое ожидание случайной величины?
2. Свойства математического ожидания.
3. Как рассчитать математическое ожидание дискретной случайной величины?
4. Что такое дисперсия дискретной случайной величины?
5. Свойства дисперсии.
6. Формулы расчета дисперсии.
7. Дисперсия числа появлений события в независимых испытаниях.
Вариант 1
1.
| X | 0,1 | 0,23 | 0,37 | 0,5 |
| P | 0,1 | 0,2 | 0,6 | 0,1 |
| Y | 3 | 8 | 12 | 24,30 |
| G | 0,15 | 0,25 | 0,2 | 0,4 |
2. M(x) = 4,2
3.
X1 = 5
P1 = 0,7
P2 = 0,2
M(x) = 5,4
D(x) = 0,44
Вариант 2
1.
| X | 12,100 | 13,20 | 14,30 | 15,40 | 16,50 |
| P | 0,1 | 0,13 | 0,22 | 0,17 | 0,38 |
| Y | 0,8 | 1,400 | 2,200 | ||
| G | 0,3 | 0,3 | 0,4 |
2.
M(x) = 2,4
3.
X1 = 1
P1 = 0,1
P2 = 0,7
M(x) = 2,1
D(x) = 0,29
63
Вариант 3
1.
| X | 3,2 | 5,6 | 6,7 | 7,3 | 8,8 |
| P | 0,28 | 0,01 | 0,32 | 0,27 | 0,12 |
| Y | 0,15 | 0,17 | 0,19 | ||
| G | 0,7 | 0,1 | 0,2 |
2. M(x) = 1,8
3.
X1 = 2
P1 = 0,2
P2 = 0,2
M(x) = 3,4
D(x) = 0,64
Вариант 4
1.
| X | 0,28 | 0,73 | 1,2 | 1,7 |
| P | 0,7 | 0,08 | 0,2 | 0,02 |
| Y | 2,35 | 10,8 | 15,11 | 16 |
| G | 0,1 | 0,13 | 0,44 | 0,33 |
2. M(x) = 1,2
3. X1 = 3
P1 = 0,5
P2 = 0,4
M(x) = 3,6
D(x) = 0,44
Вариант 5
1.
| X | 28,8 | 29,3 | 37,5 | 43,8 |
| P | 0,13 | 0,13 | 0,13 | 0,61 |
| Y | 0,2 | 0,81 | 0,905 | 1,03 |
| G | 0,5 | 0,2 | 0,1 | 0,2 |
2. M(x) = 3,6
3.
X1 = 4
P1 = 0,4
P2 = 0,4
M(x) = 4,8
D(x) = 0,56
64
Вариант 6
1.
| X | 18,1 | 20,1 | 25,1 | ||
| P | 0,4 | 0,3 | 0,3 | ||
| Y | 0,12 | 0,38 | 1,57 | 3,13 | 4,2 |
| G | 0,15 | 0,18 | 0,17 | 0,27 | 0,23 |
2. M(x) = 4,8
3. X1 = 5
P1 = 0,6
P2 = 0,1
M(x) = 5,7
D(x) = 0,81
Вариант 7
1.
| X | 0,3 | 0,8 | 1,2 | 1,3 | 3,7 |
| P | 0,1 | 0,3 | 0,1 | 0,15 | 0,35 |
| Y | 41,8 | 42,2 | 45,3 | ||
| G | 0,4 | 0,3 | 0,3 |
2.
M(x) = 1,2
3.
X1 = 2
P1 = 0,6
P2 = 0,1
M(x) = 2,7
D(x) = 0,81
Вариант 8
1.
| X | 0,3 | 0,81 | 1,2 | 1,8 |
| P | 0,3 | 0,5 | 0,1 | 0,1 |
| Y | 31,3 | 42,5 | 51,6 | 58,2 |
| G | 0,14 | 0,28 | 0,31 | 0,27 |
2. M(x) = 1,8
3. X1 = 3
P1 = 0,4
P2 = 0,3
M(x) = 3,9
D(x) = 0,69
65
Вариант 9
1.
| X | 0,2 | 0,32 | 0,88 | ||
| P | 0,2 | 0,2 | 0,6 | ||
| Y | 3,7 | 15,8 | 16,1 | 25,8 | 31,2 |
| G | 0,21 | 0,22 | 0,2 | 0,2 | 0,17 |
2.
M(x) = 2,4
3.
X1 = 1
P1 = 0,3
P2 = 0,2
M(x) = 2,2
D(x) = 0,76
Вариант 10
1.
| X | 20,2 | 30,8 | 41,3 | ||
| P | 0,3 | 0,45 | 0,25 | ||
| Y | 1,2 | 3,7 | 7,28 | 9,15 | 10 |
| G | 0,28 | 0,12 | 0,15 | 0,27 | 0,18 |
2.
M(x) = 3,6
3.
X1 = 4
P1 = 0,6
P2 = 0,1
M(x) = 4,7
D(x) = 0,81
66
Контрольная работа.
1 вариант.
1. В страховом обществе застрахованы 1000 автомобилистов. Вероятность аварии в течение года р=0,2. Найти вероятность того, что число аварий больше 195 и меньше 210.
2. В студии 3 телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера.
3. Случайная величина Х принимает возможные значения 1 и 3, образующие полную группу. М(Х)=2,3. Найти 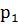 ;
; 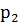 и дисперсию D(Х).
и дисперсию D(Х).
4. Событие А наступает с вероятностью р=0,3. Проведено 5 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 2 раза; б) не меньше двух и не больше четырёх раз.
2 вариант.
1. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.
2. На стоянке 5 машин. Найти вероятность того, что среди этих машин:
а) две легковые; б) Не меньше двух и не больше четырех легковых машин.
3. Вероятность того, что событие А появится хотя бы один раз при двух независимых испытаниях равна 0,75. Найти вероятность появления события в одном испытании.
4. Случайная величина Х принимает три возможных значения: 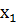 =1;
=1; 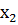 =2;
=2; 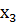 =3. Математическое ожидание этой величины равно 2,3; математическое ожидание её квадрата рано 5,9. Найти вероятность
=3. Математическое ожидание этой величины равно 2,3; математическое ожидание её квадрата рано 5,9. Найти вероятность 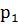 ;
; 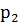 ;
; 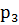
67
3 вариант.
1. Вероятность появления события в каждом из 300 независимых испытаний равна 0,8. Найти вероятность того, что событие появится не менее 245 раз.
2. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2-х деталей есть хотя бы одна стандартная.
3. Случайная величина Х принимает два возможных значения 1 и 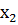 , образующих полную группу. Вероятности их 0,2 и
, образующих полную группу. Вероятности их 0,2 и 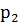 . Математическое ожидание М(Х) равно 3,4. Найти
. Математическое ожидание М(Х) равно 3,4. Найти 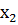 ;
; 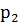 и дисперсию случайной величины.
и дисперсию случайной величины.
4. Событие А наступает с вероятностью р=0,4. Проведено 6 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 3 раза; б) не меньше трёх и не больше пяти раз.
4 вариант.
1. Монета брошена 200 раз. Найти вероятность того, что герб выпадет ровно 100 раз.
2. В коробке находится 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров.
Найти вероятность того, что среди них:
а) 3 белых шара;
б) меньше, чем 3 белых шара;
в) хотя бы 1 белый шар.
3. Случайная величина Х принимает два возможных значения 2 и 5,2, образующих полную группу. Известно математическое ожидание М(Х) равное 3,7. Найти вероятности 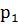 ;
; 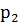 и дисперсию случайной величины.
и дисперсию случайной величины.
4. По каналу связи с одинаковыми вероятностями передаются 10 сигналов. Ввиду помех четыре из переданных сигналов при приеме искажаются. Найти вероятность того, что из двух наудачу взятых сигналов хотя бы один будет принят без искажений.
68
5 вариант.
1. Проведено 177 опытов. Вероятность появления положительного результата в каждом опыте равна р=0,9. Найти вероятность того, что не менее 150 и не более 160 опытов дадут положительный результат.
2. Событие А наступает с вероятностью р=0,35. Проведено 7 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 5 раз; б) не меньше трёх и не больше пяти раз.
3. Найти дисперсию случайной величины Х, заданной законом распределения:
| х | -5 | 2 | 3 | 4 |
| р | 0,4 | 0,3 | 0,1 | 0,2 |
4. Из 15 билетов выигрышными являются 4. Какова вероятность того, что среди двух билетов, взятых наудачу, есть хотя бы один выигрышный.
6 вариант.
1. Вероятность появления события в каждом из 100 независимых испытаний равна 0,8. Найти вероятность того, что событие появится не менее 75 раз.
2. Случайная величина Х принимает возможные значения: 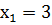 ;
; 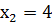 ;
; 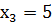 . Математическое ожидание этой величины равно 4,1; математическое ожидание её квадрата равно 17,7. Найти вероятности
. Математическое ожидание этой величины равно 4,1; математическое ожидание её квадрата равно 17,7. Найти вероятности 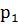 ;
; 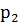 и
и 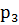 .
.
3. В группе спортсменов 6 человек. Вероятность присутствия среди них бегунов равна 0,25. Найти вероятность того, что среди этих спортсменов:
а) 3 бегуна; б) не меньше двух и не больше четырех бегунов.
4. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
69
7 вариант.
1. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
2. Событие А наступает с вероятностью 0,6. Проведено 4 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 3 раза; б) не меньше одного и не больше трёх раз.
3. Найти дисперсию случайной величины Х, заданной законом распределения:
| х | -2 | -1 | 1 | 2 |
| р | 0,5 | 0,4 | 0,3 | 0,2 |
4. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9364. Найти вероятность попадания в цель при одном выстреле.
8 вариант.
1. В страховом обществе застрахованы 1000 автомобилистов. Вероятность аварии в течение года р=0,3. Найти вероятность того, что число аварий больше 295 и меньше 310.
2. В студии 3 телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент равна 0,8. Найти вероятность того, что в данный момент включена хотя бы одна камера.
3. Случайная величина Х принимает возможные значения 1 и 5, образующие полную группу. М(Х)=4,3. Найти 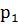 ;
; 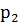 и дисперсию D(Х).
и дисперсию D(Х).
4. Событие А наступает с вероятностью р=0,4. Проведено 5 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно 3 раза; б) не меньше трех и не больше четырёх раз.
70
9 вариант.
1. Вероятность рождения девочки равна 0,49. Найти вероятность того, что среди 100 новорожденных окажется 50 девочек.
2. На стоянке 4 машины. Найти вероятность того, что среди этих машин:
а) две легковые; б) не меньше двух и не больше трех легковых машин.
3. Вероятность того, что событие А появится хотя бы один раз при трех независимых испытаниях равна 0,936. Найти вероятность появления события в каждом из испытаний при условии, что она постоянна.
4. Случайная величина Х принимает три возможных значения: 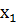 =1;
=1; 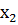 =2;
=2; 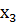 =3. Математическое ожидание этой величины равно 1,9; математическое ожидание её квадрата рано 4,3. Найти вероятность
=3. Математическое ожидание этой величины равно 1,9; математическое ожидание её квадрата рано 4,3. Найти вероятность 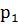 ;
; 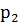 ;
; 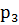
10 вариант.
1. Вероятность появления события в каждом из 200 независимых испытаний равна 0,8. Найти вероятность того, что событие появится не менее 155 раз.
2. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2-х деталей есть хотя бы одна стандартная.
3. Случайная величина Х принимает два возможных значения 1 и 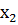 , образующих полную группу. Вероятности их 0,2 и
, образующих полную группу. Вероятности их 0,2 и 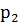 . Математическое ожидание М(Х) равно 1,4. Найти
. Математическое ожидание М(Х) равно 1,4. Найти 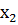 ;
; 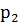 и дисперсию случайной величины.
и дисперсию случайной величины.
4. Событие А наступает с вероятностью р=0,3. Проведено 5 независимых испытаний. Найти вероятность того, что событие наступит:
а) ровно четыре раза; б) не меньше двух и не больше четырёх раз.
71
Практическая работа № 3.
Задание 1.
Составить вариационный ряд по данным протокола наблюдений.
Вычислить относительные частоты. Результаты занести в таблицу:
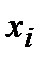
| 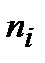
| 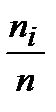
| |
где n – объём выборки;
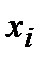 – значения элементов выборки;
– значения элементов выборки;
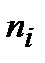 – частота повторения i-го значения;
– частота повторения i-го значения;
Wi = 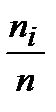 – относительная частота.
– относительная частота.
Задание 2.
Построить графики вариационного ряда: (полигон частот и гистограмму относительных частот).
Задание 3.
Составить эмпирическую функцию распределения
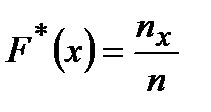
где n – объём выборки;
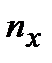 – число вариант, меньших х.
– число вариант, меньших х.
Задание 4.
Построить график эмпирической функции распределения.
Вопросы:
1. Что такое генеральная и выборочная совокупности?
2. Как составить вариационный ряд?
3. Чему равен объём выборки?
4. Что такое относительная частота?
5. Статистическое распределение выборки.
6. Графики вариационного ряда.
7. Эмпирическая функция распределения и её свойства.
72
Вариант 1
| 4 | 6 | 0 | 2 | 1 | 3 | 3 | 1 | 2 | 5 | 3 | 1 2 | 2 | 4 | 4 | 4 | 3 | 2 | 5 |
| 2 | 5 | 1 | 2 | 3 | 0 | 3 | 0 | 5 | 1 | 2 | 1 3 | 0 | 4 | 0 | 2 | 2 | 1 | 0 |
| 5 | 1 | 4 | 2 | 4 | 2 | 1 | 3 | 1 | 0 | 6 | 1 2 | 1 | 4 | 2 | 2 | 0 | 2 | 4 |
2212 2
n = 65
начало первого интервала: 0 длина интервала: 1
Вариант 2
| 0 0 | 0 | 1 | 0 | 0 | 1 | 3 | 1 | 1 | 1 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 0 | 1 |
| 1 1 | 1 | 3 | 2 | 0 | 0 | 1 | 4 | 1 | 0 | 0 | 0 | 2 | 0 | 1 | 2 | 1 | 2 | 0 |
| 1 2 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 2 | 0 | 1 | 0 | 0 | 0 | 2 |
| 1 2 | 0 | 1 | 1 | 1 | 2 | 0 | 0 | 2 | 1 | 1 | 2 | 2 | 0 | 0 | 0 | 2 | 0 | 0 |
010 0
n = 84
начало первого интервала: 0 длина интервала: 1
Вариант 3
| 4 | 1 | 9 | 6 | 11 | 11 | 6 | 5 | 10 | 4 | 10 | 10 | 12 | 10 | 9 |
| 6 | 6 | 8 | 4 | 10 | 2 | 5 | 6 | 8 | 6 | 7 | 2 | 2 | 6 | 12 |
| 2 | 8 | 8 | 11 | 9 | 6 | 7 | 4 | 5 | 9 | 7 | 9 | 5 | 9 | 10 |
| 5 | 8 | 6 | 10 | 8 | 8 | 6 | 9 | 10 | 8 | 6 | 1 | 3 | 10 | 4 |
| 8 | 6 | 10 | 9 | 10 | 3 | 6 | 11 |
n = 68
начало первого интервала: 1 длина интервала: 1
Вариант 4
| 2 | 0 | 2 | 6 | 2 | 3 | 5 | 3 8 | 3 | 6 | 4 | 5 | 2 | 6 | 6 | 5 | 5 | 8 | 8 |
| 3 | 5 | 3 | 2 | 4 | 5 | 2 | 1 6 | 9 | 7 | 6 | 7 | 4 | 5 | 6 | 5 | 6 | 8 | 3 |
| 6 | 5 | 5 | 1 | 7 | 6 | 4 | 1 5 | 6 | 4 | 7 | 2 | 8 | 8 | 2 | 8 | 2 | 1 | 6 |
n = 60
начало первого интервала: 0 длина интервала: 1
Вариант 5
| 2 | 0 0 | 3 | 1 | 2 2 | 2 | 3 | 4 | 1 | 2 | 3 | 3 | 2 | 1 1 | 3 3 | 0 |
| 4 | 1 3 | 3 | 0 | 1 0 | 0 | 1 | 2 | 1 | 1 | 3 | 2 | 3 | 0 1 | 0 4 | 2 |
| 3 | 1 2 | 1 | 1 | 1 1 | 2 | 1 | 2 | 5 | 2 | 1 | 3 | 2 | 3 1 | 1 1 | 1 |
| 2 | 1 1 | 1 | 3 | 1 3 | 1 | 2 | 1 | 2 | 1 | 1 | 0 | 0 | 3 3 | 1 2 | 3 |
n = 80
начало первого интервала: 0 длина интервала: I
73
Вариант 6
7 1 1 555594 5385383
11 3 9683362744357
4 6529586 11774497
431664545578684 1
0 277596112779268
n = 80
начало первого интервала: 0 длина интервала: 1
Вариант 7
| 1 | 0 | 1 | 3 | 1 | 1 | 4 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 2 | 1 | 0 1 |
| 1 | 0 | 1 | 0 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | 1 | 2 | 1 | 1 | 1 | 2 | 3 | 0 1 |
| 0 | 2 | 2 | 0 | 2 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 1 | 2 | 0 1 |
| 2 | 1 | 1 | 0 | 1 | 2 | 0 | 2 | 2 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 3 | 1 | 2 2 |
| 2 | 0 | 2 | 0 | 2 | 1 | 0 | 3 | 1 | 1 | 3 |
n = 91
начало первого интервала:0 длина интервала: 1
Вариант 8
| 1 | 4 | 3 | 3 | 1 | 0 | 4 | 0 | 4 | 3 | 2 | 0 | 2 | 2 | 3 | 3 | 1 0 | 3 | 3 |
| 3 | 2 | 3 | 1 | 3 | 2 | 5 | 6 | 3 | 2 | 5 | 2 | 3 | 4 | 2 | 3 | 2 2 | 6 | 2 |
| 0 | 1 | 2 | 3 | 6 | 2 | 1 | 4 | 3 | 3 | 1 | 5 | 4 | 3 | 2 | 1 | 1 1 | 6 | 1 |
| 2 | 0 | 2 | 2 | 2 | 3 | |||||||||||||
n = 66
начало первого интервала:0 длина интервала: 1
74
Вариант 9
| 4 | 5 | 3 | 4 | 5 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 3 | 1 | 4 | 1 | 4 | 5 | 5 | 1 |
| 2 | 5 | 5 | 5 | 3 | 4 | 3 | 5 | 5 | 4 | 0 | 2 | 6 | 7 | 1 | 3 | 2 | 2 | 4 | 2 |
| 3 | 3 | 6 | 0 | 6 | 2 | 4 | 1 | 6 | 1 | 5 | 4 | 4 | 4 | 5 | 2 | 4 | 5 | 3 | 5 |
| 5 | 6 | 2 | 2 | 3 | 2 | 2 | 5 | 2 | 5 | 5 | 0 | 7 | 1 | 0 | 0 | 0 | 5 | 5 | 2 |
7 6 3 5 3
n = 85
начало первого интервала:0 длина интервала: 1
Вариант 10
| 7 | 8 | 4 | 0 | 4 | 6 | 5 | 4 | 3 | 2 | 4 | 8 | 6 | 2 | 2 |
| 5 | 3 | 6 | 6 | 5 | 5 | 3 | 5 | 6 | 7 | 8 | 9 | 5 | 2 | 5 |
| 4 | 5 | 6 | 6 | 3 | 6 | 5 | 4 | 5 | 10 | 3 | 7 | 5 | 3 | |
| 3 | 3 | 7 | 5 | 3 | 4 | 9 | 2 | 1 | 4 | 4 | 4 | 2 | 4 | 3 |
| 4 | 4 | 5 | 5 | 3 | 7 | 5 | 3 | 2 | 6 | 2 | 4 | 4 | 4 | 0 |
| 6 | 1 | 1 | 4 | 4 | 5 | 4 | 8 | 3 | 5 | 5 | 4 | 1 | 9 |
n=89
начало первого интервала: 0 длина интервала: 1
75
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы.
Основные источники:
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Юрайт, 2016.
2. Ш.А. Алимов и др. Алгебра и начала математического анализа 10-11 класс. – М.: Просвещение, 2016.
Дополнительные источники:
1. Колде Я.К. Практикум по теории вероятностей и математической статистике. – М.: Высшая школа, 1991.
2. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. – М.: Академия, 2003.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Юрайт, 2016.
4. Интернет-ресурсы:
mathprofi.ru
www.matburo.ru
www.lektorium.tv
Желаем успехов!
76
по предмету «Теория вероятностей и математическая статистика».
09.02.03. «Программирование в компьютерных системах»
Для студентов заочного отделения.
Санкт-Петербург
2018 год
| РАССМОТРЕНЫ: предметной (цикловой) комиссией математики и физики Протокол № ____ от «______» ____________2018 г. Председатель ПЦК Е.В. Кудрявцева ___________________________ подпись | УТВЕРЖДАЮ: Зам. Директора по УМР ____________Е.Г. Конакина «___»______________2018 г. |
| Рекомендованы Методическим советом УПК СПбПУ Протокол №___ от «___» __________2018 г. Старший методист О.М. Симонова ___________________ подпись |
Зам. директора по УМР
Е.Г. Конакина ___________________
подпись
Методические рекомендации по выполнению практических работ и контрольной работы разработаны на основе Федеральных государственных образовательных стандартов (далее – ФГОС) по специальности среднего профессионального образования (далее - СПО) 09.02.03 «Программирование в компьютерных системах» и учебных планов Университетского политехнического колледжа федерального государственного автономного образовательного учреждения высшего образования «Санкт-Петербургский политехнический университет Петра Великого».
Разработчик: Ю. А. Муравьёва, преподаватель УПК СПбПУ
Пояснительная записка.
Методические указания к выполнению внеаудиторной самостоятельной работы студентов по дисциплине «Теория вероятностей и математическая статистика» предназначены для студентов заочного отделения 2-го курса по специальности 09.02.03. «Программирование в компьютерных системах».
Цель методических указаний: оказание помощи студентам в выполнении практических работ и контрольной работы по дисциплине «Теория вероятностей и математическая статистика».
В результате изучения дисциплины студент
Должен знать:
- основы теории вероятностей;
- основы математической статистики.
Должен уметь:
- вычислять вероятность событий с использованием элементов комбинаторики;
- использовать методы математической статистики.
В результате освоения учебной дисциплины у обучающегося формируются общие и профессиональные компетенции:
- ОК 1 – Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
- ОК 2 – Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
- ОК 3 – Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
- ОК 4 – Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
- ОК 5 – Использовать информационно-коммуникационные технологии в профессиональной деятельности.
- ОК 6 – Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
3
- ОК 7 – Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
3
- ОК 8 – Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
- ОК 9 – Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
- ПК 1.1 – Выполнять разработку спецификаций отдельных компонент.
- ПК 1.2 – Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля.
- ПК 2.4 – Реализовывать методы и технологии защиты информации в базах данных.
- ПК 3.4 – Осуществлять разработку тестовых наборов и тестовых сценариев.
Знания по дисциплине приобретаются студентами в процессе проведения занятий и в процессе самоподготовки.
Умения формируются при решении практических работ.
В данном пособии даны рекомендации по оформлению практических работ и контрольной работы, литература для самостоятельного изучения студентами, вопросы для самопроверки, образцы решения задач стандартного вида.
При выполнении практических работ и контрольной работы студент должен руководствоваться следующими указаниями:
1. Контрольная работа и практические работы выполняются в отдельной тетради в клетку, на титульном листе которой должны быть ясно написаны фамилия студента, его инициалы, курс, специальность, e-mail, сотовый телефон, домашний адрес.
2. Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать ее условие.
3. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
4
4. Контрольная работа и практические работы выполняются самостоятельно.
5. В случае незачета по контрольной работе или по практическим работам студент обязан в кратчайший срок исправить все отмеченные ошибки и предоставить работы на повторную проверку.
6. Студент выполняет тот вариант, который совпадает с его номером в журнале. Варианты практических работ и контрольной работы представлены в приложении.
Перед выполнением практических работ и контрольной работы студент должен изучить соответствующие разделы курса “Теория вероятностей и математическая статистика”, используя учебные издания, Интернет-ресурсы, дополнительную литературу и составить конспект. Выполнить практические задания, ответить на вопросы.
Список рекомендуемой литературы приведен в методических указаниях. Студент может использовать также учебники и учебные пособия, не включенные в данный список, если эти пособия содержат соответствующие разделы учебного курса.
Однако, в случае возникновения затруднений при самостоятельном изучении материала, студент может обратиться к преподавателю теории вероятностей и математической статистики для получения устной консультации.
Конспект – это краткое изложение или краткая запись содержания.
Требования к конспекту: системность, логичность изложения, краткость, убедительность и доказательность.
Этапы конспектирования:
1. Прочитайте текст, отметьте в нем непонятные места, новые термины, перечислите основные мысли текста, составьте план.
2. Выясните значение новых непонятных терминов и символов.
3. Вторичное чтение сочетайте с записями основных мыслей. Запись ведите своими словами, не переписывайте текст дословно.
Правила записи текста:
1. Запись должна быть компактной.
5
2. В тексте необходимо применять выделения и разграничения: подчеркивание (для выделения заголовка и подзаголовка, выводов, отделения одной темы от другой, одного вопроса от другого); красную строку для обозначения абзацев и пунктов плана; нумерацию абзацев; выделение с помощью рамки определений, правил, законов, формул и так далее.
3. При записи допускается пользоваться сокращениями.
4. Сформулируйте и запишите вывод.
Цель написания практических работ и контрольной (домашней) работы - оценить освоенные умения и усвоенные знания.
Порядок выполнения самостоятельной работы:
Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надёжности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках.
Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приёмочном контроле качества продукции и для многих других целей.
Дата: 2018-11-18, просмотров: 712.