Положим, что на вход четырехполюсника, имеющего переходную функцию h ( t ), воздействует синусоидальное напряжение единичной амплитуды u ( t ) = I sin ωt = Im ejωt. Тогда, используя формулу интеграла Дюамеля, определим: напряжение на выходе четырехполюсника:
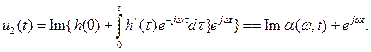 (a)
(a)
Здесь:
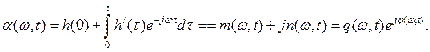 (б)
(б)
где a (ω t ) - огибающая выходного напряжения при воздействии синусоидального u 1 ( t ). Воздействуем на вход четырехполюсника амплитудно-модулированным синусоидальным напряжением
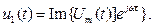 и определим:
и определим:
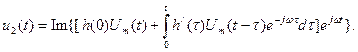
Учтем, что:……… 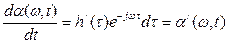 и
и 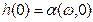 . Тогда:
. Тогда:
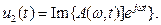 (в)
(в)
где: 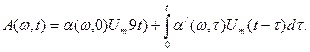 (в)
(в)
A (ω t ) - огибающая выходного напряжения. Формулу (г) называют интегралом мюамеля для огибающей, она позволяет, не вдаваясь в мелкие детали, выявить макроструктуру переходного процесса.
Вопросы для самопроверки
1. Дайте определение переходному процессу.
2. Что понимают под принужденными и свободными токами и напряжениями?
3. Сформулируйте законы (правила) коммутации.
4. Дайте определение зависимым и независимым начальным условиям.
5. Какие вы знаете способы составления характеристического уравнения.
6. Объясните, почему при составлении характеристического уравнения путем приравнивания нулю входного сопротивления Z ( p )= N ( p )/ M ( p ) в общем случае нельзя сокращать числитель и знаменатель дроби на общий множитель.
7. Чем определяется число корней характеристического уравнения?
8. Изложите сущность классического метода расчета и принцип составления уравнений для определения постоянных интегрирования.
9. Переходный процесс в некоторой цепи сопровождается биениями. О чем это может свидетельствовать?
10. Дайте обоснование обобщенным законам коммутации.
11. Запишите известные вам соотношения между f ( t ) и F ( p ), а также теоремы операторного метода и предельные соотношения.
12. Почему р называют комплексной частотой?
13. Охарактеризуйте этапы расчета операторным методом.
14. В чем особенности расчета переходных процессов операторным методом при синусоидальном источнике и ненулевых начальных условиях?
15. Охарактеризуйте свойства единичной функции 1(/) и свойства дельта-функции δ( t ).
16. Определите переходную и импульсную переходную проводимости (сопротивления) и функции. Укажите, с какой целью они используются.
17. Охарактеризуйте идею расчета с помощью интеграла Дюамеля.
18. Прокомментируйте известные вам формы записи интеграла Дюамеля.
19. Какими способами можно определить отзвук системы, когда на нее воздействует импульс напряжения или тока?
20. Поясните принцип работы интегрирующих и дифференцирующих цепей. Запишите условия, при которых эти цепи выполняют свои функции.
21. Чем следует руководствоваться при формировании дополняющих двухполюсников?
22. Поясните идею расчета переходных процессов с помощью обобщенных функций.
23. Перечислите основные этапы расчета методом переменных состояния.
24. Как составляют уравнения переменных состояния путем сведения послекоммутационной схемы к чисто резистивной?
25. Охарактеризуйте сильные и относительно слабые стороны известных вам методов расчета переходных процессов.
26. Что понимают под системными функциями? Какие виды чувствительности системных функций вы знаете?
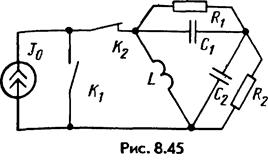
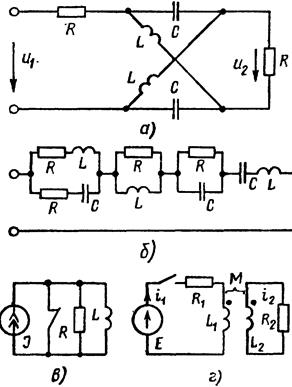
Рисунок 8.46
27. В схеме рисунок 8.45 с источником тока I 0 в момент t = 0 одновременно размыкается ключ K 2 и замыкается K 1. Показать, что заряды, протекшие через сопротивление R 1 и R 2 за время от 0 до ∞, не зависят от емкостей С1 и С2. Определить величины этих зарядов. (Ответ: 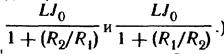
J29. Покажите, что в симметричной мостовой схеме (рис. 8.46, а), в которой выполняется условие L/C = R 2 , переходная
I -7'
функция h ( t ) = — — + е .
30. В схеме рис. 8.46, 6 R = L = С = 1. Покажите, что
входная переходная проводимость равна te ~ *.
31. Покажите, что энергия, запасаемая в L схемы рис. 8.46, в (начальные условия нулевые), равны тепловым потерям в R .
32. Первичная обмотка трансформатора рис. 8.46, г при нулевых начальных условиях подключается к источнику постоянной ЭДС Е, Rx = /?2 = R; Lx = L2 = М.
Определите ij(0_|_), i2(0_j_). [Ответ i,(0+) = —i2(0+) = E /(2 R ).]
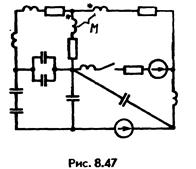
33. Определите степень характеристического уравнения для схемы рис. 8.47.(Огвет — пятая.)
34. Как определить К(р) через h ( t ) и через h (f)?
35. По h ( t) = 4(1 + 2е
ника определите его /((/со). (Ответ: )
36. По К(/со) = „
3 R + /coL _ RC ^ L + /coL
некоторого четырехполюсника определите его h ( t) при R — 0,2 Ом, С = 5 Ф, L = 1 ^Н- (Ответ: h ( t )= 1,62е—°’724* — 0,62е~ 0,276#.)
37. На вход четырехполюсника с
( d /d\"i / d /DT-)
38. В схеме рис. 8.4, в при размыкании ключа происходит переходный процесс. Определить законы изменения во времени напряжений исх и ыс2 на конденсаторах. Задано/(f) = lsin(cof + 90°) A, R = 1/соС = 1 Ом; со = 100 рад/с.
0,253 — 0,15е
(/<■>) = ГТ1Г воздействует единичный импульс напряжения в виде 6-функции 1 -f- /2ш
Определите напряжение на выходе четырехполюсника после окончания действия
импульса. (Ответ: 0,25е 0,5/.)38.
Решите задачи 11.4; 11.12; 11.15; 11.26; 11.29; 11.32; 11.38; 11.40; 11.47; 11.50; 11.55; 11.57.
ПРИЛОЖЕНИЕ 1
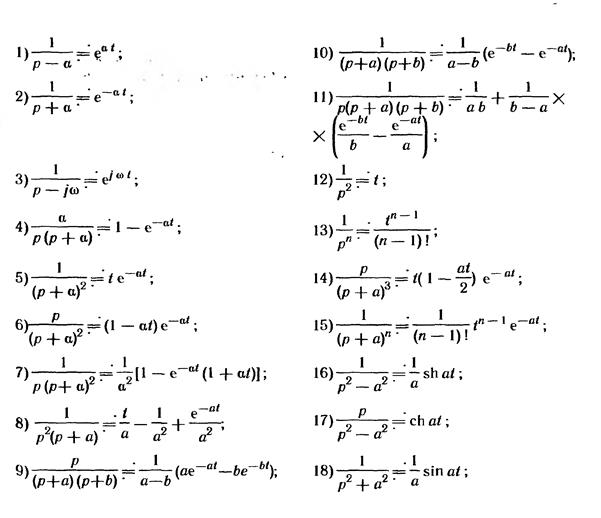

ЗАДАНИЯ
Пример 80.
В схеме рис. 8.17 до замыкания ключа был установившийся режим: R \ ~ R \' = /?з = 50 Ом; С = 100 мкФ; Е — 150 В. Требуется найти: 1) полные, принужденные и свободные составляющие токов i \, *2, /3 и ис при t = 0+, а также
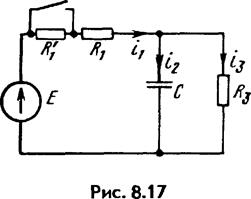
Рисунок -
начальное значение производной от свободного напряжения на конденсаторе; 2)токи t'l, *2, ("з и напряжение ис в функции времени.
Решение первой части задачи. До коммутации «2(0_) = О и ij(0_) = i'3(0_J = E /{ RX + + R 3) — 150/150 = I A.
Напряжение на конденсаторе равно напряжению на резисторе R ^- ис(0_) = 13(0_)/?3 = 1 • 50 = 50 В.
Найдем принужденные значения токов и напряжений после коммутации:
<1„р = 'з,ф = E /( R, + R 3 ) = 150/100 = 1,5 А; мСпр(°+) = W°+>*3 = 1,5 ■ 50 = 75 В.
По второму закону Кирхгофа составим уравнение для контура, образованного первой и второй ветвями при t — 0_|_:
*1(0+)Я| + М°+) = но М°+)= М0-)-
Поэтому
Е — ыс(0_) 150-50
«0+) = —
Из уравнения wc(0+) = *3(0+)/?3 получим
Ф+) = «с(®+)/ Я3 = 1 А.
По первому закону Кирхгофа ^(О^) = + *з(®+)‘ Следовательно,
*2(0+) = 4(0+) - ‘з(°+) = 2 - 1 = 1 А.
Свободные составляющие тока и напряжения при t = 0_|_ определим как разности между полными и принужденными величинами:
“с 0,(0+) = М°+) - “с „Р<°+) = 50 — 75 = — 25 В; i,c„(0+) = '[(О-)-) (1 ,ф(0+) = 2 1,5 = 0,5 А;
HbJf >+) = %№+) - W°+> = 1 - 0 = 1 А; ■'зс»(0+) = Ф+) ~ <злР(0+) = 1 - 1,5 = - 0,5 А.
Так как свободный ток через конденсатор
йис св
*св = С то 6и с = l JC -
В рассматриваемом примере
(<Чсв/<»), = о+ = 'W°+)/C = '/(100.КГ6) = Ю4 В/с.
Решение второй части задачи. Характеристическое уравнение для послекоммутационной схемы pR ^ R ^ C -f- /?, -f- R 3 = 0 имеет один корень
I
' —ад^=-400с
Каждый ток равен сумме принужденной и свободной составляющей Aept, гдеЛ равно значению свободной Составляющей при t — 0_|_ (рис. 8.18):
j, = 1,5 + 0,5е~ 400' A; i 2 = е~ 400< А;
/3 =1,5 — 0,5е“ ти А; ис = 75 - 25е~ 4001 В.
Пример 81.
В схеме рис. 8.19 до замыкания ключа был установившийся режим-
Пример 88. В схеме рис. 8.29 при нулевых начальных условиях замыкают ключ, доставить операторные изображения юков п и /з, пользуясь методом контчрных токов.
Пример 94. Определить юк «'1(0 в схеме рис. 8.17 с помощью формулы разложения и сравнить с результатом решения классическим методом (см. пример 80), если Е = 150 В; R = ЯГ = /?3 = 50 Ом; С = 100 мкФ; ые(0) = 50 В.
Решение. Составим послеком мутационную операторную схему (рис. 8.32), имея в виду, что начальные условия ненулевые. Внутренняя ЭДС «с(0)/р позволяет учесть, что до коммутации конденсатор был заряжен до напряжения ис(0) током ф rum ом у она направлена встречно току /2 (р). Узел 0 схемы заземлим. Потенциал узда / обозначим yi ( p ) и определим ei о по методу узловых потенциалов: о
Мнимую, а недействительную часть из формулы разложения берут потому, чТ° заданная ЭДС £msin(t»< -f- ^) есть мнимая часть комплекса
Пример 101. Найти ii = f ( t ) и ич = f ( t ) при замыкании ключа из схеме рис. 8.37, а.
Напряжение источника ЭДС u ( t ) = 100 (1 — е~а<)В; а = 0,25 с~*; R = 0,5 Ом; Li — = 1 Гн; М = 0,5 Гн.
Решение. Переходная проводимость цепи, состоящей из последовательно
включенных R и L , g ( t ) — — (1 — e ~ bt ), где
R
ь - Я/L,; at ~ 1) = ^l1 - е-‘«-х>].
Первое слагаемое в формуле (8.63) выпадает, так как и (0) = 0. При этом и' (/) = ^7 I00 (1 — e ~ Gt ) = Ю0ае~а<; и' (т) = 100а е-ат;
Пример 107. Путем использования обобщенных функций решить задачу примера 86(см. рис. 8.24).
Решение. В уравнении для послеком мутационной схемы
rfr d"C1 Л Г dUC 2 l Г
At +С2-1Г]+"С1 = £
подставим
u ci = «С1-(0Н- 0 + «ci+(0H0; «сг = «С2-(0Н— 0 + «С2+(*)Ц0;
Дата: 2018-11-18, просмотров: 919.