Дельта-функцией δ( t ) или единичным импульсом (рисунок 13, а) называют прямоугольный импульс амплитудой 1/Δτ и длительностью Δτ при Δτ → 0. Единичным называют потому, что площадь его равна единице: - 1/ Δτ Δτ = 1. Размерность δ( t ) - с^-1.

Единичной функцией 1(0 (рисунок 13, б) называют функцию, равную единице при t > 0 и равную нулю при t < 0. Единичная функция 1(- t )(рисунок 13, в) равна нулю при t > 0 и единице при t < 0 . Функции 1 ( t ) и 1(-t ) имеют нулевую размерность. Свойства δ( t ):

1. из определения δ( t ) следует, что:

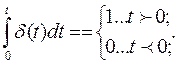
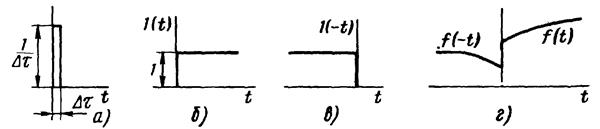
Рисунок 13

2. производная функции 1( t ) равна δ - функции:

dl ( t ) / d t = δ (0);

3. δ -функция обладает фильтрующим действием:

f(t) δ (t – t₁) = f(t₁) δ (t – t₁),

4.изображение по Лапласу δ -функции равно 1:

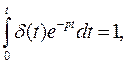 а

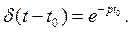
на основании теоремы смещения.

Единичные функции 1(t) и 1(-t) также обладают фильтрующим действием. Умножение произвольной функции f ( t ) на 1( t ) обращает произведение f ( t ) на 1( t ) в нуль при t < 0. Аналогично,

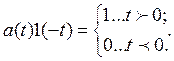
Импульсное (игольчатое) напряжение или ток в виде δ-функции единичной площади записывают так: δ ( t )- 1. Здесь единица имеет размерность В с или А с соответственно.

В соответствии с рисунком 13, а импульсное напряжение единичной площади, равное δ(t)-1 В с, можно представить как сумму двух прямоугольных импульсов: импульса напряжения 1/Δτ, вступающего в действие при t = 0, и импульса - (1/Δτ), вступающего в действие при t = Δτ.

При t ˃ Δτ и нулевых начальных условиях ток на входе цепи при -воздействии на нее напряжения в виде δ -функции:

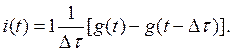
Разложив g ( t - Δτ) в ряд Тейлора по степеням Δτ и учитывая малость Δτ, получим:

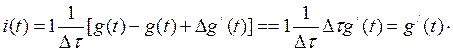
где 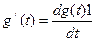 - импульсная переходная проводимость. Для моментов времени t > Δτ она численно равна току в цепи при воздействии на цепь напряжения в виде δ -функции.

Аналогично, 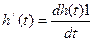 - импульсная переходная функция.

Для t > Δτ → 0 она численно равна напряжению на выходе четырехполюсника при воздействии на его вход импульса напряжения δ(t) 1 В с. В интервале времени от 0_ до 0₊ (во время действия импульса):

u ₂ ( t ) = h '( t)•l+ h(0₊) δ(t) = h ^δ(t ).

Наряду с понятиями ’’переходная проводимость” g ( t ) и ’’импульсная переходная проводимость” g '( t ) применяют дуальные понятия: переходное сопротивление r ( t ) и импульсное переходное сопротивление r '( t ). Переходное сопротивление r_ab ( t ) численно равно напряжению на входе цепи u_ab ( t ) при воздействии на ее вход единичного тока:

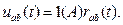
Импульсное переходное сопротивление r ' _ab ( t ) численно равно напряжению на входе цепи u_ab ( t ) после того как на ее вход воздей­ствовал импульс тока в виде δ-функции единичной площади:

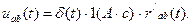
Величины r ( t ) и r '( t ) могут быть входными и взаимными, однако g ( t ) nR ( t ) не являются взаимно обратными величинами; g ( t ) определяется при питании схемы от источника ЭДС, a R ( t ) - при питании схемы от источника тока.

Подчеркнем, что в литературе по переходным процессам в зависимости от рассматриваемого вопроса под одним и тем же названием - импульсная переходная функция - понимают либо функ­цию h '( t), либо h ( t ). Между этими функциями имеется зависимость

h ^δ ( t ) = h (0₊) δ ( t )+ h ^/ ( t );

h '( t ) характеризует реакцию четырехполюсника (его выходное напряжение) после окончания воздействия на его вход единичным импульсом напряжения 1 - δ( t ) В с, a h ^δ t ) - напряжение на выходе четырехполюсника и во время действия импульса и после окончания.

Аналогичные соотношения существуют между двумя импульс­ными переходными проводимостями:

g^δ ( t ) = g (0₊) δ ( t )+ g ^/ ( t );

и между двумя импульсными переходными сопротивлениями:

R ^δ ( t ) = R (0₊) δ ( t )+ R ^/ ( t );

при воздействии на вход схемы единичным импульсом тока. С по­мощью h \ t ) интеграл Дюамеля запишется так:

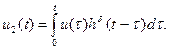
Здесь:

h^δ ( t - τ) == h ( 0) δ( t ) + h ' ( t - τ).

Формулу интеграла Дюамеля в математических работах называют формулой свертки двух функций в данном случае функций u ( t ) и h^δ ( t ).

7.38. Определение h ( t ) и h \ t ) через К(р).

Как упоминалось, при воздействии на вход четырехполюсника единичного напряжения u ₁ ( t )=1( t ) напряжение на выходе его u ₂ ( t )= h ( t ). Если это положение записать относительно изображений, учитывая, что 1( t )==1/p - и обозначив изображение h ( t ) через Н(р) то H (р)=К(р)/р.

Отсюда:

К(р) == рН(р).                              (7.47)

Определим теперь h ( t ) через К(р). Поскольку h ( t ) = = Н(р), а Н(р) определено предыдущей строкой, то:

h ( t ) == K ( p )/ p.                                    (7.48)

При воздействии на вход четырехполюсника единичным импульсом напряжения u ₁ ( t ) = 1 δ ( t ) == 1 = и₁(р), напряжение на выходе его:

u ₂ ( t ) = h^δ ( t ) == U ₁(р)К(р) = 1•К(р),

таким образом

h^δ ( t ) == K ( p ) .                           (7.49)