При подключении линейной электрической цепи с нулевыми начальными условиями к источнику постоянного напряжения U между какими-то двумя точками а и в схемы возникает напряжение u_ab(t), являющееся функцией времени и пропорциональное воздействующему напряжению U :

и_ав ( t) = Uh ( t) .                             (7.45а)

где h ( t ) - переходная функция. Это безразмерная величина, чис­ленно равная напряжению между точками а и в схемы, если на ее вход подать постоянное напряжение в 1 В; h ( t ), так же как и g ( t ), можно определить расчетным либо опытным путем.

Интеграл Дюамеля.

Познакомимся с третьим методом расчета переходных процессов в линейных электрических цепях - расчетом с помощью интеграла Дюамеля.

При использовании интеграла Дюамеля переменную, по кото­рой производится интегрирование, обозначим т, а под t по-прежнему будем понимать тот момент времени, в который требуется найти ток в цепи. Пусть к цепи с нулевыми начальными условиями в момент времени t = 0 подключается напряжение u (τ)(рисунок 8).

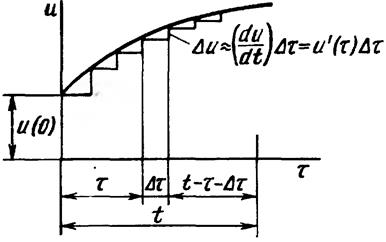
Рисунок 8

Для того чтобы найти ток в цепи в момент времени t , заменим плавную кривую ступенчатой и просуммируем токи от начального напряжения и(0) и от всех ступенек напряжения, вступающих в действие с запозданием во времени.

Напряжение и(0) в момент времени t вызовет в цепи ток

и(0)g( t ) где g (t) - переходная проводимость. В момент времени

τ + Δτ (рисунок 8) возникает скачок напряжения:

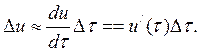
Для того чтобы найти составляющую тока в момент времени t , вызываемую этим скачком напряжения Aw, необходимо и'(τ) Δτ ум­ножить на значение переходной проводимости с учетом времени действия скачка до момента времени t . Из рисунка 8. видно, что это время равно t - τ - Δτ. Следовательно, приращение тока от этого скачка составляет и'( τ)g ( t - τ - Δτ) Δτ.

Полный момент времени t получим, если просуммируем все частичные токи от отдельных скачков и прибавим их к току

u (0) g ( t ):

i ( t ) =и(0 ) g ( t) + Σu /( τ ) g ( t - τ - Δτ ) Δτ.

Число членов суммы равно числу ступенек напряжения. Оче­видно, что ступенчатая кривая тем лучше заменяет плавную кри- вую, чем больше число ступенек. С этой целью заменим конечный интервал времени Δτ на бесконечно малый dτ и перейдем от суммы к интегралу:

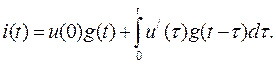                      (7.46)

Формулу (7.46) называют интегралом Дюамеля.

С помощью интеграла Дюамеля можно найти не только ток, но и любую другую физическую величину, например напряжение. В этом случае в формуле вместо переходной проводимости g(t ) будет входить переходная функция h(t), если на входе цепи действует источник ЭДС (напряжения), и переходное сопротивление R(t ) если на входе цепи действует источник тока.