На рисунке 7.3 изображена часть сложной разветвленной электрической цепи. Между узлами аи b этой цепи включена ветвь, содержащая R , L , C и источник ЭДС e ( t ). Ток по ветви обозначим через i .

Замыкание ключа К в схеме приводит к переходному процессу. До коммутации ток i = i (0_) и напряжение на конденсаторе и_с = = u _с (0_). Выразим потенциал точки а через потенциал точки b для послекоммутационного режима:

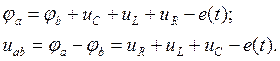
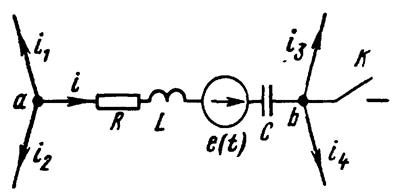
Рисунок 7.3

Вместо u _L запишем 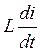 - вместо u_c соответственно  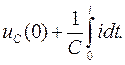 Тогда:

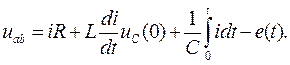                  (7.23)

 К уравнению (7.23) применим преобразование Лапласа. Преоб­разование Лапласа является линейным, поэтому изображение суммы равно сумме изображений.

Каждое слагаемое уравнения (7.23) заменим операторным изо­бражением: вместо iR запишем R I ( p )\ вместо u_ah - U_ah (р):

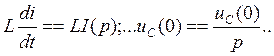
В результате найдем:

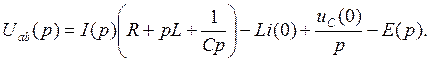(7.24)

Смысл проведенного преобразования состоит в том, что вместо дифференциального уравнения (7.23) получили алгебраическое уравнение (7.24), связывающее изображение тока 1(р) с изображе­нием ЭДС Е(р) и изображением напряжения U_ab ( p ). Из уравнения (7.26) следует, что:

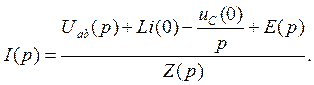                     (7.25)

где 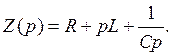-  операторное сопротивление участка цепи между точками а и b . Структура его аналогична структуре комплекса сопротивления того же участка цепи переменному току, если /со заменить на р.

Как указывалось ранее, комплексное число р = a - jb может быть записано в виде р = j ( b — ja ) = j Ω, где Ω = b - ja - комп­лексная частота; Z ( p ) = Z ( j Ω) - сопротивление, оказываемое рас­сматриваемой цепью воздействию U е^{jΩ t -} = U е ^pt, подобно тому как Z ( jω ) есть сопротивление, оказываемое воздействию U е^{jΩ t .}  Поэтому Z ( p ) называют сопротивлением на комплексной частоте.

Уравнение (7.25) может быть названо законом Ома в оператор­ной форме для участка цепи, содержащего ЭДС. Оно записано при ненулевых начальных условиях.

Слагаемое Li (0) представляет собой внутреннюю ЭДС, обуслов-

ленную запасом энергии в магнитном поле индуктивной катушки вследствие протекания через нее тока i (0) непосредственно до ком­мутации. Слагаемое u _с (0)/р представляет собой внутреннюю ЭДС, обусловленную запасом энергии в электрическом поле конденсатора вследствие наличия напряжения на нем u _с (0) непосредственно до коммутации.

В соответствии с формулой (7.25) на рисунке.7.4 изображена операторная схема замещения участка цепи рис. 7.3. Операторные сопротивления ее R , pL , 1 /(Ср). Как следует из формулы (7.25), внутренняя ЭДС Li (0) направлена согласно с направлением тока

i (р), внутренняя ЭДС U_с(0)/р - встречно току i (р).

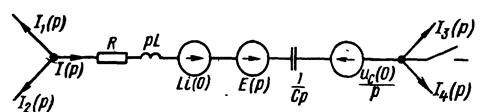
Рисунок 7.4

В частном случае, когда на участке а b отсутствует ЭДС e ( t ) и к моменту коммутации i (0) = 0 и и_с(0) = 0, уравнение(7.25) приобре­тает более простой вид:

I ( p )= U_ab ( p )/ Z ( p ) .            (7.26)

Уравнение (7.26) есть математическая запись закона Ома в опе­раторной форме для участка цепи, не содержащего источник ЭДС при нулевых начальных условиях.