Метод пространства состояний (метод переменных состояния) представляет собой упорядоченный способ нахождения состояния системы в функции времени, использующий матричный метод решения системы дифференциальных уравнений первого порядка, записанных в форме Коши (в нормальной форме). Применительно к электрическим Цепям под переменными состояния понимают величины, определяющие энергетическое состояние цепи, т. е. токи через индуктивные элементы и напряжения на конденсаторах. Значения этих величин полагаем известными к началу процесса. Переменные состояния в обобщенном смысле назовем х. Так как это некоторые функции времени, то их можно обозначить x ( t ).

Пусть в системе п переменных состояния. Матрицу-столбец пе­ременных состояния в n-мерном пространстве состояний обозначим:

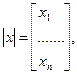,m выходных величин (токи, напряжения) обозначим у,

матрицу-столбец выходных величин 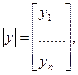 Источники воздействий (источники ЭДС и тока) будем именовать z . Матрица-столбец источников воздействий: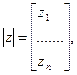

Для электрических цепей можно составить матричный уравне­ния вида:

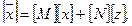                                                          (7.50)

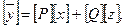                                                            (7.51)

где [М ], [ N ], [Р], [ Q ] - некоторые матрицы, определяемые структу­рой цепи и значениями ее параметров.

На основании принципа наложения решение (7.50)

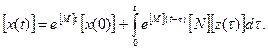                                            (7.52)

где [х(0)] - матрица начальных значений х.

Первое слагаемое в формуле (7.52) описывает свободные про­цессы в системе, второе - принужденные и свободные при нулевом исходном состоянии [вывод формулы (7.52) далее].

Из (7.51) и (7.52) находим:

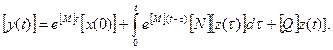                         (7.53)

Поясним формулу (7.52) на простом примере. Ток в схеме рисунка 14 до коммутации был i (0_) = E /(2 R ). Уравнение состояния для этой схемы:

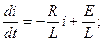
т. е.:

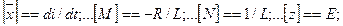
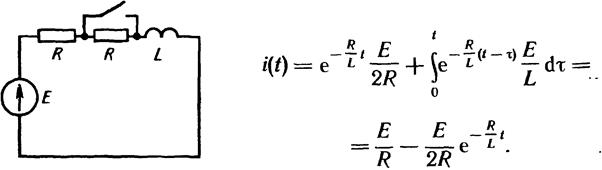
Рисунок 14

Матричную функцию 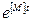 в формуле (7.52) вычисляют по формуле (теореме) Сильвестра:

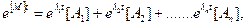            (7.54)

где

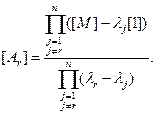                                       (7.55)

λ r - собственные значения (характеристические числа) квадратной матрицы [М ], т. е. корни уравнения:

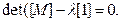                                           (7.56)

Из уравнения (7.56) следует, что уравнение относительно λ со­ставляют, приравнивая нулю определитель матрицы [М], в котором все элементы этой матрицы a_mtn ( m = 1,..., n), расположенные по главной диагонали, заменяют на элементы а_тт - λ .

Характеристические числа λ  - это не что иное, как корни ха­рактеристического уравнения послекоммутационной схемы. Запись решения в виде ряда (7.53) предполагает, что все характеристические числа различны (нет кратных корней). Если же среди корней уравнения det ([ M ] - λ[1]) = 0 будет кратный корень λ _s кратности s, то составляющая e ^{[ M ] t}, обусловленная этим корнем, имеет вид:

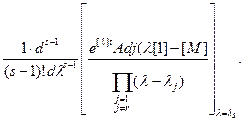                                       (7.57)

где Adj (λ[1] – [ M ]) - присоединенная матрица к матрице λ[1] - [М]. В ней все элементы a_tj заменены на алгебраические дополнения, а затем проведено транспонирование. Составляющие решения по формуле (7.57) соответствуют части решения по формуле разложения, учитывающей кратные корни. При машинном счете функцию e ^{[ M ] t} подсчитывают разложением в ряд:

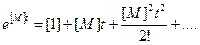
Дополняющие двухполюсники.

Два двухполюсника, содержащие элементы R , L , С, называют дополняющими, если входное сопротивление при их последовательном (параллельном) соединении оказывается чисто активным, не зависящим от комплексной частоты р. Так, двухполюсник из параллельно соединенных L и R ₂ и двухполюсник из параллельно соединенных С и R ₁, (рисунок 15, а) являются дополняющими при их последовательном соединении и выполнении условия R_l = R ₂ = R = .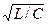

Двухполюсники R ₂ , C , R _{1 t} L при их параллельном соединении (рисунок 15, б) являются дополняющими при том же условии.

Элементы двух дополняющих двухполюсников взаимно дуальны. Элементам L_{l ,} C_{l ,} R ₁ одного соответствуют такие дуальные элементы С₂, L ₂ , R ₂ дополняющего, что произведение сопротивлений двух взаимно дуальных элементов должно быть равно R², где R - произвольное активное сопротивление.

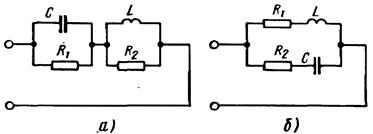
Рисунок 15

Последовательное соединение L ₁ и С₁ в исходном двухполюснике заменяют на параллельное соединение C ₂ = L_l / R ² и L ₂ = C ₁ / R ² в дополняющем. Параллельное соединение С₁ и L ₁, в исходном двухполюснике заменяют на последовательное соединение L ₂ = C ₁ R ² и C ₂ = L ₁ / R ² в дополняющем.