Из курса математики известно, что дробь:

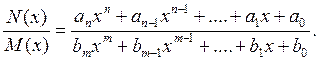           (7.33)

при условии, что п < m и полином М(х) = 0 не имеет кратных корней, может быть представлена в виде суммы простых дробей:

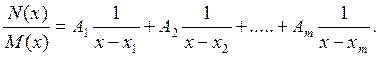           (7.34)

или

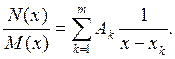
где x_k -  корни уравнения М(х) =0.

Для определения коэффициента А₁ умножим обе части уравнения (7.34) на (х-х₁). В результате получим:

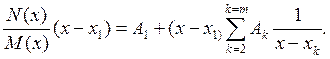                (7.35)

Рассмотрим выражение (7.35) при х→х₁. Правая часть уравнения равна А_1, а левая представляет собой неопределенность, так как множитель ( x – x ₁ ) при х→х₁ равен нулю и знаменатель М(х) при х = х₁ также равен нулю [x ₁ есть корень уравнения М(х) = 0]. Раскроем неопределенность по правилу Лопиталя. С этой целью производную от числителя разделим на производную от знаменателя и найдем предел дроби:

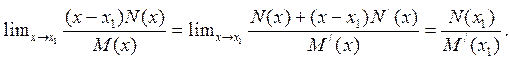
где М'(х) - производная от М(х) по х. М'(х) -  значение М'(х) при х= x ₁ ; N ^/ ( x ₁ ) - значение N ( x) при х = х₁.

Следовательно, из (7.35) при х→х₁ получаем уравнение:

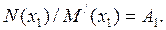                (7.36)

или

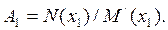                (7.37)\

Аналогично:

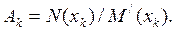                (7.38)

Таким образом:

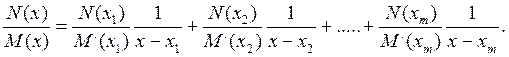(7.39)

или

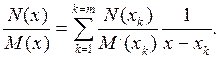                    (7.40)

Формула разложения.

Переход от изображения N ( p )/ M ( p ) к функции времени часто производят с помощью формулы

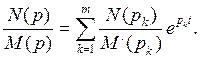                    (7.41)

Которую называют формулой разложения.

Левая часть формулы является функцией р, правая часть - соответствующей ей функцией времени t .

Вывод формулы можно осуществить следующим образом. Пусть изображение какой-либо функции времени, например тока, I(р) = N ( p )/ M ( p ).

Для получения тока как функции времени i ( t ) представим сна­чала N ( p )/ M ( p ) в виде суммы простых дробей - разложим

N ( p ) / M ( p )- С этой целью в формуле (7.40) заменим х на р:

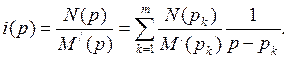                    (7.42)

Перейдем от изображения к оригиналу. Оригиналом левой части является i ( t ). Оригинал правой части равен сумме оригиналов ее слагаемых.

Учтем, что множители N ( p_k )/ M '( p_k ) у слагаемых суммы правой части (7.42) есть постоянные числа (не функции р). Кроме того, функциями р в правой части являются только множители I /(р - p_k ) им соответствуют функции времени вида е^р _k ^t. Поэтому:

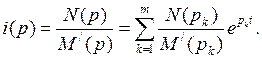                    (7.43)

Переход от изображения (функции р) к оригиналу (функции t ) с помощью формулы разложения (7.43) основан на том, что изображение представлено в виде суммы простых дробей 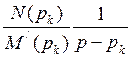, а оригиналами их являются показательные функции .

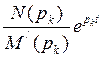Число слагаемых 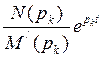равно числу корней уравнения

M (р) = 0. Коэффициенты N ( p_k )/ M '( p_k ) можно сопоставить с постоянными интегрирования дифференциального уравнения (уравнений) цепи в классическом методе расчета.

Если среди корней уравнения М(р) = 0 есть нулевой корень (р = 0), то ему в правой части уравнения (7.43) соответствует слагаемое 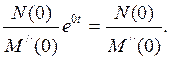Слагаемое  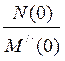представляет собой составляющую искомого тока (напряжения), обусловленную постоянными вынуждающими силами. Если постоянных вынуждающих сил в схеме нет, то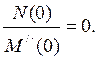

Важно сделать некоторые замечания к формуле (7.43).

1. Формула разложения применима при любых начальных условиях и при любых практически встречающихся формах напряжения источника ЭДС или тока, воздействующего на схему.

2. Если начальные условия не нулевые, то в состав N ( p ) войдут внутренние ЭДС.

3. Если уравнение М(р) = 0 имеет комплексно-сопряженные корни, то слагаемые, соответствующие им в формуле (7.43), оказываются также комплексно-сопряженными и в сумме дают действительное слагаемое.

4. Если воздействующая на схему ЭДС синусоидальна: E_m sin (ω t +ᴪ) и изображение ЭДС взято в виде 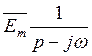, где комплексная амплитуда 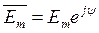,то при использовании формулы разложения из правой части ее для перехода от комплекса к мгновенному значению следует взять коэффициент при j (взять мнимую часть). В соответствии с этим внутренние ЭДС, которые появляются в правой части формулы разложения при ненулевых начальных условиях в цепях с синусоидальной ЭДС должны быть умножены на коэффициент j.

Умножить внутренние ЭДС на j необходимо потому, что только в этом случае наличие этих ЭДС будет учтено при взятии мнимой части от правой части формулы разложения. В цепях с постоянной ЭДС внутренние ЭДС умножать на j не нужно.

5. Если воздействующее на схему напряжение синусоидально, то принужденная составляющая решения входит в число слагаемых 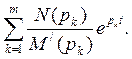и определяется корнем p = jω. Вычисление при­нужденной составляющей в виде члена этой суммы, соответствующего корню p = jω, для сложных схем в большинстве случаев более громоздко, чем непосредственное вычисление ее с помощью симво­лического метода. Поэтому для сложных схем переменного тока принужденную составляющую рекомендуется вычислять символическим методом.

С помощью формулы, подобной формуле (7.43), можно определять не только токи и напряжения, но и многие другие функций времени: заряд конденсатора, скорость перемещения какого-либо тела механической системы и т. п.