Пусть напряжение u ( t ) изменяется во времени по сложному закону, например в соответствии с рисунок 9, б. Начальное напряжение равно и(0). В интервале от t = 0 до t = t ₁ напряжение плавно растет, и закон его изменения и₁(t ). В момент t = t ₁ оно меняется скачком от и_а до и_ь, а затем снова плавно растет, но уже по другому закону u ₂ ( t ) во времени. При t = t ₂ напряжение скачком уменьшается от и_с до нуля.

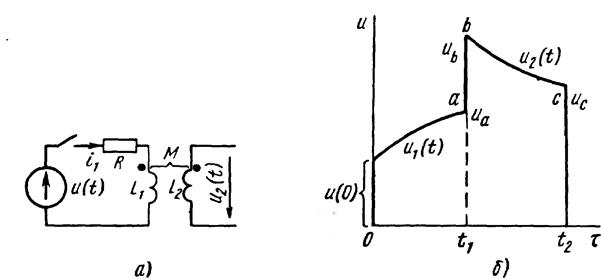
Рисунок 9

Требуется найти ток в каждом из трех интервалов времени. Под первым интервалом будем понимать интервал времени от

t = 0 до t = t ₁ (не включая скачка напряжения от и₂ до и _b ) под вторым - от t ₁ до t ₂ , включая скачок от и_а до и_b, но не включая скачок от и_с до 0; под третьим - при t > t ₂, включая скачок от и_с до 0.

Интегрирование по-прежнему проводим по τ, понимая под t фиксированный момент времени, в который требуется найти ток. На основании принципа наложения ток в любой момент времени t определится как сумма токов от всех напряжений, воздействовавших на цепь до момента t .

В первый интервал времени:

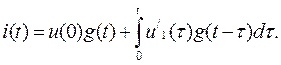
Во второй интервал времени:

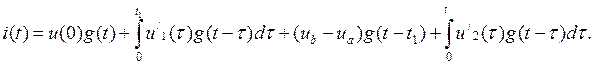
где слагаемое ( u_b - u_a ) g ( t – t ₁ ) обусловлено скачком напряжения и u_a в момент времени t ₁ .

В третий интервал времени:

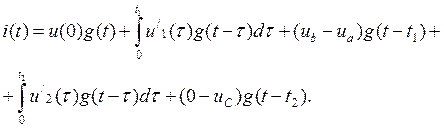
7.32. Сравнение различных методов расчета переходных про цессов.

Классический и операторный методы расчета теоретически можно применять для решения задач любой сложности. Каким из них пользоваться, во многом зависит от навыка и привычки.

Однако классический метод более физически прозрачен, чем операторный, в котором решение уравнений во многом формализовано.

Если при сравнении методов исходить из объема вычислительной работы, то решение уравнений первого, второго, а иногда и третьего порядков для источников постоянной (синусоидальной) ЭДС или тока целесообразно проводить классическим методом, а решение уравнений более высоких порядков - операторным. Объ­ясняется это тем, что чем выше порядок характеристического уравнения, тем более громоздкой и трудоемкой оказывается операция нахождения постоянных интегрирования в классическом методе. Операторный метод имеет перед классическим явное преимущество при решении задач, в которых определение принужденной компоненты искомой величины оказывается затруднительным вследствие сложного характера вынуждающей силы, а также при решении уравнений в частных производных.

Если воздействующее напряжение изменяется во времени, например линейно или в виде всплеска одной или нескольких экспонент, рекомендуется применять операторный метод или интеграл Дюамеля. Но основной областью применения интеграла Дюамеля являются случаи, когда напряжение изменяется по сложному закону во времени, например при наличии скачков напряжения, или когда переходная проводимость g ( t ) и (или) воздействующее на схему напряжение заданы графически (в последнем случае интеграл Дюамеля берется путем численного интегрирования).

Классический и операторный метод, а также метод пространства состояний в аналитической форме и интеграл Дюамеля имеет общий недостаток: необходимость определения всех корней характеристического уравнения, что для уравнений высоких степеней (например, 5,6,7-й,...)требует много времени.

В этих случаях может быть рекомендовано числовое решение на ЭВМ уравнений, составленных по методу пространства состояний; может быть применен и спектральный метод в том виде, в каком он рассмотрен, например, ^в гл. 9. Кроме того, в этих случаях используют моделирующие уста­новки.

7.33. Дифференцирование электрическим путем.

Для четырехполюсников рисунок 10, а, б при определенных условиях выходное напряжение и₂(t ) пропорционально производной от входного напряжения и₁(t), т. е. и₂ ( t ) = du ₁ ( t )/ dt. Схему рисунок 10, а применяют чаще схемы рисунка 10, б, так как при практическом осуществлении она обладает меньшими габаритами, массой и более удобна при регулировке.

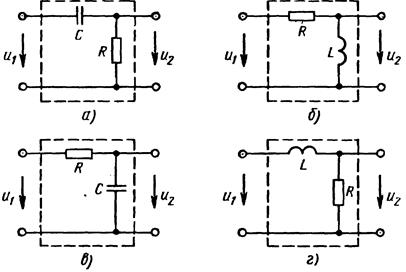
Рисунок 10

Если u ₁ ( t ) , и то du ₁ ( t )/ dt == pU ₁ ( p ). Отсюда следует, что

четырехполюсник осуществляет дифференцирование, если для не-

го U ₂ ( p )= p U ₁ ( p ) . Для схемы рисунка 10, a 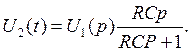Чтобы схема осуществила дифференцирование, необходимо выполнить условие 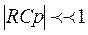|#С/?]<3<1, тогда 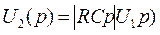U ^ p ) « RCp U_x (р). Для синусоидального процесса заменим р на jω и тогда схема рисунок 10, а будет выполнять свои функции, если .

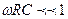Аналогично, доказывается, что для схемы рисунка 10, б необходимо выполнить условие 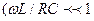. Если u ₁ ( t ) - несинусоидальная периодическая функция, то эти условия должны выполняться для наивысшей частоты функции u ₁ { t ). 

При дифференцировании импульсных воздействий длительно­стью t _И параметры схем рисунка 10, а, б должны удовлетворять усло- виям RC <˂ t _И  и L / R  ˂ < t _И. Эти условия получим из двух предыдущих, если в первом приближении будем считать, что поступление на вход четырехполюсника импульса длительностью t _И соответствует воздействию на вход одной полуволны синусоиды частотой

ω = 2π/ ( t _и ) = π// t _и .