Для перехода от изображения F ( p ) к функции времени f ( t ) может быть использовано обратное преобразование Лапласа:

                                 (a)

Функция F ( p ) аналитична в области Re p > v и стремится к нулю при р →∞. При практическом использовании этой формулы интеграл по бесконечной прямой, параллельной оси ординат, заменяют контурным интегралом, охватывающим все полюсы функции:

                                 (б)

Полюсами называют значения р_у при которых F ( p ) обращается в бесконечность. В том случае, когда F ( p ) = N ( p )/ М(р), полюсами являются корни уравнения М(р) = 0. В теории функций комплекс* ного переменного доказывается, что правая часть формулы (б) рав» на сумме вычетов (Res) подынтегральной функции во всех ее полю­сах, т. е.

Вычетом функции в некотором полюсе называют величину, на которую уменьшается разделенный на 2л/ контурный интеграл от этой функции, когда контур при его стягивании пересечет этот по-

люс. Но вычет функции  в простом полюсе p_k равен

Поэтому:

Таким образом, используя обратное преобразование Лапласа, вывели формулу разложения (7.43).

Запишем формулу разложения при наличии кратных корней. Положим, что уравнение М(р)= 0 имеет q простых корней (р₁„ р₂,..., р _q), корень р _r кратности r и корень p_s кратности s . Тогда:

Переходная проводимость.

Ранее указывалось, что ток в любой ветви схемы может быть представлен в виде произведения напряжения U на входе схемы на собственную или взаимную проводимость g : i = Ug .

При переходных процессах это соотношение также имеет силу. Если на вход какой-либо цепи в момент t = 0 включается постоянное напряжение U (ЭДС Е), то ток i ( t ) в любой ветви этой схемы равен произведению постоянного напряжения U на проводимость g ( t):

i ( t )= Ug ( t).                          (7.45)

При переходном процессе проводимость является функцией времени, поэтому в скобках указывается время t ; g ( t ) называют

переходной проводимостью. Она измеряется в тех же единицах (См), что и обычная проводимость.

Если в формуле (7.44) принять U = 1 В, то i ( t ) = g ( t ), т. е. переходная проводимость какой-либо ветви схемы численно равна току i ( t ) в этой ветви при подключении цепи к источнику постоянно­го напряжения в 1 В. Индексы у g ( t ) указывают на то, какую именно переходную проводимость имеют в виду. Если индексы одинаковы, то имеют в виду собственную переходную проводимость ветви, но­мер которой соответствует цифре, указанной в индексе; если индек­сы разные, то - проводимость между теми ветвями, номера которых указаны в индексе. Например, если источник постоянного напряжения V при нулевых начальных условиях включают в первую ветвь, то ток первой ветви i ₁(t) = Ug ₁₁(t), а ток третьей ветви

Переходную проводимость можно определить расчетным либо опытным путем. При расчете g_kk ( t ) классическим или операторным методом ток k-ветви находят при включении источника постоянного напряжения в /г-ветвь; g_kk ( t ) ток &-ветви вычисляют при включении источника постоянного напряжения U в m-ветвь. Далее, в полученных формулах полагают U = 1 В. При опытном определении переходной проводимости ток i ( t ) соответствующей ветви находят путем осциллографирования.

Ранее было доказано, что g_km = g_mk Это свойство вытекает из симметрии определителя относительно главной диагонали.

Аналогично можно доказать, что операторное изображение проводимости g_km (р) равно операторному изображению g_mk (р). Но если равны изображения двух переходных проводимостей, то равны и сами переходные проводимости, т. е. g_km ( t )= g_mk ( t ).

Данное равенство свидетельствует о том, что на переходные процессы распространяется теорема взаимности. Для переходных процессов теорема взаимности формулируется следующим образом (см. «скелетные» схемы рисунка 7.7): в любой линейной электрической цепи ток переходного процесса k-ветви i_k ( t ), вызываемый включением источника ЭДС e_m ( t ) в m-ветвь (рисунок 7.7, а), равен току переходного процесса i_m ( t ) в m-ветви, вызываемому включением источника ЭДС e_k ( t ) в k-ветвь (рисунок 7.7, б), при условии, что e_k (t) = е_т ( t ).

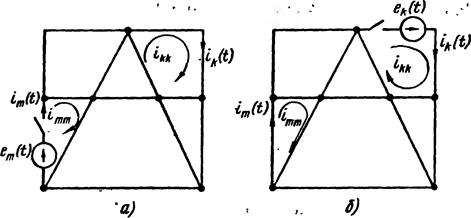
Рисунок 7.7