Расчет операторным методом состоит из двух основных этапов:

1) составления изображения искомой функции времени;

 2) перехода от изображения к функции времени.

7.22. Изображение функции времени в виде отношения N (р)/М(р) двух полиномов по степеням р.

Для тока I (р), если принять Е(р) =Е/р, получим:

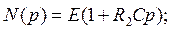
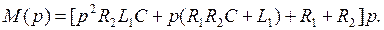
Если же в принять 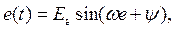 то:

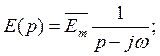 и

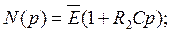
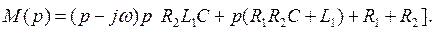
Обозначим высшую степень оператора р в полиноме N ( p ) через п, а высшую степень р в полиноме М(р) - через т.

Часть корней уравнения М(р) =0 обусловлена характером из­менения во времени возмущающей силы, воздействующей на систе­му; остальные корни обусловлены свойствами самой цепи, ее кон­фигурацией и значениями параметров.

Если исключить из рассмотрения сверхпроводящие электриче­ские цепи, то во всех физически осуществимых электрических цепях при воздействии любых ЭДС всегда п < т. Лишь для физически неосуществимых электрических цепей степень п может оказаться равной т. Пример цепи, для которой степень n равна степени т, дан на рисунке7.6.

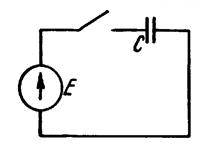
Рисунок 7.6

Если считать, что сопротивление проводов и внутреннее сопротивление источника нулевые, то:

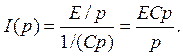
Переход от изображения к функции времени.

Вторым этапом расчета переходных процессов с помощью операторного метода является переход от изображения к функции времени. Эту операцию можно осуществить различными путями.

Первый путь состоит в применении формул соответствия между функциями оператора р и функциями времени t . Часть формул соответствия приведена ранее. В научной литературе имеются специальные исследования, содержащие большое число формул соответствия (1518), охватывающих все возможные практические задачи. Формулами соответствия рекомендуется пользоваться в том случае, когда среди корней уравнения М(р) = 0 есть несколько одинаковых (кратные корни).

Второй путь состоит в применении так называемой формулы разложения. Формула разложения выведена, исходя из предложения, что уравнение М(р) = 0 не имеет кратных корней (при наличии кратных корней формула разложения записывается иначе).

Третий путь - непосредственное применение формулы обрат­ного преобразования Лапласа с использованием теории вычетов.

Формулой разложения широко пользуются на практике, и ее принято рассматривать как основную формулу для перехода от изображения к функции времени.

Рассмотрим два примера на применение формул соответствия, а затем - после рассмотрения вопроса о разложении сложной дроби на простые - перейдем к выводу формулы разложения.