Операторный метод тоже основан на использовании понятия об изображении функций времени. В операторном методе каждой функции времени соответствует функция новой переменной, обозначаемой буквой р и наоборот - функции переменной р отвечает определенная функция времени.

Переход от функции времени к функции р осуществляют с помощью преобразования (прямого) Лапласа.

Таким образом, операторный метод расчета переходных процессов представляет собой метод расчета, основанный на преобразовании Лапласа.

Операторный метод позволяет свести операцию дифференцирования к умножению, а операцию интегрирования - к делению. Это облегчает интегрирование дифференциальных уравнений.

4.8. Преобразование Лапласа.

Условимся под р понимать комплексное число:

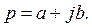                                           (7.10)

где а - действительная, a jb - мнимая части комплексного числа (в ряде книг вместо буквы р пишут s).

В дальнейшем в соответствии с установившейся практикой ко- эффициент b с учетом знака условимся называть не коэффициентом при мнимой части комплекса (чем он в действительности является), а мнимой частью. Функцию времени (ток, напряжение, ЭДС, заряд) обозначают f ( t ) и называют оригиналом. Ей соответствует функция F ( p), называемая изображением, которая определяется следующим образом:

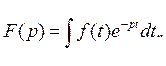                          (7.10а)

Соответствие между функциями F ( p ) и /(/) записывают так:

F ( p ) == f ( t ).                    (7.11)

Знак «==» называют знаком соответствия.

Верхний предел интеграла (7.10а) равен бесконечности. Интегралы с бесконечным верхним пределом называют несобственными. Если в результате интегрирования и подстановки пределов получают конечное число (не бесконечность), то говорят, что интеграл сходится.

В курсе математики доказывается, что интеграл (7.10а), в состав которого входит функция 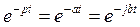, сходится только в том случае, когда модуль функции f ( t ), если и увеличивается с ростом t, то все же медленнее, чем модуль функции 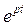, равный e^at .

Практически все функции f ( t ), с которыми имеют дело в курсе ТОЭ, этому условию удовлетворяют.

Составим изображения некоторых простейших функций.

Изображение постоянной.

Требуется найти изображение функции f ( t ) = А, где А - постоянная величина. С этой целью, в (7.10а) вместо f ( t ) подставим А и проведем интегрирование:

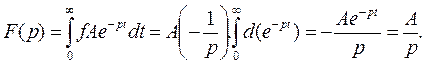
Следовательно, изображение постоянной равно постоянной, де­ленной на р:

A == A / p.                                      (7.12)

7.10. Изображение показательной функции е^{α t} .

Вместо f ( t ) в (7.10а) подставим е^αt:

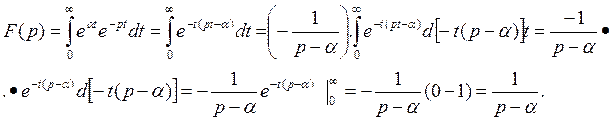    Таким образом,

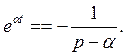                                (7.13)

При выводе формулы (7.13) (при подстановке пределов) было учтено, что действительная часть оператора р больше, чем а, т. е. а > a. Только при этом условии интеграл сходится.

Из формулы (7.13) вытекает ряд важных следствий. Положив в ней α = jω, получим:

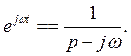                                (7.14)

Формула (7.14) дает возможность найти изображение комплек­са синусоидального тока:

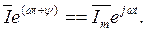
С этой целью обе части (7.14) умножим на постоянное число :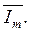

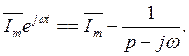                        (7.15)

Аналогично, изображение комплекса синусоидального напря­жения:

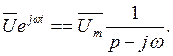                             (7.16)

Функции е^-аt соответствует изображение 1 /(р + α):

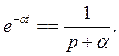                                     (7.17)