На практике встречаются схемы, переходные процессы в которых состоят как бы из двух стадий резко различной продолжительности. Длительность первой стадии в тысячи и мил­лионы раз короче второй. В течение первой стадии токи в индуктив­ных элементах и напряжения на конденсаторах изменяются на­столько быстро (почти скачкообразно), что если считать t = 0_ началом, a t = 0₊ - окончанием первой стадии, то создается впе­чатление, что при переходе от t = 0_ к t = 0₊, т. е. за время, например, в несколько микросекунд, как бы нарушаются законы коммутации.

Для иллюстрации нарушения второго закона коммутации рас­смотрим переходной процесс в схеме рисунка 7.1 с начальными условиями и_С1(0_) = E, и_С2(0_) = 0.

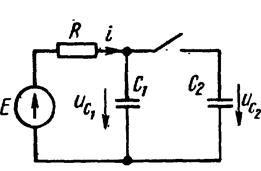
Рисунок 7.1

Сначала при замыкании ключа через конденсаторы возникают очень большие броски токов (ограничиваемые хотя и очень малыми, но все же конечными сопротивлениями соединительных проводов R _пр), прохождение которых приводит почти к мгновенному уравне­нию напряжения на конденсаторах до значения, меньшего Е. (Строго говоря, если учесть сопротивление R _пр, то для первой стадии переходного процесса в схеме рисунка 7.1 характеристическое уравнение будет уравнением второго порядка, один корень которого пру R_np -→ 0 стремится к бесконечности.)

После этого начинается вторая стадия, когда параллельно сое­диненные конденсаторы относительно медленно заряжаются до на­пряжения Е. Длительность переходного процесса практически оп­ределяется второй стадией.

В качестве примера нарушения первого закона коммутации рассмотрим переходной процесс в схеме рисунка 7.2. Быстрое размыкание ключа в первой ветви, например за 10^-5 с, приводит к тому, что сопротивление этой ветви быстро увеличивается, ток i ₁ почти скачком уменьшается до нуля и почти скачком изменяются токи в остальных ветвях.. Таким образом, за очень малое время порядка 10^-5 с (от t = 0_ до t = 0₊)токи резко изменяются,

а i (0₊) ≠ i (0_); i ₂ (0₊) ≠ i ₂ (0_).

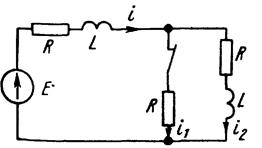
Рисунок 7.2

Нарушение законов коммутации в классической формулировке при переходе от t = 0_ до t = 0₊ объясняется тем, что процессы в быстро протекающей первой стадии и их зависимость от времени не рассматриваются. Если же первую стадию не исключать при рас­смотрении, то ранее рассмотренные законы коммутации выполня­ются.

Для того чтобы можно было рассчитать переходные процессы сразу во второй стадии, как бы перешагнув через первую, надо, во-первых, примириться с тем, что при переходе от от t = 0_ до t = 0₊ в рассматриваемых задачах законы коммутации в классическом виде, , не будут выполнены; во вторых, принять исходные положения, которые позволяют определить значения токов через индуктивности и напряжений на конденсаторах (а если потребуется, то и их производные) при t = 0₊ через значения токов и напряжений при t = 0.. Таких положений (правил) два. При решении задач рассматриваемого типа они заменяют законы (правила) коммутации, в классической формулировке, и потому их называют иногда обобщенными законами (правилами) коммутации.

1- При переходе от t = 0_ до t = 0₊ суммарное потокосцепление 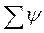 каждого замкнутого контура послекоммутационной схемы не должно претерпевать скачкообразных изменений. Это положение следует из второго закона Кирхгофа и доказывается от противного: если допустить, что  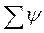некоторого контура изменится скачком, то в уравнении для этого контура, составленном по второму закону Кирхгофа, появилось бы слагаемое  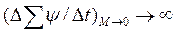и второй закон Кирхгофа не был бы выполнен.

Суммарное потокосцепление представляет собой алгебра­ическую сумму произведений токов ветвей этого контура на индук­тивности их индуктивных элементов (в общем случае с учетом маг­нитной связи с другими ветвями). Со знаком плюс в эту сумму входят слагаемые ветвей, направление токов в которых совпадает с произвольно выбранным направлением обхода контура.

2. При переходе от t = 0_ до t = 0₊ суммарный заряд 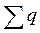 на

обкладках конденсаторов, присоединенных к любому узлу после- коммутационной схемы, должен остаться неизменным. Если этого Че выполнить, то суммарный ток, проходящий через конденсаторы, был  бы бесконечно большим (стремился бы к бесконечности), бесконечно большими были бы токи и через другие ветви, присоединенные к этому узлу. Это также привело бы к нарушению второго закона Кирхгофа.

В заключение обратим внимание на то, что, допустив при пере­ходе от t = 0_ к t = 0₊ скачкообразное изменение токов через ин­дуктивный элемент и скачкообразное изменение напряжений на конденсаторах, тем самым допускаем скачкообразное изменение энергии магнитного поля индуктивных элементов и энергии элект­рического поля конденсаторов.

Суммарная энергия электрического и магнитного полей при t = 0₊ всегда меньше суммарной энергии при t = 0_, так как часть запасенной энергии расходуется на тепловые потери в резисторах, искру при коммутации, электромагнитное излучение в окружающее пространство.

Прежде чем перейти к изучению основ второго метода расчета переходных процессов в линейных электрических цепях - операторного метода, вспомним некоторые известные положения.