Глава 7А
МЕТОДЫ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Общая характеристика методов анализа переходных процессов в линейных электрических цепях.
Расчет переходных процессов в любой линейной электрической цепи состоит из следующих основных операций:
1) выбора положительных направлений токов в ветвях цепи;
2) определения значений токов и напряжений непосредственно до коммутации;
3) составления характеристического уравнения и нахождения его корней;
4) получения выражения для искомых токов и напряжений как функции времени.
Широко распространенными методами расчета переходных процессов являются:
1) Классический, называемый в литературе классическим;
2) операторный метод;
3) метод расчета с помощью интеграла Дюамеля.
Для всех этих методов перечисленные операции (этапы расчета) являются обязательными. Для всех методов первые три операции совершают одинаково и их нужно рассматривать как общую для всех методов часть расчета. Различие между методами имеет место на четвертом, наиболее трудоемком этапе расчета.
Чаще используют классический и операторный методы, реже - метод расчета с применением интеграла Дюамеля. В дальнейшем будут даны сравнительная оценка и рекомендуемая область применения каждого из них.
В радиотехнике, вычислительной и импульсной технике, электронике, автоматике и в технике, связанной с теорией информации, кроме этих трех методов применяют метод анализа переходных процессов, основывающийся на интеграле Фурье. . Для исследования характера переходного процесса, описываемого уравнениями высоких порядков, используют моделирующие установки, а также метод пространства состояний.
Классический метод расчета переходных процессов.
Классическим методом расчета переходных процессов называют метод, в котором решение дифференциального уравнения представляет собой сумму принужденной и свободной составляющих. Определение постоянных интегрирования, входящих в выражение для свободного тока (напряжения), производят путем совместного решения системы линейных алгебраических уравнений по известным значениям корней характеристического уравнения, а также по известным значениям свободной составляющей тока (напряжения) и ее производных, взятых при t = 0+.
Логарифм как изображение числа.
Известно, что для выполнения операций умножения, деления, возведения в степень и извлечения корня из многозначных чисел целесообразно пользоваться логарифмами.
Действительно, операция умножения сводится к сложению логарифмов, операция деления - к вычитанию логарифмов и т. д. Таким образом, произвести расчет легче в силу того, что сравнительно сложная операция сводится к более простой. Каждому числу соответствует свой логарифм, поэтому логарифм можно рассматривать как изображение числа. Так, 0,30103 есть изображение (логарифм) при основании 10 числа 2.
Комплексные изображения синусоидальных функций.
С понятием изображения встречаются также при изучении символического метода расчета цепей синусоидального тока. Согласно символическому методу, комплексная амплитуда есть изображение синусоидальной функции. Так,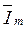 
- изображение синусоидального тока Im sin (ω t + ᴪ ) - Между изображением числа в виде логарифма и изображением синусоидальной функции времени в виде комплексного числа имеется существенная разница. В первом случае речь идет об изображении числа (не функции), во втором - об изображении функции времени.
Подобно тому как введение логарифмов упростило проведение операций над числами, введение комплексных изображений синусоидальных функций времени позволило упростить операции над функциями времени (свести операции расчета цепей синусоидального тока к операциям, изученным ранее).
Изображение постоянной.
Требуется найти изображение функции f ( t ) = А, где А - постоянная величина. С этой целью, в (7.10а) вместо f ( t ) подставим А и проведем интегрирование:
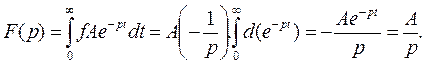
Следовательно, изображение постоянной равно постоянной, деленной на р:
A == A / p. (7.12)
7.10. Изображение показательной функции еα t .
Вместо f ( t ) в (7.10а) подставим еαt:
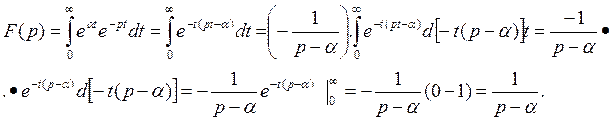Таким образом,
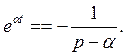(7.13)
При выводе формулы (7.13) (при подстановке пределов) было учтено, что действительная часть оператора р больше, чем а, т. е. а > a. Только при этом условии интеграл сходится.
Из формулы (7.13) вытекает ряд важных следствий. Положив в ней α = jω, получим:
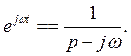(7.14)
Формула (7.14) дает возможность найти изображение комплекса синусоидального тока:
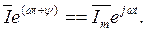
С этой целью обе части (7.14) умножим на постоянное число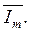 
:
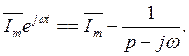(7.15)
Аналогично, изображение комплекса синусоидального напряжения:
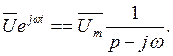(7.16)
Функции е-аt соответствует изображение 1 /(р + α):
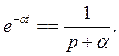(7.17)
Формула разложения.
Переход от изображения N ( p )/ M ( p ) к функции времени часто производят с помощью формулы
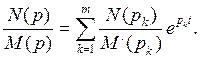(7.41)
Которую называют формулой разложения.
Левая часть формулы является функцией р, правая часть - соответствующей ей функцией времени t .
Вывод формулы можно осуществить следующим образом. Пусть изображение какой-либо функции времени, например тока, I(р) = N ( p )/ M ( p ).
Для получения тока как функции времени i ( t ) представим сначала N ( p )/ M ( p ) в виде суммы простых дробей - разложим
N ( p ) / M ( p )- С этой целью в формуле (7.40) заменим х на р:
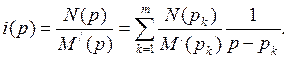(7.42)
Перейдем от изображения к оригиналу. Оригиналом левой части является i ( t ). Оригинал правой части равен сумме оригиналов ее слагаемых.
Учтем, что множители N ( pk )/ M '( pk ) у слагаемых суммы правой части (7.42) есть постоянные числа (не функции р). Кроме того, функциями р в правой части являются только множители I /(р - pk ) им соответствуют функции времени вида ер k t. Поэтому:
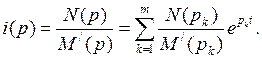(7.43)
Переход от изображения (функции р) к оригиналу (функции t ) с помощью формулы разложения (7.43) основан на том, что изображение представлено в виде суммы простых дробей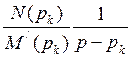 
, а оригиналами их являются показательные функции 
.
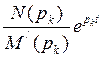Число слагаемых 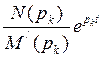равно числу корней уравнения
M (р) = 0. Коэффициенты N ( pk )/ M '( pk ) можно сопоставить с постоянными интегрирования дифференциального уравнения (уравнений) цепи в классическом методе расчета.
Если среди корней уравнения М(р) = 0 есть нулевой корень (р = 0), то ему в правой части уравнения (7.43) соответствует слагаемое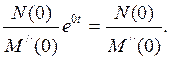 
Слагаемое 
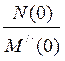представляет собой составляющую искомого тока (напряжения), обусловленную постоянными вынуждающими силами. Если постоянных вынуждающих сил в схеме нет, то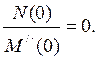 
Важно сделать некоторые замечания к формуле (7.43).
1. Формула разложения применима при любых начальных условиях и при любых практически встречающихся формах напряжения источника ЭДС или тока, воздействующего на схему.
2. Если начальные условия не нулевые, то в состав N ( p ) войдут внутренние ЭДС.
3. Если уравнение М(р) = 0 имеет комплексно-сопряженные корни, то слагаемые, соответствующие им в формуле (7.43), оказываются также комплексно-сопряженными и в сумме дают действительное слагаемое.
4. Если воздействующая на схему ЭДС синусоидальна: Em sin (ω t +ᴪ) и изображение ЭДС взято в виде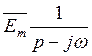 
, где комплексная амплитуда 
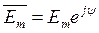,то при использовании формулы разложения из правой части ее для перехода от комплекса к мгновенному значению следует взять коэффициент при j (взять мнимую часть). В соответствии с этим внутренние ЭДС, которые появляются в правой части формулы разложения при ненулевых начальных условиях в цепях с синусоидальной ЭДС должны быть умножены на коэффициент j.
Умножить внутренние ЭДС на j необходимо потому, что только в этом случае наличие этих ЭДС будет учтено при взятии мнимой части от правой части формулы разложения. В цепях с постоянной ЭДС внутренние ЭДС умножать на j не нужно.
5. Если воздействующее на схему напряжение синусоидально, то принужденная составляющая решения входит в число слагаемых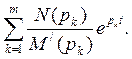 
и определяется корнем p = jω. Вычисление принужденной составляющей в виде члена этой суммы, соответствующего корню p = jω, для сложных схем в большинстве случаев более громоздко, чем непосредственное вычисление ее с помощью символического метода. Поэтому для сложных схем переменного тока принужденную составляющую рекомендуется вычислять символическим методом.
С помощью формулы, подобной формуле (7.43), можно определять не только токи и напряжения, но и многие другие функций времени: заряд конденсатора, скорость перемещения какого-либо тела механической системы и т. п.
Переходная проводимость.
Ранее указывалось, что ток в любой ветви схемы может быть представлен в виде произведения напряжения U на входе схемы на собственную или взаимную проводимость g : i = Ug .
При переходных процессах это соотношение также имеет силу. Если на вход какой-либо цепи в момент t = 0 включается постоянное напряжение U (ЭДС Е), то ток i ( t ) в любой ветви этой схемы равен произведению постоянного напряжения U на проводимость g ( t):
i ( t )= Ug ( t). (7.45)
При переходном процессе проводимость является функцией времени, поэтому в скобках указывается время t ; g ( t ) называют
переходной проводимостью. Она измеряется в тех же единицах (См), что и обычная проводимость.
Если в формуле (7.44) принять U = 1 В, то i ( t ) = g ( t ), т. е. переходная проводимость какой-либо ветви схемы численно равна току i ( t ) в этой ветви при подключении цепи к источнику постоянного напряжения в 1 В. Индексы у g ( t ) указывают на то, какую именно переходную проводимость имеют в виду. Если индексы одинаковы, то имеют в виду собственную переходную проводимость ветви, номер которой соответствует цифре, указанной в индексе; если индексы разные, то - проводимость между теми ветвями, номера которых указаны в индексе. Например, если источник постоянного напряжения V при нулевых начальных условиях включают в первую ветвь, то ток первой ветви i 1(t) = Ug 11(t), а ток третьей ветви
Переходную проводимость можно определить расчетным либо опытным путем. При расчете gkk ( t ) классическим или операторным методом ток k-ветви находят при включении источника постоянного напряжения в /г-ветвь; gkk ( t ) ток &-ветви вычисляют при включении источника постоянного напряжения U в m-ветвь. Далее, в полученных формулах полагают U = 1 В. При опытном определении переходной проводимости ток i ( t ) соответствующей ветви находят путем осциллографирования.
Ранее было доказано, что gkm = gmk Это свойство вытекает из симметрии определителя относительно главной диагонали.
Аналогично можно доказать, что операторное изображение проводимости gkm (р) равно операторному изображению gmk (р). Но если равны изображения двух переходных проводимостей, то равны и сами переходные проводимости, т. е. gkm ( t )= gmk ( t ).
Данное равенство свидетельствует о том, что на переходные процессы распространяется теорема взаимности. Для переходных процессов теорема взаимности формулируется следующим образом (см. «скелетные» схемы рисунка 7.7): в любой линейной электрической цепи ток переходного процесса k-ветви ik ( t ), вызываемый включением источника ЭДС em ( t ) в m-ветвь (рисунок 7.7, а), равен току переходного процесса im ( t ) в m-ветви, вызываемому включением источника ЭДС ek ( t ) в k-ветвь (рисунок 7.7, б), при условии, что ek (t) = ет ( t ).
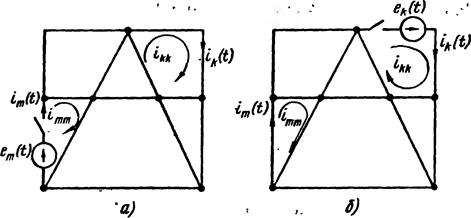
Рисунок 7.7
Интеграл Дюамеля.
Познакомимся с третьим методом расчета переходных процессов в линейных электрических цепях - расчетом с помощью интеграла Дюамеля.
При использовании интеграла Дюамеля переменную, по которой производится интегрирование, обозначим т, а под t по-прежнему будем понимать тот момент времени, в который требуется найти ток в цепи. Пусть к цепи с нулевыми начальными условиями в момент времени t = 0 подключается напряжение u (τ)(рисунок 8).
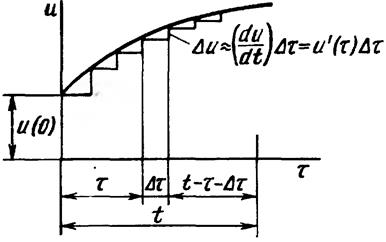
Рисунок 8
Для того чтобы найти ток в цепи в момент времени t , заменим плавную кривую ступенчатой и просуммируем токи от начального напряжения и(0) и от всех ступенек напряжения, вступающих в действие с запозданием во времени.
Напряжение и(0) в момент времени t вызовет в цепи ток
и(0)g( t ) где g (t) - переходная проводимость. В момент времени
τ + Δτ (рисунок 8) возникает скачок напряжения:
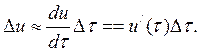
Для того чтобы найти составляющую тока в момент времени t , вызываемую этим скачком напряжения Aw, необходимо и'(τ) Δτ умножить на значение переходной проводимости с учетом времени действия скачка до момента времени t . Из рисунка 8. видно, что это время равно t - τ - Δτ. Следовательно, приращение тока от этого скачка составляет и'( τ)g ( t - τ - Δτ) Δτ.
Полный момент времени t получим, если просуммируем все частичные токи от отдельных скачков и прибавим их к току
u (0) g ( t ):
i ( t ) =и(0 ) g ( t) + Σu /( τ ) g ( t - τ - Δτ ) Δτ.
Число членов суммы равно числу ступенек напряжения. Очевидно, что ступенчатая кривая тем лучше заменяет плавную кри- вую, чем больше число ступенек. С этой целью заменим конечный интервал времени Δτ на бесконечно малый dτ и перейдем от суммы к интегралу:
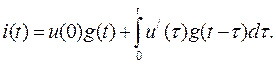(7.46)
Формулу (7.46) называют интегралом Дюамеля.
С помощью интеграла Дюамеля можно найти не только ток, но и любую другую физическую величину, например напряжение. В этом случае в формуле вместо переходной проводимости g(t ) будет входить переходная функция h(t), если на входе цепи действует источник ЭДС (напряжения), и переходное сопротивление R(t ) если на входе цепи действует источник тока.
Дополняющие двухполюсники.
Два двухполюсника, содержащие элементы R , L , С, называют дополняющими, если входное сопротивление при их последовательном (параллельном) соединении оказывается чисто активным, не зависящим от комплексной частоты р. Так, двухполюсник из параллельно соединенных L и R 2 и двухполюсник из параллельно соединенных С и R 1, (рисунок 15, а) являются дополняющими при их последовательном соединении и выполнении условия Rl = R 2 = R =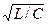 
.
Двухполюсники R 2 , C , R 1 t L при их параллельном соединении (рисунок 15, б) являются дополняющими при том же условии.
Элементы двух дополняющих двухполюсников взаимно дуальны. Элементам Ll , Cl , R 1 одного соответствуют такие дуальные элементы С2, L 2 , R 2 дополняющего, что произведение сопротивлений двух взаимно дуальных элементов должно быть равно R2, где R - произвольное активное сопротивление.
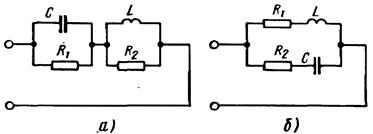
Рисунок 15
Последовательное соединение L 1 и С1 в исходном двухполюснике заменяют на параллельное соединение C 2 = Ll / R 2 и L 2 = C 1 / R 2 в дополняющем. Параллельное соединение С1 и L 1, в исходном двухполюснике заменяют на последовательное соединение L 2 = C 1 R 2 и C 2 = L 1 / R 2 в дополняющем.
Вопросы для самопроверки
1. Дайте определение переходному процессу.
2. Что понимают под принужденными и свободными токами и напряжениями?
3. Сформулируйте законы (правила) коммутации.
4. Дайте определение зависимым и независимым начальным условиям.
5. Какие вы знаете способы составления характеристического уравнения.
6. Объясните, почему при составлении характеристического уравнения путем приравнивания нулю входного сопротивления Z ( p )= N ( p )/ M ( p ) в общем случае нельзя сокращать числитель и знаменатель дроби на общий множитель.
7. Чем определяется число корней характеристического уравнения?
8. Изложите сущность классического метода расчета и принцип составления уравнений для определения постоянных интегрирования.
9. Переходный процесс в некоторой цепи сопровождается биениями. О чем это может свидетельствовать?
10. Дайте обоснование обобщенным законам коммутации.
11. Запишите известные вам соотношения между f ( t ) и F ( p ), а также теоремы операторного метода и предельные соотношения.
12. Почему р называют комплексной частотой?
13. Охарактеризуйте этапы расчета операторным методом.
14. В чем особенности расчета переходных процессов операторным методом при синусоидальном источнике и ненулевых начальных условиях?
15. Охарактеризуйте свойства единичной функции 1(/) и свойства дельта-функции δ( t ).
16. Определите переходную и импульсную переходную проводимости (сопротивления) и функции. Укажите, с какой целью они используются.
17. Охарактеризуйте идею расчета с помощью интеграла Дюамеля.
18. Прокомментируйте известные вам формы записи интеграла Дюамеля.
19. Какими способами можно определить отзвук системы, когда на нее воздействует импульс напряжения или тока?
20. Поясните принцип работы интегрирующих и дифференцирующих цепей. Запишите условия, при которых эти цепи выполняют свои функции.
21. Чем следует руководствоваться при формировании дополняющих двухполюсников?
22. Поясните идею расчета переходных процессов с помощью обобщенных функций.
23. Перечислите основные этапы расчета методом переменных состояния.
24. Как составляют уравнения переменных состояния путем сведения послекоммутационной схемы к чисто резистивной?
25. Охарактеризуйте сильные и относительно слабые стороны известных вам методов расчета переходных процессов.
26. Что понимают под системными функциями? Какие виды чувствительности системных функций вы знаете?
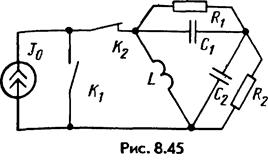
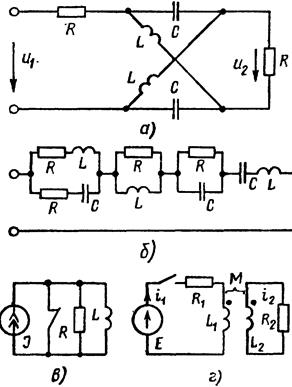
Рисунок 8.46
27. В схеме рисунок 8.45 с источником тока I 0 в момент t = 0 одновременно размыкается ключ K 2 и замыкается K 1. Показать, что заряды, протекшие через сопротивление R 1 и R 2 за время от 0 до ∞, не зависят от емкостей С1 и С2. Определить величины этих зарядов. (Ответ: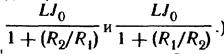 
J29. Покажите, что в симметричной мостовой схеме (рис. 8.46, а), в которой выполняется условие L/C = R 2 , переходная
I -7'
функция h ( t ) = — — + е .
30. В схеме рис. 8.46, 6 R = L = С = 1. Покажите, что
входная переходная проводимость равна te ~ *.
31. Покажите, что энергия, запасаемая в L схемы рис. 8.46, в (начальные условия нулевые), равны тепловым потерям в R .
32. Первичная обмотка трансформатора рис. 8.46, г при нулевых начальных условиях подключается к источнику постоянной ЭДС Е, Rx = /?2 = R; Lx = L2 = М.
Определите ij(0_|_), i2(0_j_). [Ответ i,(0+) = —i2(0+) = E /(2 R ).]
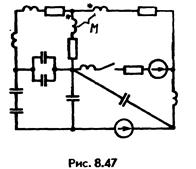
33. Определите степень характеристического уравнения для схемы рис. 8.47.(Огвет — пятая.)
34. Как определить К(р) через h ( t ) и через h (f)?
35. По h ( t) = 4(1 + 2е
ника определите его /((/со). (Ответ: )
36. По К(/со) = „
3 R + /coL _ RC ^ L + /coL
некоторого четырехполюсника определите его h ( t) при R — 0,2 Ом, С = 5 Ф, L = 1 ^Н- (Ответ: h ( t )= 1,62е—°’724* — 0,62е~ 0,276#.)
37. На вход четырехполюсника с
( d /d\"i / d /DT-)
38. В схеме рис. 8.4, в при размыкании ключа происходит переходный процесс. Определить законы изменения во времени напряжений исх и ыс2 на конденсаторах. Задано/(f) = lsin(cof + 90°) A, R = 1/соС = 1 Ом; со = 100 рад/с.
0,253 — 0,15е
(/<■>) = ГТ1Г воздействует единичный импульс напряжения в виде 6-функции 1 -f- /2ш
Определите напряжение на выходе четырехполюсника после окончания действия
импульса. (Ответ: 0,25е 0,5/.)38.
Решите задачи 11.4; 11.12; 11.15; 11.26; 11.29; 11.32; 11.38; 11.40; 11.47; 11.50; 11.55; 11.57.
ПРИЛОЖЕНИЕ 1
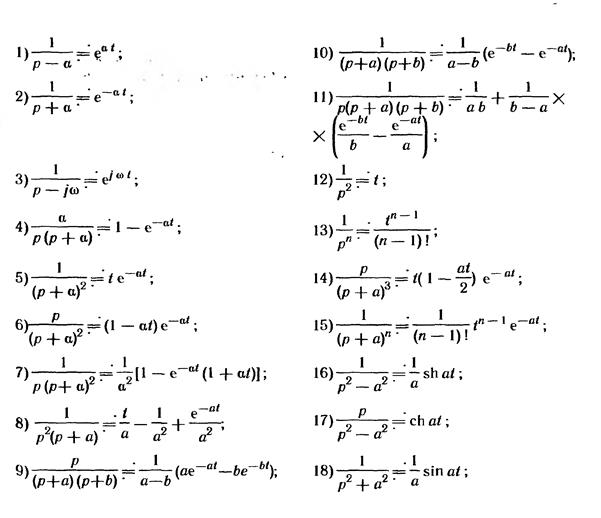
ЗАДАНИЯ
Пример 80.
В схеме рис. 8.17 до замыкания ключа был установившийся режим: R \ ~ R \' = /?з = 50 Ом; С = 100 мкФ; Е — 150 В. Требуется найти: 1) полные, принужденные и свободные составляющие токов i \, *2, /3 и ис при t = 0+, а также
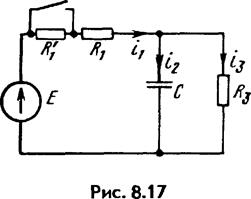
Рисунок -
начальное значение производной от свободного напряжения на конденсаторе; 2)токи t'l, *2, ("з и напряжение ис в функции времени.
Решение первой части задачи. До коммутации «2(0_) = О и ij(0_) = i'3(0_J = E /{ RX + + R 3) — 150/150 = I A.
Напряжение на конденсаторе равно напряжению на резисторе R ^- ис(0_) = 13(0_)/?3 = 1 • 50 = 50 В.
Найдем принужденные значения токов и напряжений после коммутации:
<1„р = 'з,ф = E /( R, + R 3 ) = 150/100 = 1,5 А; мСпр(°+) = W°+>*3 = 1,5 ■ 50 = 75 В.
По второму закону Кирхгофа составим уравнение для контура, образованного первой и второй ветвями при t — 0_|_:
*1(0+)Я| + М°+) = но М°+)= М0-)-
Поэтому
Е — ыс(0_) 150-50
«0+) = —
Из уравнения wc(0+) = *3(0+)/?3 получим
Ф+) = «с(®+)/ Я3 = 1 А.
По первому закону Кирхгофа ^(О^) = + *з(®+)‘ Следовательно,
*2(0+) = 4(0+) - ‘з(°+) = 2 - 1 = 1 А.
Свободные составляющие тока и напряжения при t = 0_|_ определим как разности между полными и принужденными величинами:
“с 0,(0+) = М°+) - “с „Р<°+) = 50 — 75 = — 25 В; i,c„(0+) = '[(О-)-) (1 ,ф(0+) = 2 1,5 = 0,5 А;
HbJf >+) = %№+) - W°+> = 1 - 0 = 1 А; ■'зс»(0+) = Ф+) ~ <злР(0+) = 1 - 1,5 = - 0,5 А.
Так как свободный ток через конденсатор
йис св
*св = С то 6и с = l JC -
В рассматриваемом примере
(<Чсв/<»), = о+ = 'W°+)/C = '/(100.КГ6) = Ю4 В/с.
Решение второй части задачи. Характеристическое уравнение для послекоммутационной схемы pR ^ R ^ C -f- /?, -f- R 3 = 0 имеет один корень
I
' —ад^=-400с
Каждый ток равен сумме принужденной и свободной составляющей Aept, гдеЛ равно значению свободной Составляющей при t — 0_|_ (рис. 8.18):
j, = 1,5 + 0,5е~ 400' A; i 2 = е~ 400< А;
/3 =1,5 — 0,5е“ ти А; ис = 75 - 25е~ 4001 В.
Пример 81.
В схеме рис. 8.19 до замыкания ключа был установившийся режим-
Пример 88. В схеме рис. 8.29 при нулевых начальных условиях замыкают ключ, доставить операторные изображения юков п и /з, пользуясь методом контчрных токов.
Пример 94. Определить юк «'1(0 в схеме рис. 8.17 с помощью формулы разложения и сравнить с результатом решения классическим методом (см. пример 80), если Е = 150 В; R = ЯГ = /?3 = 50 Ом; С = 100 мкФ; ые(0) = 50 В.
Решение. Составим послеком мутационную операторную схему (рис. 8.32), имея в виду, что начальные условия ненулевые. Внутренняя ЭДС «с(0)/р позволяет учесть, что до коммутации конденсатор был заряжен до напряжения ис(0) током ф rum ом у она направлена встречно току /2 (р). Узел 0 схемы заземлим. Потенциал узда / обозначим yi ( p ) и определим ei о по методу узловых потенциалов: о
Мнимую, а недействительную часть из формулы разложения берут потому, чТ° заданная ЭДС £msin(t»< -f- ^) есть мнимая часть комплекса
Пример 101. Найти ii = f ( t ) и ич = f ( t ) при замыкании ключа из схеме рис. 8.37, а.
Напряжение источника ЭДС u ( t ) = 100 (1 — е~а<)В; а = 0,25 с~*; R = 0,5 Ом; Li — = 1 Гн; М = 0,5 Гн.
Решение. Переходная проводимость цепи, состоящей из последовательно
включенных R и L , g ( t ) — — (1 — e ~ bt ), где
R
ь - Я/L,; at ~ 1) = ^l1 - е-‘«-х>].
Первое слагаемое в формуле (8.63) выпадает, так как и (0) = 0. При этом и' (/) = ^7 I00 (1 — e ~ Gt ) = Ю0ае~а<; и' (т) = 100а е-ат;
Пример 107. Путем использования обобщенных функций решить задачу примера 86(см. рис. 8.24).
Решение. В уравнении для послеком мутационной схемы
rfr d"C1 Л Г dUC 2 l Г
At +С2-1Г]+"С1 = £
подставим
u ci = «С1-(0Н- 0 + «ci+(0H0; «сг = «С2-(0Н— 0 + «С2+(*)Ц0;
Глава 7А
МЕТОДЫ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Дата: 2018-11-18, просмотров: 654.
